Memory Addresses and Algorithms

Prelim Module 1

Memory Addresses

The main memory is a a series of endless boxes organized into groups of eight. Each box holds a zero or one. Each group of eight boxes (1 byte) is assigned a unique number called a _

Algorithm

It is a step-by-step procedure, which defines a set of instructions to be executed in a certain order to get the desired output. _ are generally created independent of underlying languages, i.e. It can be implemented in more than one programming language.

Search

(Basic Categories of Algorithm)

• An algorithm to look for an item in a data structure

Sort

(Basic Categories of Algorithm)

• An algorithm to arrange items in a certain order

Insert

(Basic Categories of Algorithm)

• An algorithm to put an item in a data structure

Update

(Basic Categories of Algorithm)

• An algorithm to update an existing item in a data structure

Delete

(Basic Categories of Algorithm)

• An algorithm to erase an existing item from a data structure

Unambiguous

(Characteristics of an Algorithm)

• Each of the algorithm’s steps (or phrases), and their inputs/outputs should be clear and must lead to only one meaning. It should be clear

Input

(Characteristics of an Algorithm)

• An algorithm should have 0 or more well-defined inputs

Output

(Characteristics of an Algorithm)

• An algorithm should have 1 or more well-defined outputs and should match the desired output.

Finiteness

(Characteristics of an Algorithm)

• Algorithms must terminate after a finite number of steps

Feasability

(Characteristics of an Algorithm)

• The algorithm should be feasible with the available resources

Independent

(Characteristics of an Algorithm)

• An algorithm should have step-by-step directions, which should be independent of any programming code.

A Priori Analysis

(Algorithm Analysis)

• This is a theoretical analysis of an Efficiency of an algorithm, it is measured by assuming that all other factors, for example, processor speed, are constant and have no effect on the implementation.

A Posterior Analysis

(Algorithm Analysis)

• This is an empirical analysis of an algorithm. The selected algorithm is implemented using a programming language. This is then executed on the target computer in this analysis, actual statistics like running time and space required, are collected.

Algorithm Complexity

An algorithm analysis deals with the execution or running time of various operations involved.

The complexity of an algorithm f(n) gives the running time and/or the storage space required by the algorithm in terms of n as the size of input data.

Space Complexity

This complexity of an algorithm represents the amount if memory space required by the algorithm in its life cycle.

Time Complexity

This complexity of an algorithm represents the amount of time required by the algorithm to run to completion.

Time requirements can be defined as a numerical function T(n), where T(n) can be measured as the number of steps, provided each step consumes constant time.

Asymptotic Analysis

This analysis of an algorithm refers to defining the mathematical foundation/framing of its run-time performance. Using asymptotic analysis, we can very well conclude the best case, average case, and worst-case scenario of an algorithm.

It mainly refers to computing the running time of any operation in mathematical units of computations. It is input bound.

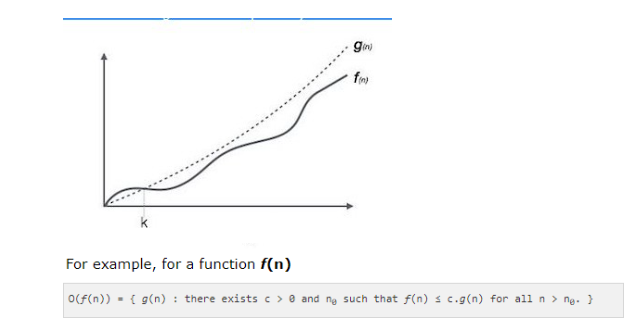
Ο(n) notation

(Asymptotic Notations)

It is the formal way to express the upper bound of an algorithm’s running time. It measures the worst-case time complexity or the longest amount of time an algorithm can possibly take to complete

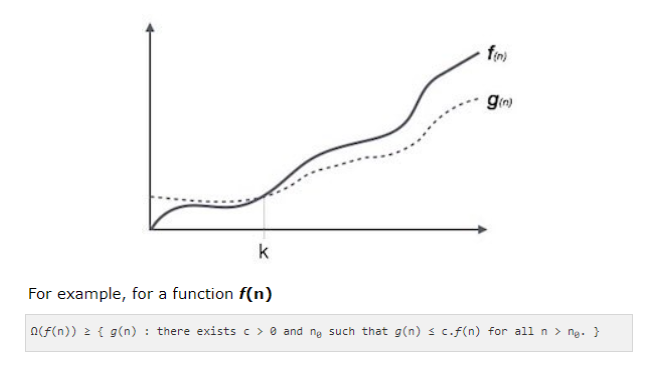
Ω(n) Omega Notation

(Asymptotic Notations)
It is the formal way to express the lower bound of an algorithm’s running time. It measures the best case time complexity or the best amount of time an algorithm can possibly take.

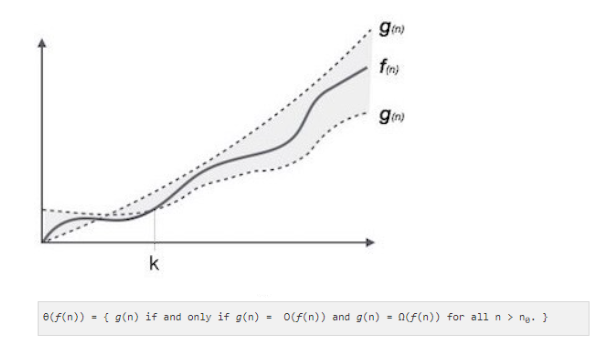
θ(n) Theta Notation

(Asymptotic Notations)
It is the formal way to express both the lower bound and the upper bound of an algorithm’s running time. It is represented as follows:

Arrays

It is a collection of items stored in contiguous memory locations. The idea is to store multiple items of the same type together. This makes it easier to calculate the position of each element by simply adding an offset to a base value, i.e., the memory location of the first element.

It can contain primitives(int, char, etc.) as well as non-primitive reference of class.