Week 10- Invertible Matrices and Determinants

When is the matrix product defined?

If the inner dimensions agree:

(n x k)((k x m)

When is a matrix invertible?

If it is square (n x n)

How do you test for invertibility?

Using the following conditions:

A has n columns.

• To be invertible, L must be one-to-one and onto.

• This means that the kernel of A is just 0, or ker(A) = just {0}, or dim(ker(A)) = 0

• So the rank of A must be n

• So the columns of A must be linearly independent

Algorithm for computing the inverse matrix

If A is an invertible n × n matrix, write the following double-width augmented matrix:

[ A | I_n ].

Use row operations to put this combined matrix into RREF. The resulting matrix will be: [ I_n | A−1 ]

where A−1 is the inverse of A

Determinant

A single scalar value associated with linear transformation L (and its associated standard matrix A)

• The magnitude of D represents the overall scaling done by the transformation.

• The sign of D is related the directional or orientation flips done by the transformation

Computing determinant for 2 × 2 matrices

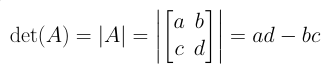
Computing determinant for 2 × 2 matrices

Copy the 1st two columns beside the matrix, then

• Multiply down the diagonals, and up the diagonals as shown, then

• Add the down-right diagonal products, and subtract the up-right diagonals.

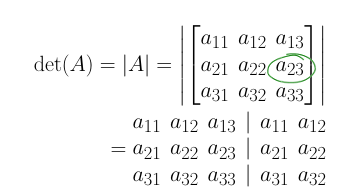
How could you find a perpendicular vector to two 3D vectors?

cross-multiplying two 3D vectors (computing determinant) will produce a vector perpendicular to both

Computing the determinant for n x n matrices

Laplace Expansion Formula:

1. The “checkerboard” pattern of signs. This always starts as a + in the top-left corner, and then alternates for every vertical or horizontal step taken

2. The (n−1)×(n−1) sub-matrix associated with any entry. For any entry aij in an n×n matrix, we make a smaller sub-matrix by crossing out the row i and column j that entry is in.

Formally:

1. Pick any row or column.

2. For every entry aij in that row or column: compute (checkerboard sign) ×(aij)× (det of sub-matrix for aij)

3. Take the sum of all the values from step 2

Determinant in terms of scaling

det(A) represents the scaling effect of A as a transform on areas in R2, volumes in R3

Determinant in terms of invertibility of matrices

det(A)=0 —> A is not invertible

• transform A collapses at least 1 dimension

• ker(A)=/ just {0}

• A is not injective

det(A)=/ 0 —> A is invertible

Determinants when multiplying matrices

B x A matrix product

det(BA) = det(B) x det(A)

Determinants of inverse matrices

det(A) det(A^-1) = det(I_n) —> det(A^-1) = 1/det(A)

Inverse matrices using adjoint matrices

A⁻¹ = 1/det(A)Adj(A) where Adj(A) is a new matrix, based on determinants.

Adj(A) = CT, where:

• The T indicates a transpose, or a reflection of values across the diagonal.

• The C matrix is the cofactor matrix of A, which is defined element-by-element as Cij = (−1)i+j det(Mij), and

• Mij is the sub-matrix of A with row i and column j removed