Trigonometric functions and equations

What is the y = sin x graph?

The graph of y = sin x is a continuous, periodic wave that oscillates between -1 and 1 with a period of 2π, showing a smooth sine wave pattern.

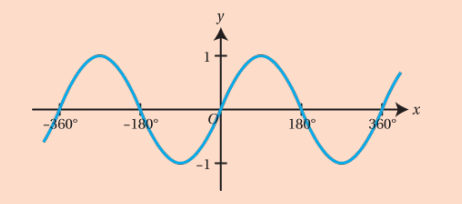
Give the different relationships with the y = sin x graph

sin x = sin (180 - x)

• sin x and sin(180 - x) both give the same y value

• in the unit circle, the first and second quadrants, they both have the same heights for y

sin x = sin(x + 360)

• sine repeats every 360 degrees

sin(180 + x) = sin(-x) = -sin x

• reflection in the x-axis from 180 degrees

What is the graph for cos x?

The graph of y = cos x is a continuous, periodic wave that oscillates between -1 and 1 with a period of 2π, exhibiting a smooth cosine wave pattern.

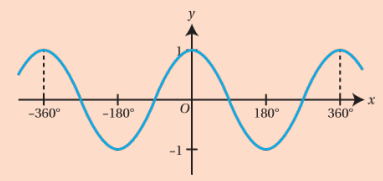
Give the different relationships with the y = cos x graph

cos x = cos (-x)

• symmetry of the graph of cos x about the y-axis

• on the unit circle, x and -x lie on opposite side of the x-axis, but have the same x coordinate

cos x = cos (x + 360)

• cosine repeats every 360

cos (180 - x) = cos (180 + x) = -cos x

• If you reflect a point across 180, the cosine becomes the negative of the original

• symmetry about x = 180, but with a change of sign

What are general graphical relationships between cos x and sin x?

sin x = cos (x + 90) = cos (90 - x)

cos x = sin (x + 90) = sin (90 - x)

What identity combines all the trig functions together?

tan x = sin x / cos x

What is the graph for tan x?

The graph of tan x is a periodic function with vertical asymptotes at odd multiples of ( \frac{\pi}{2} ). It oscillates between negative and positive infinity, with a period of ( \pi ) and crosses the x-axis at multiples of ( \pi ).

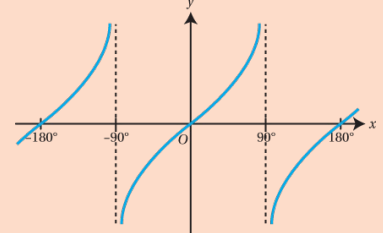
Give the different relationships with the y = tan x graph

tan x = tan (x + 180) = tan (x + 360)

What is the identity that uses sin² x and cos² x?

sin² x + cos² = 1

How would you find the values of x that satisfy sin x = a?

1. find x₁ using sin^-1 a

2. find x₂ by doing 180 - x₁

3. find the other solutions by adding or subtraction 360 by each solution

How would you find the values of x that satisfy cos x = a?

1. find x₁ by doing x₁ = cos^-1a

2. find x₂ by doing x₂ = -x₁

3. find other solution by adding for subtracting 360 to each solution

How would you find the values of x that satisfy tan x = a?

1. find x₁ by doing tan^-1a

2. find other solutions by adding or subtracting 180

Solving trig equations with transformations involved

• make substitution such as A = 2x

• change the interval for x into the interval for A

• solve the equation in the usual way

• transform the solution back into the original variable