5 Meccanica Razionale Capitolo 5: Equilibrio, equazioni cardinali e principio dei lavori virtuali

enunciare il postulato delle reazioni vincolari

ad ogni vincolo agente su un punto materiale P può essere sostituita una forza (reazione vincolare) che realizza lo stesso effetto dinamico del vincolo

scrivere il secondo principio della dinamica per un punto materiale P usando il postulato delle reazioni vincolari

F + Φ = m*a dove Φ è la reazione vincolare

definire l’attrito dinamico

l’attrito è la componente di direzione concorde ma verso inverso alla velocità di un punto materiale che si muove con velocità v in contatto con una superficie.

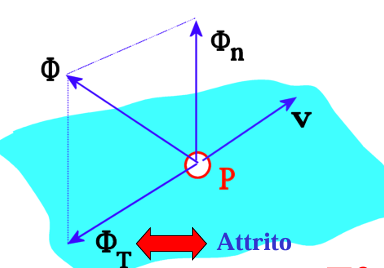
che cosa dice la legge di Coulomb-Morin per l’attrito statico

è una legge che mette in correlazione la forza vincolare tangente al piano (Forza di attrito) e la forza normale al piano. fs è un fattore di attrito tra 0 e 1

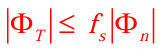
che cosa è l’angolo di attrito dinamico/statico

mette in relazione, come il fattore di attrito dinamico la forza vincolare normale e tangente. rappresenta l’angolo critico di un piano inclinato su qui un blocco scorre con velocità costante, si puo anche vedere come nell’immagine un cono: se la forza vincolare sta in questo cono allora l’attrito è piu grande della forza attiva ed il corpo è in una posizione di equilibrio.
idem per statico

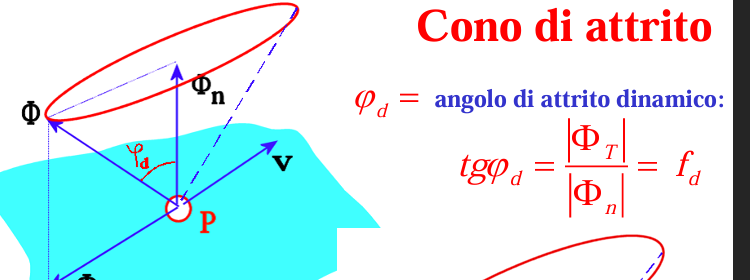
Quale è la definizione di vincoli lisci,

Quali tre tipi di vincoli speciali ci sono
(c’è foto con spiegazione intuitiva)

i vincoli lisci esercitano solo quelle forze il cui lavoro virtuale è non negativo per ogni spostamento virtuale!

ci sono due tipi di vincolo che soddisfano il requisito:

1. vincoli senza attriti, da notare con il disegno se non appena la forza esercitata dal vincolo ha una componente tangente al piano il lavoro puo essere negativo e perciò non è oiu vincolo liscio

2. corpo vincolato da un punto fisso, qui si nota che: δL(v) = Φ × δΩ = 0 perche
   δΩ = 0 dato che nessuno spostamento è concesso

3. vincolo di puro rotolamento: qui deve esistere l’attrito senno un disco non rotolerebbe lungo una curva, ma l’unico punto su cui agisce l’attrito è il punto di contatto che coincide anche con il punto di istantanea rotazione per definizione ha velocità nulla! Anche qui come nel caso 2 δΩ = 0 —> δL(v) =0

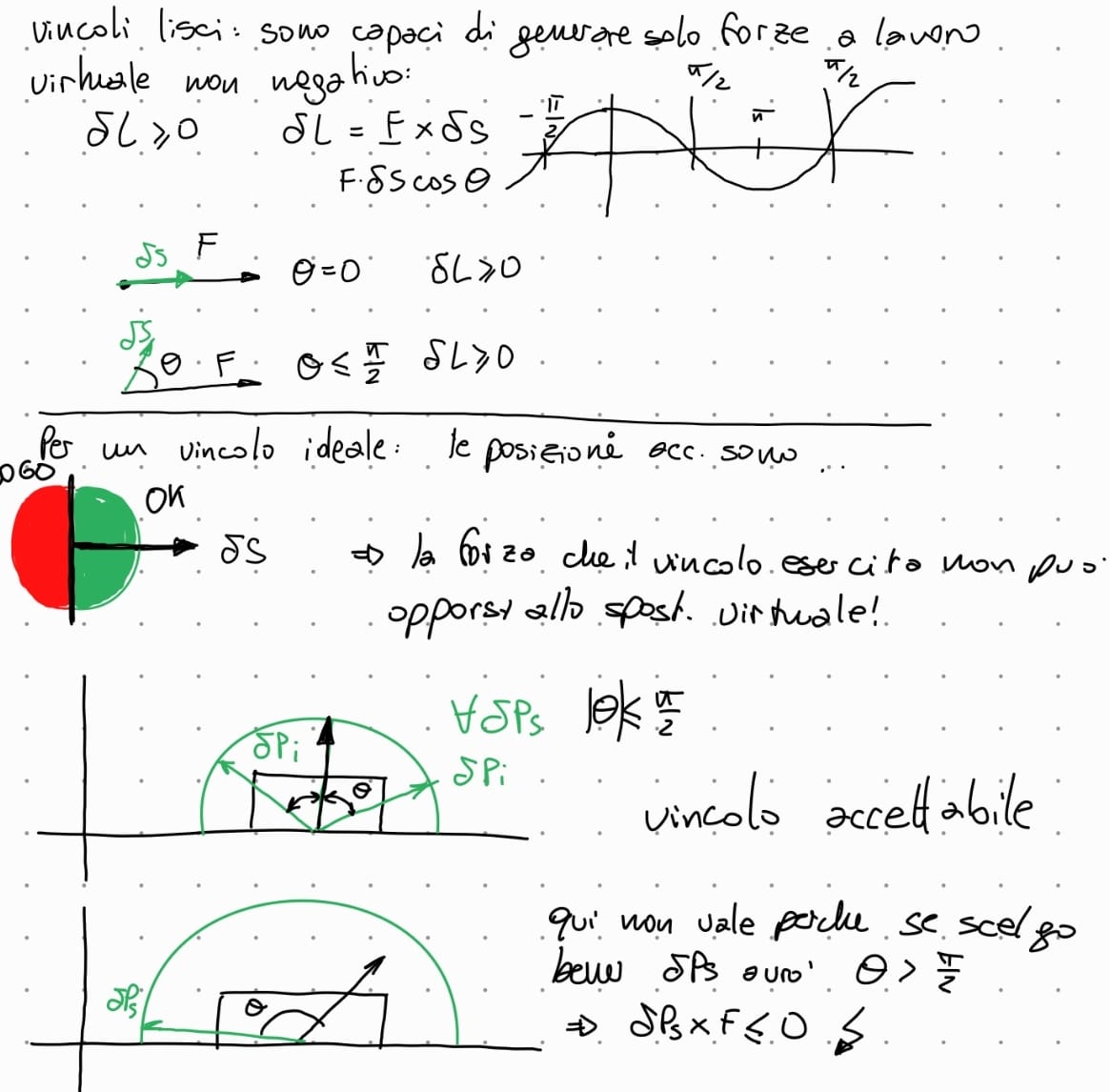
definizione di posizione di equilibrio, in parole

se metto un punto materiale P in una posizione di equilibrio e se all’istante iniziale t=0 ha velocità nulla, allora il punto P rimante nella posizione di equilibrio in modo permanente

equilibrio di una PARTICELLA (un punto materiale)
quale è la condizione sufficiente e necessaria affinche un punto materiale P sia in condizione di equilibrio:

la risultante agente su il punto P deve essere nulla:

R = 0 la risultante si compone della somma delle forze attive e quelle vincolari:
F + Φ = 0

equilibrio di un CORPO (sistema di punti materiali)

quale è la condizione affinchè un corpo sia in equilibrio

condizione sufficente e necessaria affinche un corpo sia in equilibrio è che:
la somma di tutte le forze su ogni punto materiale Ps è nulla!

quali sono i due metodi per trovare le posizioni di equilibrio di un corpo?

1. equazioni cardinali della stativa

   1. principio dei lavori virtuali

formulare le equazioni cardinali della statica per

1. corpo qualsiasi soggetto a sistema di forze

2. corpo rigido soggetto a sistema di forze

1. corpo QUALSIASI:
   la condizione necessaria (e non sufficiente) affinche un corpo qualsiasi sia in equilibrio è
   R^(e) = 0 —> R^{(e, a)} + R^{(e, v)} = 0
   M_o^(e) = 0 —> M_o^{(e, a)} + M_o^{(e, v)} = 0

2. corpo RIGIDO
   condizione necessaria e sufficiente per l’equilibrio
   

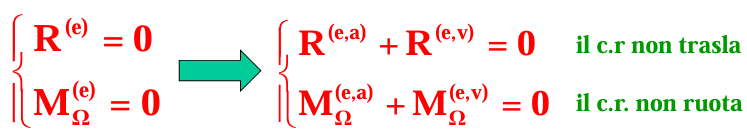
quale è la condizione affinchè un sistema di corpi rigidi sia in equilibrio ?

l’insieme del corpo rigido si puo scomporre in sotto sistemi, se ogni sottosistema è in equilibrio allora l’intero corpo rigido lo è

nella scomposizione di un sistema di corpi rigidi che conseguenza ha la legge di azione reazione sulle forze vincolari

se scompongo un corpo in due sottosistemi, allora le forze interne / forze vincolari si annullano la una con la altra e per la 3 legge di newton hanno verso opposto

come si puo trovare il baricentro di un corpo in modo sperimentale (x2 modi)

1. metodo della sospensione, si sospende un corpo per un punto, si lascia trovare posizione di equilibrio, poi si traccia linea vertivale dal punto di sospensione, poi si ripete con un altro punto e la intersezinoe delle rette è il BC

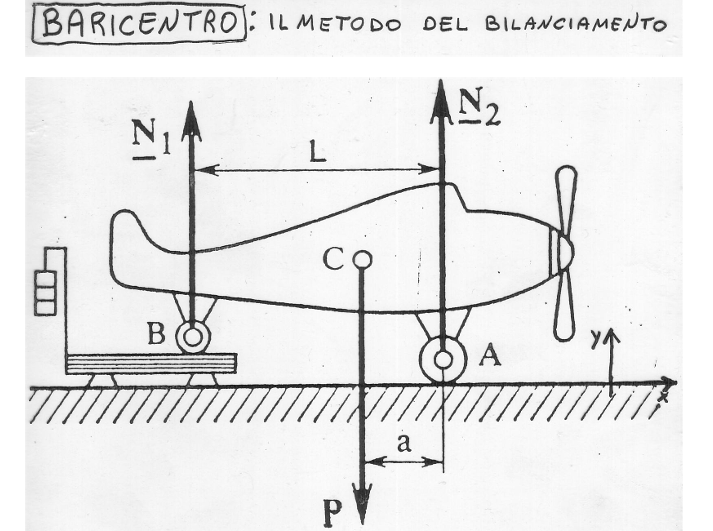
2. metodo del bilanciametno con una bilancia

enunciare il principio dei lavori virtuali,
che cosa cambia se i vincoli non sono ideali

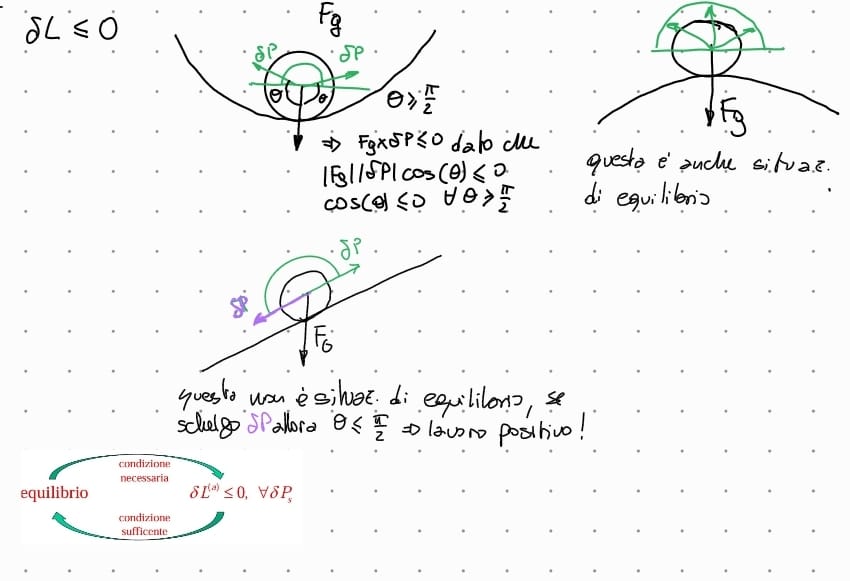
la condizione necessaria e sufficiente per un sistema meccanicp a vincoli ideali sia in una configurazione C di equilibrio è che: il lavoro virtuale delle forze attive sia non positivo per ogni spostamento virtuale da C
caso speciale, se gli spostamenti sono reversibili —> il lavoro è nullo

che cosa sono le configurazioni di equilibrio per un sistema olonomo

come devono essere i vincoli

come si trovano le posizioni di equilibrio per un sistema olonomo a due gradi di libertà,

anche qui come nel sistema olonomo ad un gradi di libertà bisogna trovare quando il potenziale si annulla! solo che il potenziale in questo caso è una funzione in due variabili

Dimostrazione / deduzione del

1. principio dei lavori virtuali

2. il caso speciale dove gli spostamenti sono reversibili

dedurre le equazioni caridnali della statica

Supponendo che inizialmente un sistema si in una configurazione di equilibrio. quali tre tipi di equilibrio ci sono

equilibrio stabile, instabile ed indifferente:

1. equilibrio Stabile, se perturbato di poco il sistema esso tende a tornare nella posizione di equilibrio

2. equilibrio instabile, se perturbo il sistema esso tende ad allontanarsi dalla posizione di equilibrio

3. equilibrio indifferente, se perturbo il sistema esso rimane per tutti i tempi nella nuova posizione

spiegare la differenza tra equilibrio stabile ed instabile dal punto di vista energetico

per un sistema in equilibrio stabile, applicando uno spostamento effettivo facendo (percio facendo attenzione ai vincoli), il lavoro delle forze attive è negativo,

invece per un sistema in equilibrio instabile, il lavoro delle forze attive è positivo per un spostamento effettivo

come cambia lo studio delle posizione di equilibrio per un sistema con forze conservative:

dato che le forze sono conservative —> esiste un potenziale e il lavoro da A a B si puo calcolare come la differenza di potenziale: L = U(B) - U(A)

in questo caso vale:

1. la configurazione P* è stabile se per un piccolo spostamento reale la variazione di potenziale ΔU < 0 <=> U(P) - U(P*) < 0 e perciò se U(P) < U(P*).
   →Se U ha un massimo in P*, allora la configurazione P* è di equilibrio stabile

2. qui invece c’è il problema della inversione del teorema di stabilità di D-L

che cosa dice il teorema di DIRICHLET - LAGRANGE

se un sistema olonomo a vincoli indipendenti dal tempo è conservativo ed il potenziale presenta un massimo relativo isolato in una configurazione di equlibrio ordinario C, allora C è una configurazione di equilibrio stabile

il teorema di DIRICHLET - LAGRANGE vale anche per forze non censervative?

Sì, dato che sono dissipative non aumentano la energia del sistema

quale è il problema di dell’inversione del problema di D-L

il teorema di DL ci dice che i massimi relativi isolati del potenziale dei sistemi olonomi conservativi sono stabili. ma non ci dice nulla sulla stabilità / instabilità dei minimi o dei punti di sella.

regola pratica per lo studio della stabilità dei sistemi con 1 grado di libertà:

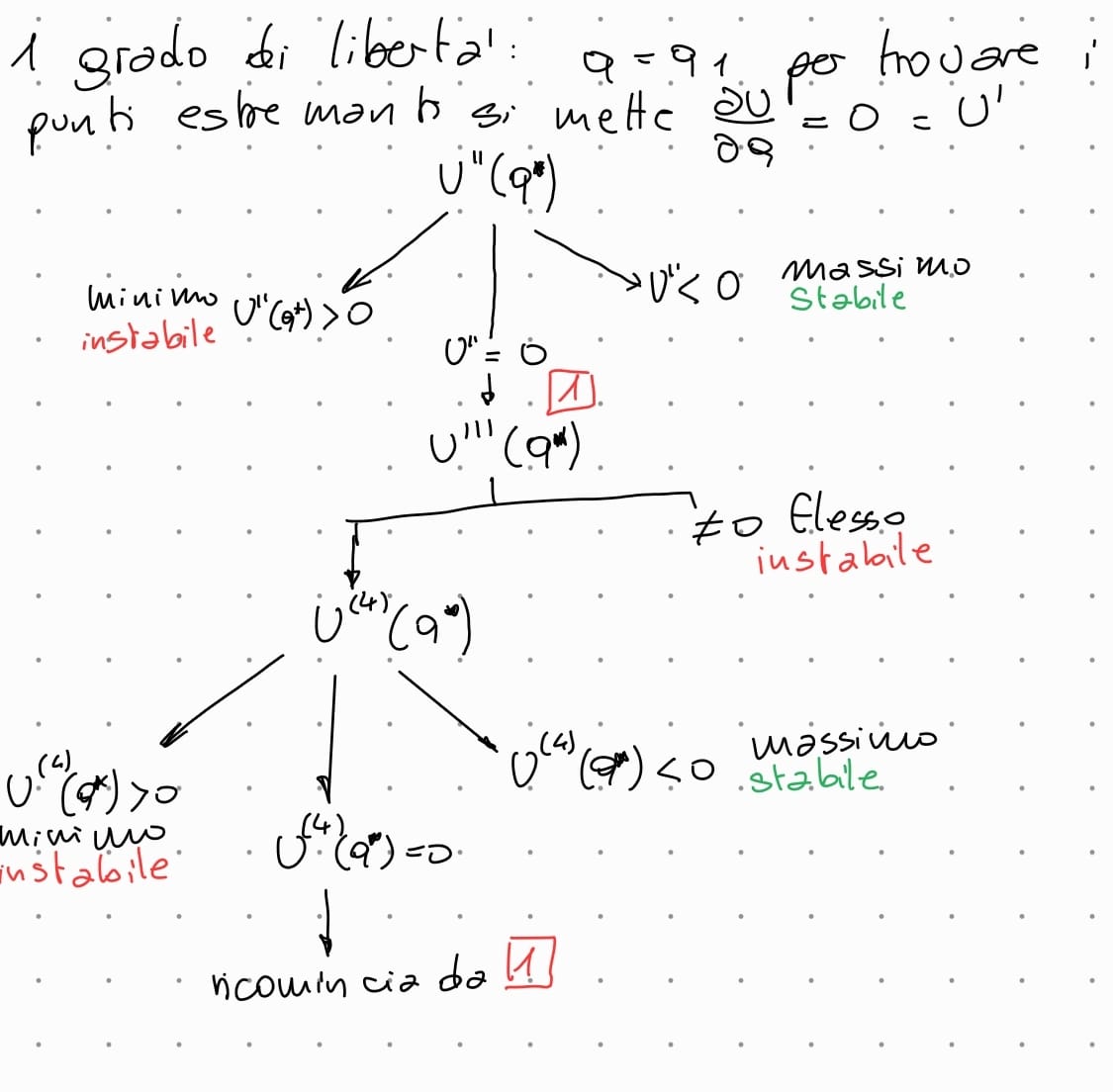
regola pratica per lo studio della stabilità dei sistemi con 2 grado di libertà: