data structures test 3 ch 10-13, 15

Draw a full binary tree with at least 6 nodes.

Draw a complete binary tree with exactly six nodes. Put a different value in each node. Then draw an array with six components and show where each of the six node values would be placed in the array (using the usual array representation of a complete binary tree).

Write the private member variables for a new node definition that could be used for a node in a tree where: (1) Each node contains int data, (2) Each node has up to four children, and (3) Each node also has a pointer to its parent. Store the pointers to the children in an array of four pointers.

private:

int data;

TreeNode* parent;

TreeNode* children[4];

Draw a binary taxonomy tree that can be used for these four animals: Rabbit, Horse, Whale, Snake.

template <class Item>

void subswap(binary_tree_node<Item>* root_ptr)

{

if (root_ptr == nullptr)

return;

binary_tree_node<Item>* temp = root_ptr->left();

root_ptr->set_left(root_ptr->right());

root_ptr->set_right(temp);

}

template <class Item>

void flip(binary_tree_node<Item>* root_ptr)

{

if (root_ptr == nullptr)

return;

binary_tree_node<Item>* temp = root_ptr->left();

root_ptr->set_left(root_ptr->right());

root_ptr->set_right(temp);

flip(root_ptr->left());

flip(root_ptr->right());

}

a. 1 2 3 14 7 10 40 30 11
b. 14 2 1 3 11 10 7 30 40
c. 1 3 2 7 10 40 30 11 14

template <class Item>

void increase(binary_tree_node<Item>* root_ptr)

{

if (root_ptr == nullptr)

return;

root_ptr->set_data(root_ptr->data() + 1);

increase(root_ptr->left());

increase(root_ptr->right());

}

Using the binary_tree_node from Section 10.3, write a recursive function to meet the following specification. You do not need to check the precondition.

template <class Item>
size_t many_nodes(binary_tree_node<Item>* root_ptr)
// Precondition: root_ptr is the root pointer of a binary tree.
// Postcondition: The return value is the number of nodes in the tree.
// NOTES: The empty tree has 0 nodes, and a tree with just a root has
// 1 node.

template <class Item>

size_t many_nodes(binary_tree_node<Item>* root_ptr)

{

if (root_ptr == nullptr)

return 0;

return 1 + many_nodes(root_ptr->left()) + many_nodes(root_ptr->right());

}

Using the binary_tree_node from Section 10.3, write a recursive function to meet the following specification. You do not need to check the precondition.

template <class Item>
int tree_depth(binary_tree_node<Item>* root_ptr)
// Precondition: root_ptr is the root pointer of a binary tree.
// Postcondition: The return value is the depth of the binary tree.
// NOTES: The empty tree has a depth of -1 and a tree with just a root
// has a depth of 0.

template <class Item>

int tree_depth(binary_tree_node<Item>* root_ptr)

{

if (root_ptr == nullptr)

return -1;

int left_depth = tree_depth(root_ptr->left());

int right_depth = tree_depth(root_ptr->right());

return 1 + std::max(left_depth, right_depth);

}

Using the binary_tree_node from Section 10.3, write a function to meet the following specification. You do not need to check the precondition.

template <class Item>
size_t count42(binary_tree_node<Item>* root_ptr)
// Precondition: root_ptr is the root pointer of a binary tree (but
// NOT NECESSARILY a search tree).
// Postcondition: The return value indicates how many times 42 appears
// in the tree. NOTE: If the tree is empty, the function returns zero.

template <class Item>

size_t count42(binary_tree_node<Item>* root_ptr)

{

if (root_ptr == nullptr)

return 0;

size_t count = (root_ptr->data() == 42) ? 1 : 0;

return count + count42(root_ptr->left()) + count42(root_ptr->right());

}

Using the binary_tree_node from Section 10.3, write a function to meet the following specification. You do not need to check the precondition.

template <class Item>
bool has_42(binary_tree_node<Item>* root_ptr)
// Precondition: root_ptr is the root pointer of a binary tree (but
// NOT NECESSARILY a search tree).
// Postcondition: The return value indicates whether 42 appears somewhere
// in the tree. NOTE: If the tree is empty, the function returns false.

template <class Item>

bool has_42(binary_tree_node<Item>* root_ptr)

{

if (root_ptr == nullptr)

return false;

if (root_ptr->data() == 42)

return true;

return has_42(root_ptr->left()) || has_42(root_ptr->right());

}

Using the binary_tree_node from Section 10.3, write a function to meet the following specification. You do not need to check the precondition.

template <class Item>

bool all_42(binary_tree_node<Item>* root_ptr)

// Precondition: root_ptr is the root pointer of a binary tree (but

// NOT NECESSARILY a search tree).

// Postcondition: The return value is true if every node in the tree

// contains 42. NOTE: If the tree is empty, the function returns true.

template <class Item>

bool all_42(binary_tree_node<Item>* root_ptr)

{

if (root_ptr == nullptr)

return true;

if (root_ptr->data() != 42)

return false;

return all_42(root_ptr->left()) && all_42(root_ptr->right());

}

Using the binary_tree_node from Section 10.3, write a recursive function to meet the following specification. You do not need to check the precondition.

template <class Item>

int sum_all(binary_tree_node<Item>* root_ptr)

// Precondition: root_ptr is the root pointer of a binary tree.

// Postcondition: The return value is the sum of all the data in all the nodes.

// NOTES: The return value for the empty tree is zero.

template <class Item>

int sum_all(binary_tree_node<Item>* root_ptr)

{

if (root_ptr == nullptr)

return 0;

return root_ptr->data() + sum_all(root_ptr->left()) + sum_all(root_ptr->right());

}

Suppose that we want to create a binary search tree where each node contains information of some data type called Item (which has a default constructor and a correct value semantics). What additional factor is required for the Item data type?

must support a comparison using the less than operator. without it, the tree can’t determine correct placement of elements.

Suppose that a binary search tree contains the number 42 at a node with two children. Write two or three clear sentences to describe the process required to delete the 42 from the tree.

Find the largest value in the predecessor or the smallest in the successor. replace 42 with either the predecessor or successor and then recursively delete predecessor or successor node

Using the binary_tree_node from Section 10.3, write a function to meet the following specification. You do not need to check the precondition. Make the function as efficient as possible (do not visit nodes unnecessarily):

template <class Item>

size_t count42(binary_tree_node<Item>* root_ptr)

// Precondition: root_ptr is the root pointer of a binary SEARCH tree.

// Postcondition: The return value indicates how many times 42 appears

// in the tree.

template <class Item>

size_t count42(binary_tree_node<Item>* root_ptr)

{

if (root_ptr == nullptr)

return 0;

if (root_ptr->data() == 42)

return 1 + count42(root_ptr->left()) + count42(root_ptr->right());

else if (root_ptr->data() > 42)

return count42(root_ptr->left());

else // root_ptr->data() < 42

return count42(root_ptr->right());

}

Using the binary_tree_node from Section 10.3, write a function to meet the following specification. You do not need to check the precondition. Make the function as efficient as possible (do not visit nodes unnecessarily):

template <class Item>

int max(binary_tree_node<Item>* root_ptr)

// Precondition: root_ptr is the root pointer of a nonempty binary SEARCH

// tree.

// Postcondition: The return value is the largest value in the tree.

template <class Item>

int max(binary_tree_node<Item>* root_ptr)

{

while (root_ptr->right() != nullptr)

root_ptr = root_ptr->right();

return root_ptr->data();

}

Using the binary_tree_node from Section 10.3, write a function to meet the following specification. You do not need to check the precondition.

template <class Item>

void insert_one_42(binary_tree_node<Item>*& root_ptr)

// Precondition: root_ptr is the root pointer of a binary SEARCH tree.

// Postcondition: One copy of the number 42 has been added to the binary

// search tree.

template <class Item>

void insert_one_42(binary_tree_node<Item>*& root_ptr)

{

if (root_ptr == nullptr)

{

root_ptr = new binary_tree_node<Item>(42);

return;

}

if (42 < root_ptr->data())

insert_one_42(root_ptr->left());

else

insert_one_42(root_ptr->right());

}

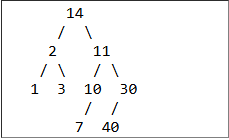
There is a tree in the box at the top of this section. How many leaves does it have?

• A. 2

• B. 4

• C. 6

• D. 8

• E. 9

• B. 4

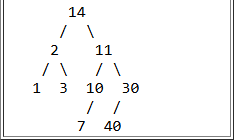
There is a tree in the box at the top of this section. How many of the nodes have at least one sibling?

A. 5

B. 6

C. 7

D. 8

E. 9

D. 8

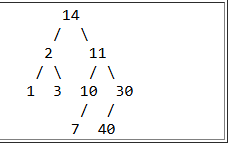
There is a tree in the box at the top of this section. What is the value stored in the parent node of the node containing 30?

A. 10

B. 11

C. 14

D. 40

E. None of the above

B. 11

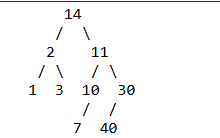
There is a tree in the box at the top of this section. How many descendants does the root have?

A. 0

B. 2

C. 4

D. 8

D. 8

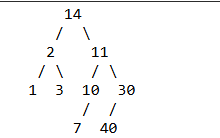
There is a tree in the box at the top of this section. What is the depth of the tree?

A. 2

B. 3

C. 4

D. 8

E. 9

B. 3

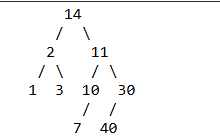
There is a tree in the box at the top of this section. How many children does the root have?

A. 2

B. 4

C. 6

D. 8

E. 9

A. 2

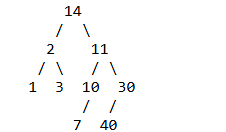
Consider the binary tree in the box at the top of this section. Which statement is correct?

A. The tree is neither complete nor full.

B. The tree is complete but not full.

C. The tree is full but not complete.

D. The tree is both full and complete.

A. The tree is neither complete nor full.

What is the minimum number of nodes in a full binary tree with depth 3?

A. 3

B. 4

C. 8

D. 11

E. 15

E. 15

What is the minimum number of nodes in a complete binary tree with depth 3?

A. 3

B. 4

C. 8

D. 11

E. 15

C. 8

Select the one true statement.

A. Every binary tree is either complete or full.

B. Every complete binary tree is also a full binary tree.

C. Every full binary tree is also a complete binary tree.

D. No binary tree is both complete and full.

C. Every full binary tree is also a complete binary tree.

Suppose T is a binary tree with 14 nodes. What is the minimum possible depth of T?

A. 0

B. 3

C. 4

D. 5

B. 3

Select the one FALSE statement about binary trees:

A. Every binary tree has at least one node.

B. Every non-empty tree has exactly one root node.

C. Every node has at most two children.

D. Every non-root node has exactly one parent.

A. Every binary tree has at least one node.

Consider the binary_tree_node from Section 10.3. Which expression indicates that t represents an empty tree?

A. (t == NULL)

B. (t->data( ) == 0)

C. (t->data( ) == NULL)

D. ((t->left( ) == NULL) && (t->right( ) == NULL))

A. (t == NULL)

Consider the node of a complete binary tree whose value is stored in data[i] for an array implementation. If this node has a right child, where will the right child's value be stored?

A. data[i+1]

B. data[i+2]

C. data[2*i + 1]

D. data[2*i + 2]

D. data[2*i + 2]

How many recursive calls usually occur in the implementation of the tree_clear function for a binary tree?

A. 0

B. 1

C. 2

C. 2

Suppose that a binary taxonomy tree includes 8 animals. What is the minimum number of NONLEAF nodes in the tree?

A. 1

B. 3

C. 5

D. 7

E. 8

D. 7

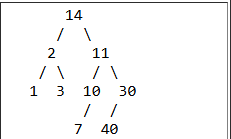
There is a tree in the box at the top of this section. What is the order of nodes visited using a pre-order traversal?

A. 1 2 3 7 10 11 14 30 40

B. 1 2 3 14 7 10 11 40 30

C. 1 3 2 7 10 40 30 11 14

D. 14 2 1 3 11 10 7 30 40

D. 14 2 1 3 11 10 7 30 40

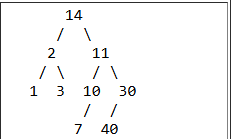
There is a tree in the box at the top of this section. What is the order of nodes visited using an in-order traversal?

A. 1 2 3 7 10 11 14 30 40

B. 1 2 3 14 7 10 11 40 30

C. 1 3 2 7 10 40 30 11 14

D. 14 2 1 3 11 10 7 30 40

B. 1 2 3 14 7 10 11 40 30

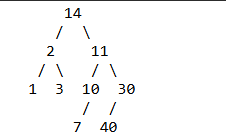
There is a tree in the box at the top of this section. What is the order of nodes visited using a post-order traversal?

A. 1 2 3 7 10 11 14 30 40

B. 1 2 3 14 7 10 11 40 30

C. 1 3 2 7 10 40 30 11 14

D. 14 2 1 3 11 10 7 30 40

C. 1 3 2 7 10 40 30 11 14

D- 5

Suppose that we want to create a heap where each node contains information of some data type called Item (which has a default constructor and a correct value semantics). What additional factor is required for the Item data type?

A comparison operator is required usually the less than operator.

A heap is a binary tree where the entries can be compared using the usual six comparison operations (that form a total order semantics). Write the two rules that the binary tree must follow in order for the structure to actually be a heap.

1. Heap order property

2. Complete binary tree property

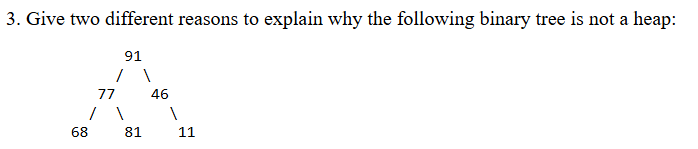
• The parent node 71 is less than its child 81, violating the heap order property.

• The tree is not complete because node 46 has a right child but no left child.

910

/ \

82 66

/ \ / \

77 1 3 11

/

68

77

/ \

68 66

/ \ /

11 1 3

Suppose that you are performing a reheapification downward. Write a precise condition that describes the situation that causes the reheapification to stop.

in a max-heap: The current node is greater than or equal to both of its children, or it has no children.

Suppose that you are performing a reheapification upward. Write a precise condition that describes the situation that causes the reheapification to stop.

in a max heap: The current node is less than or equal to its parent, or the current node becomes the root.

Suppose that a non-leaf node in a B-tree contains 42 entries. How many children does the node have?

43 children

Draw an example of a B-tree with four nodes and seven integer entries. The value of MINIMUM is 1 for this tree.

[4]

/ \

[2] [6]

/ \ / \

[1] [3] [5] [7]

[56]

/ \

[7] [66, 82]

/ \ / | \

[2] [8] [63] [71] [93]

[56]

/ \

[7] [71]

/ \ / \

[2] [8] [66][93]

Suppose that a B-tree is declared so that MAXIMUM (the maximum number of items in a node) is 84. What is the value of MINIMUM (the minimum number of items in a non-root node)?

42

Suppose that a B-tree is declared so that MAXIMUM (the maximum number of items in a node) is 84. Write one clear sentence to describe why each node's data array is set up to hold up to 85 items (one more than MAXIMUM).

to account for extra item during insertion before the node splits

Suppose that a and b are two positive integers and n is some non-negative number. Write an equation to show the relationship between log base a of n and log base b of n. Give a derivation to show that the relationship is valid.

What feature of heaps allows them to be efficiently implemented using a partially filled array?

A. Heaps are binary search trees.

B. Heaps are complete binary trees.

C. Heaps are full binary trees.

D. Heaps contain only integer data.

B. Heaps are complete binary trees.

If a heap is implemented using a partially filled array called data, and the array contains n elements (n > 0), where is the entry with the greatest value?

A. data[0]

B. data[n-1]

C. data[n]

D. data[2*n + 1]

E. data[2*n + 2]

A. data[0]

Select the true statement about the worst-case time for operations on heaps.

A. Niether insertion nor removal is better than linear.

B. Insertion is better than linear, but removal is not.

C. Removal is better than linear, but insertion is not.

D. Both insertion and removal are better than linear.

D. Both insertion and removal are better than linear.

Suppose that we have implemented a priority queue by storing the items in a heap (using an array for the heap items). We are now executing a reheapification upward and the out-of-place node is at data[i] with priority given by data[i]. Which of the following boolean expressions is TRUE to indicate that the reheapification IS NOT YET DONE.

A. (i > 0)

B. (data[(i-1)/2] < data[i])

C. (i > 0) && (data[(i-1)/2] < data[i])

D. (i > 0) || (data[(i-1)/2] < data[i])

C. (i > 0) && (data[(i-1)/2] < data[i])

Suppose that we have implemented a priority queue by storing the items in a heap. We are now executing a reheapification downward and the out-of-place node has priority of 42. The node's parent has a priority of 72, the left child has priority 52 and the node's right child has priority 62. Which statement best describes the status of the reheapification.

A. The reheapification is done.

B. The next step will interchange the two children of the out-of-place node.

C. The next step will swap the out-of-place node with its parent.

D. The next step will swap the out-of-place node with its left child.

E. The next step will swap the out-of-place node with its right child.

E. The next step will swap the out-of-place node with its right child.

Which formula is the best approximation for the depth of a heap with n nodes?

A. log (base 2) of n

B> The number of digits in n (base 10)

C. The square root of n

D. n

E. The square of n

A. log (base 2) of n

Which statement is true for a B-tree?

A. All entries of a node are greater than or equal to the entries in the node's children.

B. All leaves are at the exact same depth.

C. All nodes contain the exact same number of entres.

D. All non-leaf nodes have the exact same number of children.

B. All leaves are at the exact same depth.

Suppose that a non-leaf node in a B-tree has 41 entries. How many children will this node have?

A. 2

B. 40

C. 41

D. 42

e. 82

D. 42

Suppose that a B-tree has MAXIMUM of 10 and that a node already contains the integers 1 through 10. If a new value, 11, is added to this node, the node will split into two pieces. What values will be in these two pieces?

A. The first piece will have only 1 and the second piece will have the rest of the numbers.

B. The first piece will have 1 through 5 and the second piece will have 6 through 11.

C. The first piece will have 1 through 5 and the second piece will have 7 through 11.

D. The first piece will have 1 through 6 and the second piece will have 7 through 11.

E. The first piece will have 1 through 10 and the second piece will have only 11.

C. The first piece will have 1 through 5 and the second piece will have 7 through 11.

Suppose that X is a B-tree leaf containing 41 entries and having at least one sibling. Which statement is true?

A. Any sibling of X is also a leaf.

B. Any sibling of X contains at least 41 entries.

C. The parent of X has exactly 42 entries.

D. X has at least 41 siblings.

A. Any sibling of X is also a leaf.

Suppose you run a O(log n) algorithm with an input size of 1000 and the algorithm requires 110 operations. When you double the input size to 2000, the algorithm now requires 120 operations. What is your best guess for the number of operations required when you again double the input size to 4000?

A. 130

B. 140

C. 150

D. 160

E. 170

A. 130

Tree algorithms typically run in time O(d) . What is d?

A. The depth of the tree.

B. The number of divisions at each level.

C. The number of entries in each node.

D. The number of nodes in the tree.

E. The total number of entries in all the nodes of the tree.

A. The depth of the tree.

Here is an array with exactly 15 elements:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Suppose that we are doing a serial search for an element. Circle any elements that will be found by examining two or fewer numbers from the array.

1 and 2

Here is an array with exactly 15 elements:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Suppose that we are doing a binary search for an element. Circle any elements that will be found by examining two or fewer numbers from the array.

4, 8, and 12

Implement the body of the following function using a binary search of the array. You do not need to check the precondition. All your local variables must be size_t variables.

bool has_42(const int data[ ], size_t n)

// Precondition: The elements data[0]...data[n-1] are sorted from smallest

// to largest. The value of n might be zero (indicating an empty

// array).

// Postcondition: A true return value indicates that the number 42 appears in

// data[0]...data[n-1]. A false return value indicates that 42 doesn�t appear.

bool has_42(const int data[], size_t n)

{

size_t left = 0;

size_t right = (n == 0) ? 0 : n - 1;

while (left <= right)

{

size_t mid = left + (right - left) / 2;

if (data[mid] == 42)

return true;

else if (data[mid] < 42)

left = mid + 1;

else

right = (mid == 0) ? 0 : mid - 1;

}

return false;

}

Draw a hash table with open addressing and a size of 9. Use the hash function "k%9". Insert the keys: 5, 29, 20, 0, 27 and 18 into your table (in that order).

Index	Value
0	0
1	27
2	29
3	20
4	18
5	5
6	—
7	—
8	—

Suppose you are building an open address hash table with double hashing. The hash table capacity is n, so that the valid hash table indexes range from 0 to n. Fill in the blanks:

In order to ensure that every array position is examined, the value returned by the second hash function must be ________________________ with respect to n.

One way to ensure this good behavior is to make n be _______________, and have the return value of the second hash function range from _________ to _________ (including the end points).

relatively prime, prime number, 1, n-1

You are writing code for the remove member function of a chained hash table. Fill in the blanks in this pseudocode with the two missing statements. You may use pseudocode yourself, or write actual C++ code:

void Table::remove(int key)

{

Node cursor;

size_t i;

1. i = hash(key);

2. Make cursor point to the node that contains an item with the given key

(or set it to NULL if there is no such node).

3. if (cursor != NULL)

{

3a. _____________________________________________________________

3b. _____________________________________________________________

}

// 3a. Remove the node from the list

if (prev == nullptr)

table[i] = cursor->link; // Node is at head

else

prev->link = cursor->link; // Node is in middle or end

// 3b. Free the memory of the removed node

delete cursor;

Draw a hash table with chaining and a size of 9. Use the hash function "k%9" to insert the keys 5, 29, 20, 0, and 18 into your table.

Index	Chain
0	18 → 0
1	—
2	20 → 29
3	—
4	—
5	5
6	—
7	—
8	—

Suppose that I have the following record_type definition for a record in a hash table:

    struct record_type
    {
        int key;
        ... other stuff may also appear here ...
    };

The hash table uses open addressing with linear probing. The table size is a global constant called CAPACITY. Locations of the table that have NEVER been used will contain the key -1. Locations of the table that were once used but are now vacant will contain the key -2. All valid keys will be non-negative, and the hash function is:

    size_t hash(int key)
    {
        return (key % CAPACITY);
    }

Complete the implementation of the following function. There is no need to check the precondition, but your code must be as efficient as possible.

bool key_occurs(const record_type data[ ], int search_key)
// Precondition: data[0]...data[CAPACITY-1] is an open address hash table
// as described above.
// Postcondition: If search_key occurs as a key of a record in the table, then
// the function returns true; otherwise the function returns false.

bool key_occurs(const record_type data[], int search_key)

{

size_t i = hash(search_key);

size_t count = 0;

while (count < CAPACITY && data[i].key != -1) // stop if full loop or never-used slot

{

if (data[i].key == search_key)

return true;

i = (i + 1) % CAPACITY; // linear probing

++count;

}

return false;

}

Suppose that an open-address hash table has a capacity of 811 and it contains 81 elements. What is the table's load factor? (An appoximation is fine.)

Approximately 0.1 (or 10%)

I plan to put 1000 items in a hash table, and I want the average number of accesses in a successful search to be about 2.0.

A. About how big should the array be if I use open addressing with linear probing? NOTE: For a load factor of A, the average number of accesses is generally ½(1+1/(1-A)).

B. About how big should the array be if I use chained hashing? NOTE: For a load factor of A, the average number of accesses is generally (1+A/2).

A. 1500
b. 500

What is the worst-case time for serial search finding a single item in an array?

A. Constant time

B. Logarithmic time

C. Linear time

D. Quadratic time

C. Linear time

What is the worst-case time for binary search finding a single item in an array?

A. Constant time

B. Logarithmic time

C. Linear time

D. Quadratic time

B. Logarithmic time

What additional requirement is placed on an array, so that binary search may be used to locate an entry?

A. The array elements must form a heap.

B. The array must have at least 2 entries.

C. The array must be sorted.

D. The array's size must be a power of two.

C. The array must be sorted.

What is the best definition of a collision in a hash table?

A. Two entries are identical except for their keys.

B. Two entries with different data have the exact same key.

C. Two entries with different keys have the same exact hash value.

D. Two entries with the exact same key have different hash values.

C. Two entries with different keys have the same exact hash value.

Which guideline is NOT suggested from from empirical or theoretical studies of hash tables:

A. Hash table size should be the product of two primes.

B. Hash table size should be the upper of a pair of twin primes.

C. Hash table size should have the form 4K+3 for some K.

D. Hash table size should not be too near a power of two.

B. Hash table size should be the upper of a pair of twin primes.

In an open-address hash table there is a difference between those spots which have never been used and those spots which have previously been used but no longer contain an item. Which function has a better implementation because of this difference?

A. insert

B. is_present

C. remove

D. size

E. Two or more of the above functions

E. Two or more of the above functions

What kind of initialization needs to be done for an open-address hash table?

A. None.

B. The key at each array location must be initialized.

C. The head pointer of each chain must be set to NULL.

D. Both B and C must be carried out.

B. The key at each array location must be initialized.

What kind of initialization needs to be done for an chained hash table?

A. None.

B. The key at each array location must be initialized.

C. The head pointer of each chain must be set to NULL.

D. Both B and C must be carried out.

C. The head pointer of each chain must be set to NULL.

A chained hash table has an array size of 512. What is the maximum number of entries that can be placed in the table?

A. 256

B. 511

C. 512

D. 1024

E. There is no maximum.

E. There is no maximum.

Suppose you place m items in a hash table with an array size of s. What is the correct formula for the load factor?

A. s + m

B. s - m

C. m - s

D. m * s

E. m / s

E. m / s

Here is an array of ten integers:

5 3 8 9 1 7 0 2 6 4

Draw this array after the FIRST iteration of the large loop in a selection sort (sorting from smallest to largest

0 3 8 9 1 7 5 2 6 4

Here is an array of ten integers:

5 3 8 9 1 7 0 2 6 4

Draw this array after the FIRST iteration of the large loop in an insertion sort (sorting from smallest to largest). This iteration has shifted at least one item in the array!

0 3 8 9 1 7 8 2 6 4

Suppose that you are writing a program that has the usual selectionsort function available:

void selectionsort(int data[ ], size_t n);

Your program also has an integer array called x, with 10 elements. Write two function calls: The first call uses selectionsort to sort all of x; the second call uses selectionsort to sort x[3]..x[9].

selectionsort(x, 10);

selectionsort(x + 3, 7);

Describe a case where quicksort will result in quadratic behavior.

When pivot always picks the smallest or largest element(ex: sorting reverse sorted array)

Here is an array which has just been partitioned by the first step of quicksort:

3, 0, 2, 4, 5, 8, 7, 6, 9

Which of these elements could be the pivot? (There may be more than one possibility!)

4, 5

Give a concise accurate description of a good way for quicksort to choose a pivot element. Your approach should be better than "use the entry at location [0]".

A good way to choose a pivot is to use the median-of-three method: pick the median of the first, middle, and last elements and use the median of these 3 as a pivot

Give a concise accurate description of a good way for quicksort to improve its performance by using insertion sort.

Quicksort can switch to insertion sort when the subarray size falls below a certain threshold, The size of the subarray being sorted should be small.

Here is an array of ten integers:

5 3 8 9 1 7 0 2 6 4

Suppose we partition this array using quicksort's partition function and using 5 for the pivot. Draw the resulting array after the partition finishes.

3 1 0 2 4 5 8 9 7 6

Here is an array of ten integers:

5 3 8 9 1 7 0 2 6 4

Draw this array after the TWO recursive calls of merge sort are completed, and before the final merge step has occured.

1 3 5 8 9 0 2 4 6 7

Implement the following function:

void merge(int data[ ], size_t n1, size_t n2);

// Precondition: The first n1 elements of data are sorted, and the

// next n2 elements of data are sorted (from smallest to largest).

// Postcondition: The n1+n2 elements of data are now completely

// sorted.

void merge(int data[], size_t n1, size_t n2)

{

int i = 0, j = n1, k = 0;

int* temp = new int[n1 + n2];

while (i < n1 && j < n1 + n2) {

if (data[i] <= data[j]) temp[k++] = data[i++];

else temp[k++] = data[j++];

}

while (i < n1) temp[k++] = data[i++];

while (j < n1 + n2) temp[k++] = data[j++];

for (i = 0; i < n1 + n2; ++i) data[i] = temp[i];

delete[] temp;

}

Write two or three clear sentences to describe how a heapsort works.

Heapsort builds a max-heap from the array so the largest element is at the root. It then swaps the root with the last item, reduces the heap size, and heapifies again. This repeats until the array is sorted.

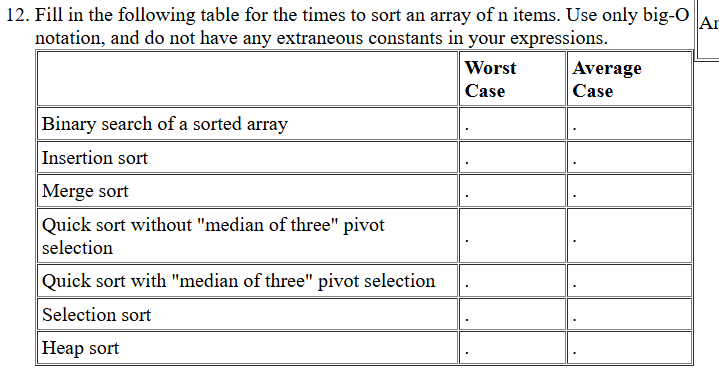
Algorithm	Worst Case	Average Case
Binary search of a sorted array	O(log n)	O(log n)
Insertion sort	O(n²)	O(n²)
Merge sort	O(n log n)	O(n log n)
Quick sort without "median of three" pivot selection	O(n²)	O(n log n)
Quick sort with "median of three" pivot selection	O(n²)	O(n log n)
Selection sort	O(n²)	O(n²)
Heap sort	O(n log n)	O(n log n)

Suppose that you are writing a program that has these two functions available:

int compare_ints(const void* p1, const void* p2);

// Precondition: p1 and p2 are really pointers to integers.

// Postcondition: The return value is:

// (a) negative if *p1 < *p2

// (b) zero if *p1 == *p2

// (c) positive if *p1 > *p2

void qsort(

void* base,

size_t n,

size_t bytes,

int compar(const void*, const void*)

);

// Same specification as the standard library qsort function.

Your program also has an integer array called x, with 10 elements. Write two function calls: The first call uses qsort to sort all of x; the second call uses qsort to sort x[3]..x[9].

First call (sorting all of x):
qsort(x, 10, sizeof(int), compare_ints);

Second call (sorting x[3]..x[9]):
qsort(x + 3, 7, sizeof(int), compare_ints);

Suppose that you implement quicksort nonrecursively using a stack, as in your last programming assignment. You use your algorithm to sort an array of 100 items, and at the start of the final iteration of the while loop, the stack contains just two numbers: 10 (on top) and 90 (on bottom). Write one or two clear sentences to describe which parts of the array are sorted at this point, and which parts of the array remain to be sorted.

At this point in the quicksort algorithm, the array is partitioned so that the first 10 elements are sorted and 90 remain to be sorted. The stack contains indices 10 and 90, indicating that the subarrays between indices 10 and 90 have not been sorted yet and the partitioning will continue in this range.