Math topics (Unit 1 - 3)

All from the assignment test on google classroom

When does a zero become a non-significant figure?

1. When it is at the end of the sequence with no decimal points (behind a number)

2. When it is in front and after a decimal (with no number accompanying them)

How to round up a number (4257.16) into 1,2,3,4,5 significant figures?

1. For one significant figure, 4000 (No need to put a decimal since it’ll make all the zeros significant)

2. For two significant figures, 4300 (We rounded up 2 because there was a 5 behind it)

3. For three significant figures, 4260

4. For four significant figures, 4257 (We didn’t need to round up our 7 because next to it is a 1)

5. For five significant figures, 4257.2 (We rounded up our 1 because next to it is a 6 and we put the decimal right where the original number has it)

Turn (158.1054) into 1,2,3,4 significant figures

1. For one significant figure, 200 (We round up our 1 because 5 was next to it)

2. For two significant figures, 160

3. For three significant figures, 158

4. For four significant figures, 158.1

5. For five significant figures, 158.11

Do you keep leading zeros even when they are not significant?

Yes, example, 0.0947268 turned into 3 significant figures is 0.0947

Perpendicular distance formula

1. (x,y) points, line is ax + by + c = 0

2. Perpendicular distance formula

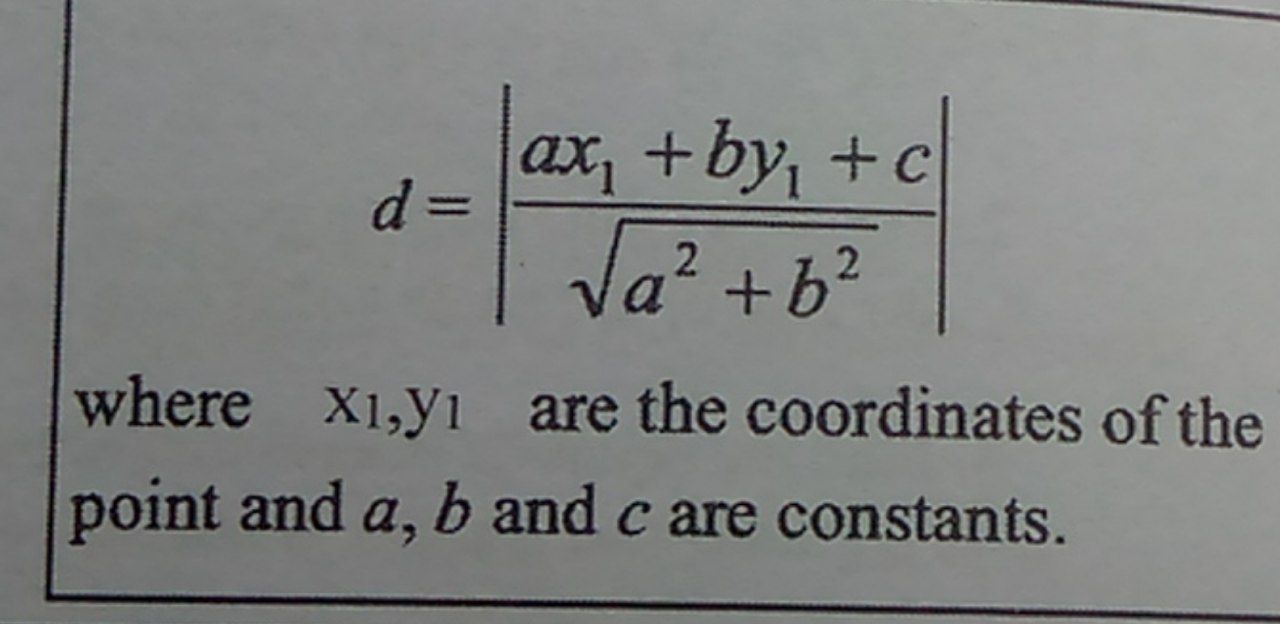
Formula for gradient (m) (Where is it used)

To find the gradient of the line with two given points

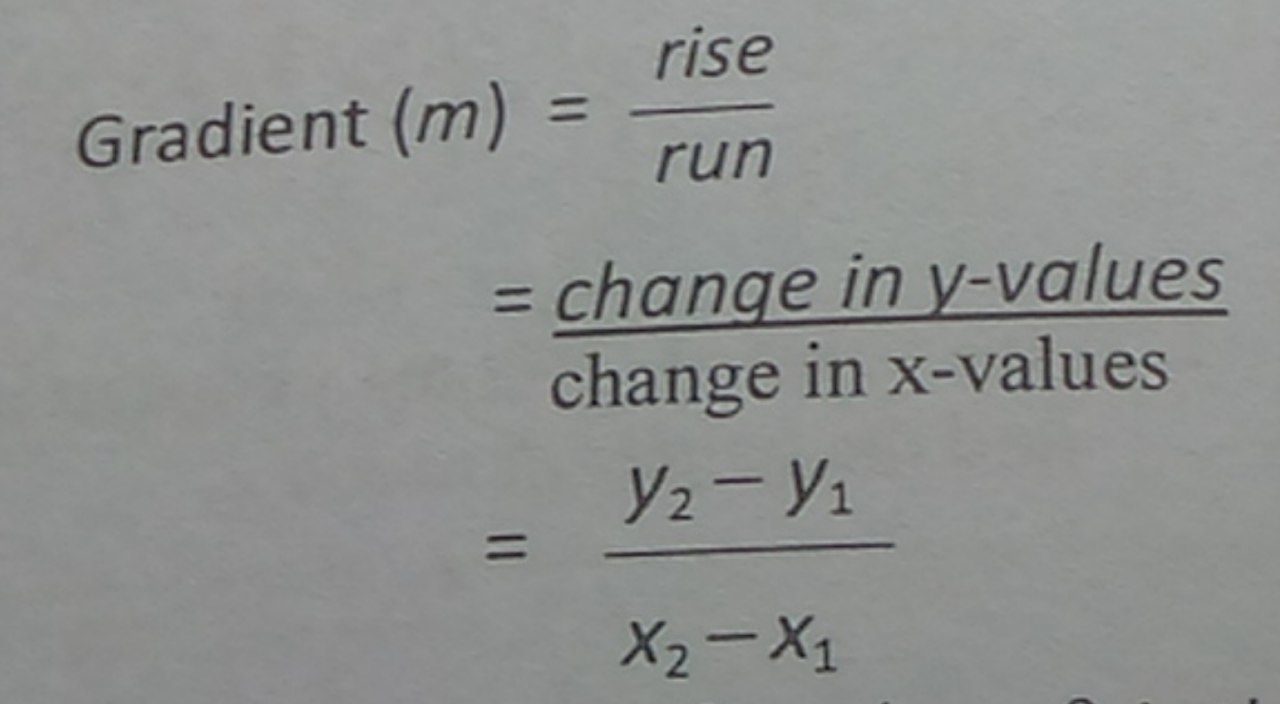
Point-gradient formula (where is it used)

It’s used to get the Ax + By + C = 0 format with only one given point

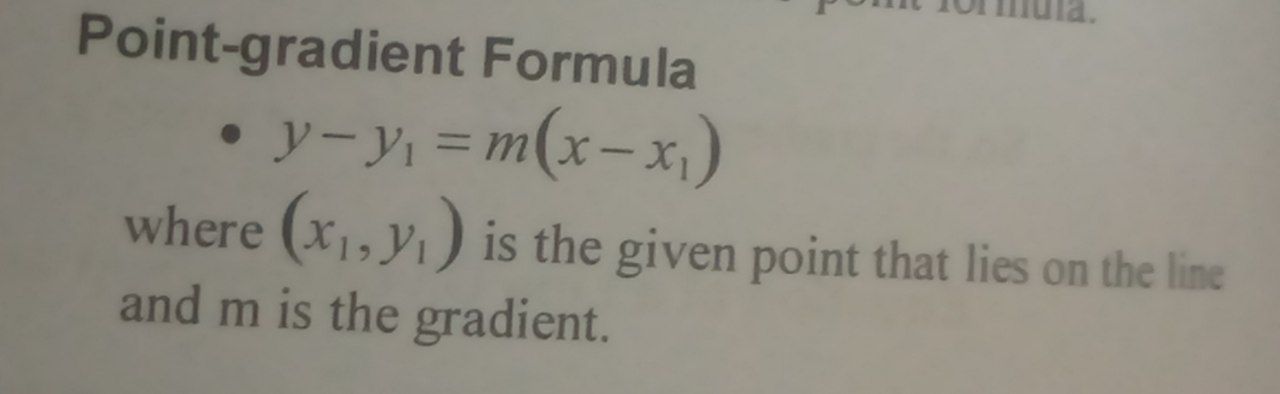
Format of finding perpendicular distance problems

1. Identifying (x , y), commonly it is given with “the point (x , y)”

2. Getting the gradient (m) by using the formula m = rise by run ) (y2 - y1 by x2 - x1)

3. After getting the m, use the point gradient formula to get the ax + by = c format so we can use the perpendicular formula

4. Use the perpendicular formula with the point (x,y)

5. Rationalize the answer if needed and don’t forget the mod, so it’s a positive answer

Circle formula to sketch a graph and find the radius

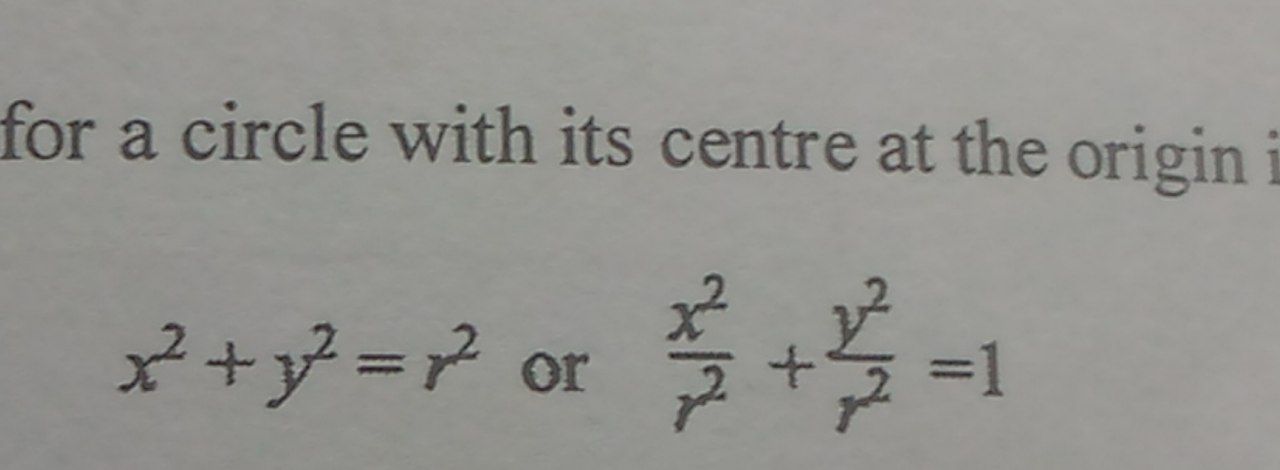
Format to sketch circles

1. recognize the x² + y² = r² formation

2. Find the radius

3. Identify if its a lower semi circle (y value is lower than zero meaning a minus is present) or circles

4. Determine the domain and range, to find the possible x value, take what is equal to y, for example y = square root of (25 - x²) , making it > than zero , has to equal to zero

   25 - x² >(equal to) zero
   25 >(equal to) x²

   x² <(equal to) 25
   Which means −5≤ x ≤5
   X intercepts are (5, 0) (-5, 0)

5. Determine possible y value, since there is a minus and y’s value, “must be less than or equal to 0” , y=− square root of 25−x²
   y = - square root of 25

   y = - 5 so y intercept is (0, -5)

6. Sketch the graph, its a circle so center is (0,0)