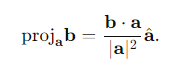The scalar product (1)
1/30
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
31 Terms
How is the magnitude of a vector calculated?
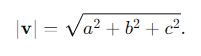
What does the magnitude of a vector represent?
It represents the size (or length) of the vector, which is the total displacement.
It is a scalar quantity.
What is a vector with a magnitude of 1 called?
A unit vector
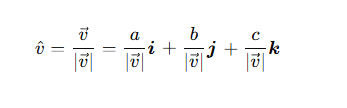
What is a unit vector?
Its a vector that has a magnitude of 1 and points in the same direction as the original vector.
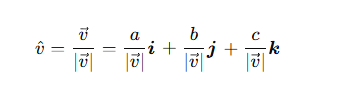
What does a unit vector show?
The direction of a vector
How is the unit vector in the direction of v=ai+bj+ck calculated?
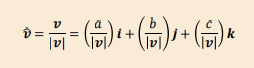
When are two vectors equal?
If and only if they have the same magnitude and the same direction.
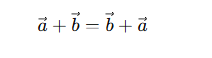
Is vector addition commutative?
Yes
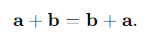
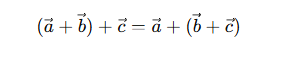
Is vector addition associative?
Yes

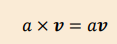
What happens when a vector is multiplied by a scalar?
It results in:
A vector in the same direction as the original.
A magnitude equal to the product of the magnitudes of the vector and the scalar.

What is a position vector?
A vector that describes the displacement of an object from the origin.
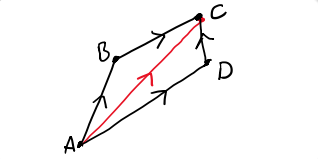
What does the parallelogram law of vector addition state?
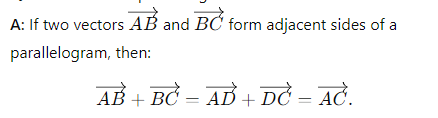
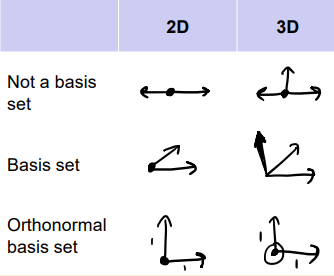
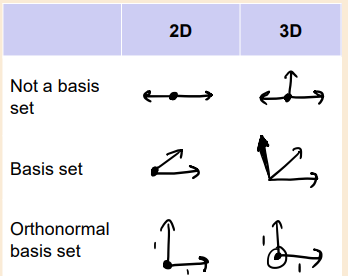
What are basis vectors in 2D?
They are two vectors that can be combined linearly to construct any vector on a 2D plane.
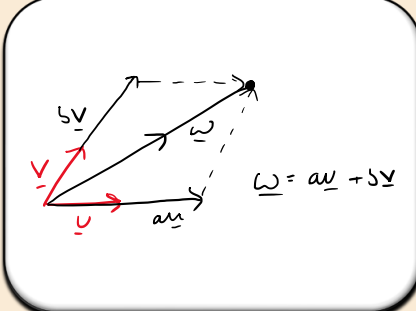
What is the condition for two vectors u and v to serve as basis vectors?
They must not be parallel (or antiparallel).
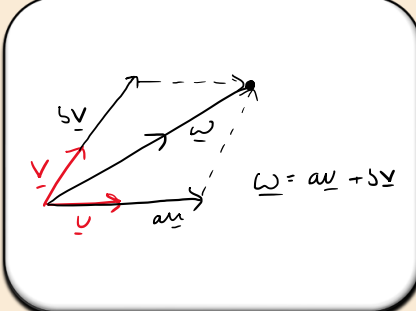
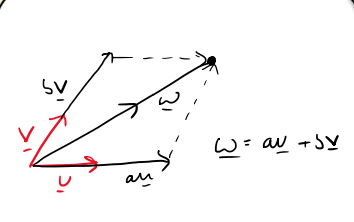
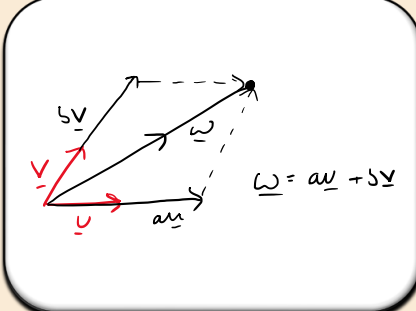
How can a vector w on the 2D plane be expressed using basis vectors u and v?

What is an orthonormal basis set?
A set of basis vectors that:
Have unit length 1 (normal)
Are mutually orthogonal (perpendicular to each other-at right angles to each other).
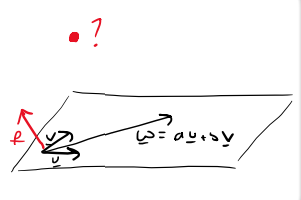
If 𝒘 = 𝑎𝒖 + 𝑏v can the set of w, u and v form a basis set in 3D?
No, because w, u and v lie on the same plane
Therefore their linear combinations can only form vectors on that plane, not in the full 3D volume.
What is required to form a 3D basis set?
A set of three vectors that are not coplanar.
What is the most convenient basis set in 3D?
The orthonormal set of vectors i, j and k also known as the Cartesian coordinates.
What does it mean for a set of vectors to be linearly dependent?
A set of vectors is linearly dependent if any vector in the set can be expressed as a linear combination of the others.
Can a linearly dependent set of vectors form a basis set?
No
What does it mean for a set of vectors to be linearly independent?
No vector in the set can be expressed as a linear combination of the others.
Can a linearly independent set of vectors form a basis set?
Yes
What is the criterion for linear independence in 3D for vectors u, v and w?
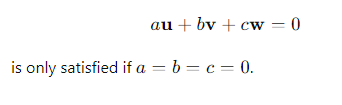
What are the two ways to "multiply" vectors?
Scalar (dot) product - gives a scalar.
Vector (cross) product - gives a vector.
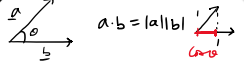
What is the scalar product (dot product) of two vectors a and b?
θ= the angle between the two vectors placed tail-to-tail.
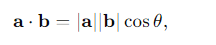
What does the scalar product represent when b is a unit vector?
It gives the length of the shadow of a in the direction of b.
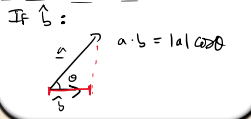
What does the scalar product represent when b is not a unit vector?
It gives the length of the shadow of a in the direction of b, multiplied by the magnitude of b.
What is the condition for two vectors to be perpendicular using the scalar product?
Two vectors are perpendicular if their scalar product is zero because the angle θ=π/2
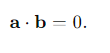
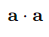
What is the scalar product of a vector with itself?
since the angle between a vector and itself is θ=0.
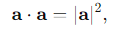
What is the formula for the projection of vector b onto vector a?
The projection of b in the direction of a is: