Unit 1 | Chapter 2: Set Theory

Set

A collection of objects whose contents can be clearly determined.

Elements/members

The objects in a set.

Word description

• A method for representing sets

• Can designate or name a set

• Ex: Set W is the set of days of the week.

Roster method

• A method for representing sets

• Lists the members of a set

• Ex: W= {Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday}

Set-builder notation

• A method for representing sets

• Explains the properties that its members must satisfy

• Ex: W = {x | x is a day of the week}

Empty/null set

• The set that contains no elements.

• Is a subset of every set.

  • Is ⊆ B, for any set B.

  • Is ⊂ B, for any set B other than the empty set.

{ } or Ø

Notation used to indicate that the set contains no elements.

∈

• Notation used to indicate that an object is an element of a set.

• It replaces the words, "is an element of."

∉

• Notation used to indicate that an object is not an element of a set.

• It replaces the words, "is not an element of."

The set of natural numbers

N={1, 2, 3, 4, 5, ...}

Ellipsis

The three dots after an element that indicates that there is no final element and that the list goes on forever unless shown to have an end.

≤ and < 

"Less than or equal to" and "Less than"

≥ and >

"Greater than or equal to" and "Greater than"

Cardinal number

• The number of set A is the number of distinct elements in set A.

• Represented by n(A), read "n of A."

• Is not changed by repeating elements

Equivalent set

• Set A and Set B contain the same number of elements.

• n(A) = n(B).

• If a set is equal, it is automatically equivalent.

then A is equivalent to B: n(A) = n(B).

If set A and set B can be placed in a one-to-one correspondence,

then A is not equivalent to B: n(A) ≠ n(B).

If set A and set B cannot be placed in a one-to-one correspondence,

Finite set

• A set whose cardinality is 0 [n(A) = 0, A is the empty set] or a natural number.

• Has a beginning and an end.

Infinite set

• A set whose cardinality is not 0 or a natural number.

• Has a beginning but no end.

Equality of sets

• Set A and Set B contain exactly the same elements, regardless of order or possible repetition of elements.

• Expressed as A = B.

• If a set is equal, it is automatically equivalent.

Subset of a set

• If every element in set A is also an element in set B.

• A ⊆ B.

• Every set is a subset of itself.

Not a subset of a set

• If there is at least one element of set A that is not an element of set B.

• A ⊄ B.

Proper subset

• If set A is a subset of set B and sets A and B are not equal (A≠B).

• Expressed as A ⊂ B.

Number of subsets

• The number of distinct subsets of a set

• n elements, 2ⁿ.

• As we increase the number of elements in the set by one, the number of subsets doubles.

Number of proper subsets

The number of distinct proper subsets of a set with n elements is 2ⁿ - 1.

Universal set

• A general set that contains all elements under discussion.

• U

• Represented by a rectangle

• Subsets within the universal ser are depicted by circles, or sometimes ovals, or other shapes.

John Venn

• 1843-1923

• Created Venn Diagrams to show the visual relationship among sets.

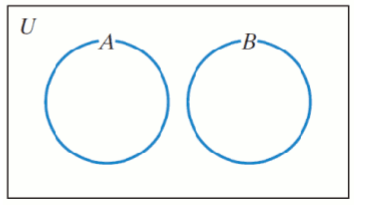
Disjoint sets

Two sets that have no elements in common.

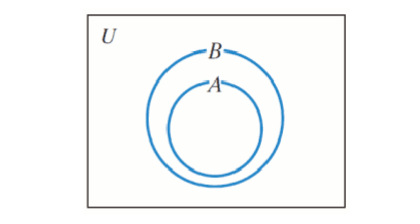
Proper subsets

All elements of set A are elements of set B.

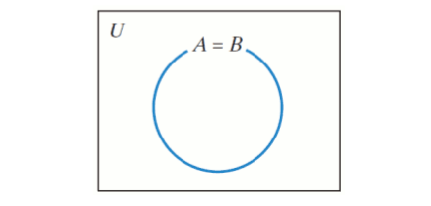
Equal sets

If A = B, then A ⊆ B and B ⊆ A.

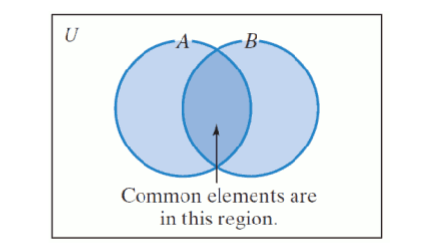
Sets with some common elements

If set A and set B have at least one element in common, then the circles representing the sets must overlap.

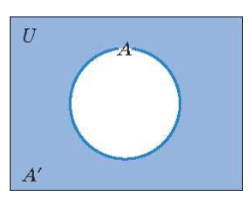
Complement of a set

• The set of all elements in the universal set that are not in A. Symbolized by A'.

• A ' = {x | x ∈U  and x∉A}.

• If you add it to its set, you get the universal set.

Intersection of sets

• The set of elements common to both set A and set B.

• And

• A∩B =  {x | x∈A  and x∉B}.

• A∩B

Union of sets

• The set of elements that are members of set A or of set B or of both sets.

• A∪B.

• A∪B =  {x | x∈A  or x∈B}.

• Or

A

A ∪ Ø = ?

Ø

A ∩ Ø = ?

always begin by performing any operations inside the paretheses.

When performing set operations with parentheses,

its best to start with the innermost part and move outward.

When filling a Venn diagram,

Or

Refers to the union of sets.

And

Refers to the intersection of sets.

n(A ∪ B) = n(A) + n(B) - n(A ∩ B)

Formula for the cardinal number of the union of two finite sets