A&A SL: Core Topics: Statistics

A&A SL Core Textbook Chapter 12 Lessons A-J

Standard Deviation

• a form to more accurately represent the spread of data

• the square root of the variance

• measures the degree to which the data deviates from the mean

• a non-resistant measure of spread

• only useful if the data is symmetrical

• if a sample from a large population the sample standard deviation (s) is a more accurate estimate

Variance

• represents a more accurate spread of data

• the average of the squares of the distances from the mean

• If data values (xᵢ) are situated close around the mean (μ) then (xᵢ - μ)² would be too small and have too small of a variance

Percentiles

• the values below which a certian percentage of the data lies

  • Q1 is the 25th percentile

  • Q2 is the 50th percentile

  • Q3 is the 75th percentile

Frequency Graph

• made of the cumulative frequency

• a smooth graph with curves

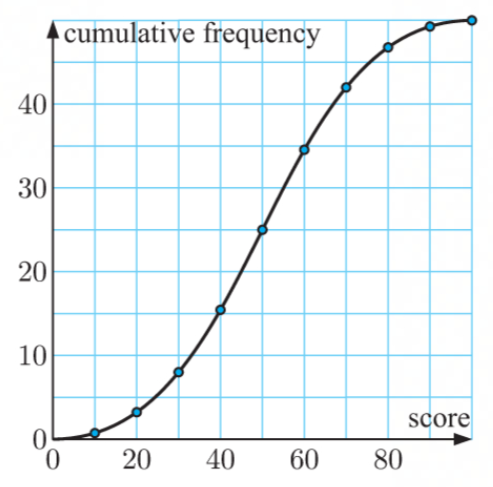
Cumulative Frequency

• shows the number/proportion of numbers that lie above or below a particular value

• can create column for the cumulative frequency within a frequency table

• will create a frequency graph which create a graph of smooth curves

parallel box and whisker diagram / parallel box plot

• a visual comparison of the distribution of two data sets

• used to easily compare statistics such as the median, range, and IQR

Outliers

• extraordinary data separated from the main body of data

• applies to any value larger or smaller than the boundaries

  • upper boundary = upper quartile + 1.5 x IQR

  • lower boundary = upper quartile + 1.5 x IQR

• outliers are marked with an Astrid on a Wisker box plot

• it is possible to have more than one outlier

negatively skewed box plot

positively skewed box plot

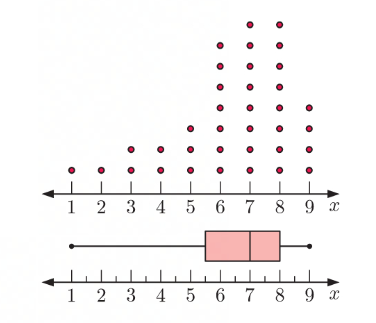
symmetrically distributed box plot

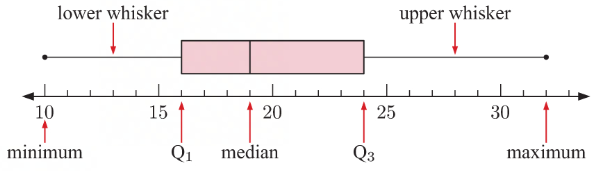
Five Number Summary

• made up of:

  • the minimum value

  • the lower quartile Q1

  • the median Q2

  • the upper quartile Q3

  • the maximum value

Box and Whisker diagram / Box Plot

• will show the five number summary of the data set

• rectangular box represents the “middle“ half

• lower whisker shows the 25% smallest values

• upper whisker shows the 25% largest values

• shows the systematic distribution of a box plot

Interquartile range

• AKA: IQR

• the median divides the ordered set into halves and then in half again by quartiles

• IQR = Q3 - Q1

• Lower Quartile (Q1)

  • middle value of the lower half

• Upper Quartile (Q3)

  • middle value of the upper half

• Interquartile range (IQR) (Q2)

  • the range of the middle half of data

The Range

• the difference between the maximum data value and the minimum data value

• Range = maximum - minimum

• not particularly reliable as it only uses two data values

• easily influenced by extreme values and outliers

• useful for choosing class intervals

approximation

• calculated mean represents the approximated value

• reason to why you need to know each individual data value

• a result of assuming data values within classes

midpoint / mid-interval value

• a representation of all data values in a class interval

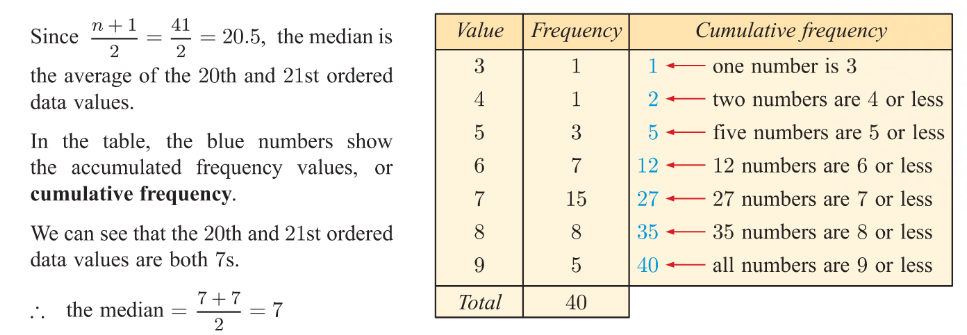
finding the median

solving for the mean

product column

• helps to add the data values

frequency column

• found in a frequency table

• used to easily find the mode

median characteristics

• gives data a halfway point

• only accounts for middle values

• not affected by extreme values

mean characteristics

• commonly used and easy to understand

• accounts for all values

• affected by extreme values

mode characteristics

• gives the most usual value

• only accounts for common values

• unaffected by extreme values

bimodal

• when a data set has two values that occur most frequently

center of the data

• measured with the mean, median, and mode

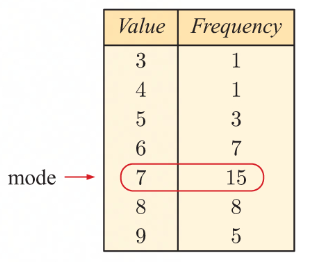
mode

• most frequently occurring value in a discrete data set

• the modal class in continuous data sets

• if a data set has two values that both occur most frequently it is bimodal

• if the data set has three or more most frequently occurring values the mode becomes inapplicable

median

• middle value of an ordered data set

• splits data in half

  • EX: the median mark for a test is 73% then you know that half the class scored less than or equal to 73% and half the class scored greater than or equal to 73%

• if there is an odd number of data values the median is one of the original values

• if there is an even number of data values then the median will be the average of the two middle numbers

• if there are n data values listed in order from smallest to largest the median is the (n+1/2)th data value

mean

• the statistical name for an arithmetic average

• mean = the sum of all data values / the number of data values

• use ˉx to represent the mean of a sample

• use μ to represent the mean of a population

  • you do not always have data from all the population members so the exact value of μ is unknown

  • collect data from a sample of a population and use the mean of the sample ˉx as an approximation for μ