feb 25 lecture binomial distribution

Bernoulli random variables

• a Bernoulli distribution is a discrete probability distribution of a random variable with only 2 possible outcomes (binary or dichotomous variable)

  • Will also have mutually exclusive and exhaustive outcomes

  • The outcomes take the value 1 with probability p and the value 0 with probability 1-p

    → We can define the probability mass function as:

Bernoulli distribution

Binomial random variables

• examine a random binary outcome over multiple independent Bernoulli trials

  • 1 trial → Bernoulli

  • 2+ trial → binomial

If there are n (number of trial) independent Bernoulli trials, each of
which has a probability of “success” p (proabability), we can let
X denote the total number of successes observed
in n trials

binomial parameters & assumptions

factorials

A factorial is the number of different ways to
order n distinctive subjects
▪ Formula: n! = n(n − 1)(n − 2) ···(3)(2)(1)
▪ Example: 5! = 5*4*3*2*1 = 120
▪ By definition, 0! is equal to 1

combinations

A combination is the number of different ways to pick x subjects out of a total of n subjects without regard to order

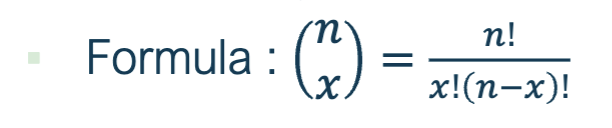
factorial and combination example 1

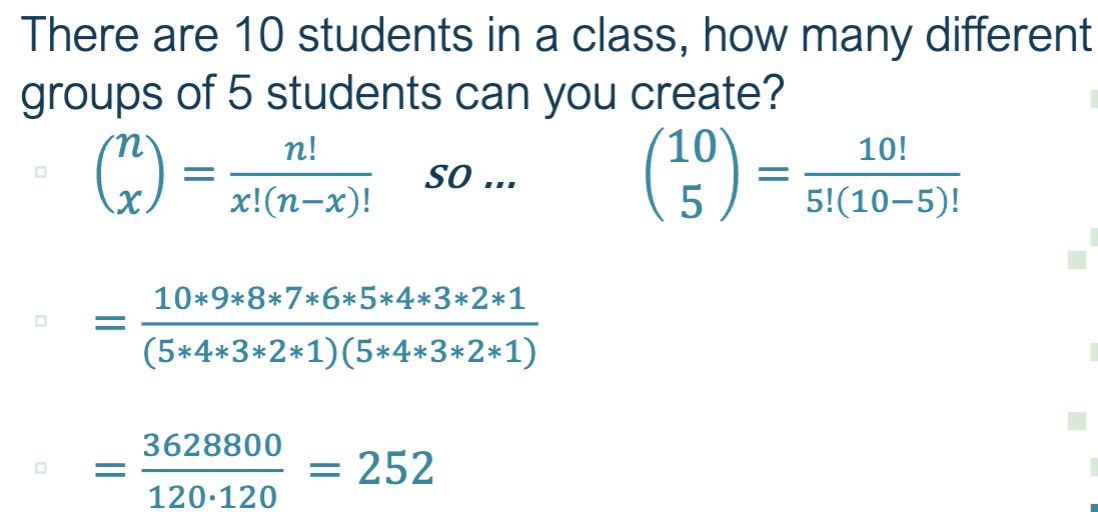
combination example 2 - in order

binomial probability mass function

• The probability of observing X= k successes out
  of n independent trials is given by the probability
  mass function

• last formula is the most important

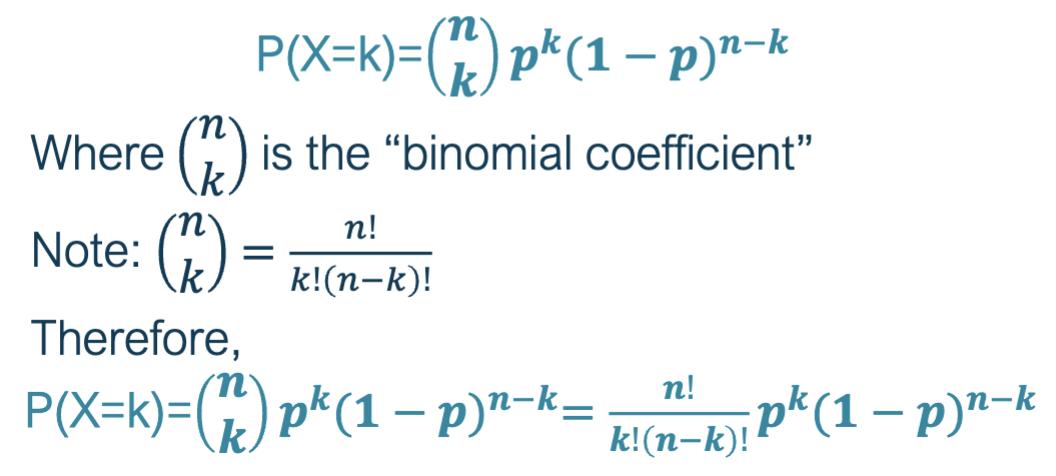
Binomial PMF Example

their chances of being flu positive: .137

binomial cumulative distribution function (Binomial CDF)

• the CUMULATIVE distribution function of a binomial random variable

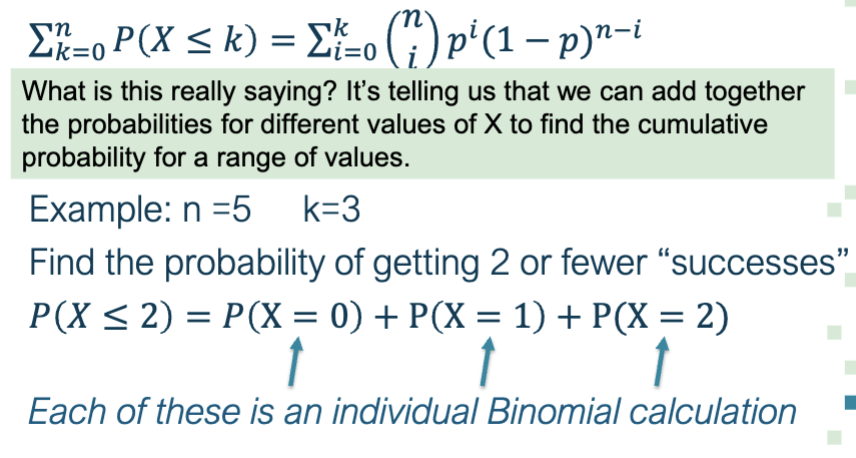
binomial cumulative value - methods

• For binomial random variables, combined probabilities can be generated in 2 ways:

  1. Direct method: If examining a small range of probabilities, you may sum each probability

  2. Indirect method: If examining a large range, sum the probabilities NOT included in your range, and subtract from 1(the compliment)

     → Be very aware of the range for your question(e.g. less than, more than, at least, at most)

binomial CDF example - with indirect and direct method

• x=2 through x=6 would have had to calculated beforehand

.834 = 1 or fewer

→ COMPLEMENT RELATIONSHIP (1-P)

*2 out of 6 - finding the complement = 1 or fewer

bin distribution mean and variance and example

• specifically binomial random variables:

  • mean = np (AKA: expected number of successes)

  • variance = np(1-p)

---

→ EXAMPLE:

1. expected number of positive flu tests (mean)