1.8/1.9/1.10 rational functions and vertical asymptotes and holes + rational functions and zeros

F(x) as x —> b+

F(x) gets larger and closer to positive infinity because x valued are decreasing towards b and smaller numbers gives larger outputs.

f(x) as x —> b-

f(x) gets smaller and closer to negative infinity because as x values are increasing towards b smaller outputs are produced

Vertical asymptote definition

f(x) increases or decreases without bound as x approaches b from the left and right

where a vertical asymptote occurs

When the multiplicity of a common factor is greater in the denominator

There are real roots in the denominator that aren’t there in the numerator

The unique characteristic of vertical asymptotes

makes the function undefined and the outputs increase/decrease without bound

Hole definition

when the function is not continuous

characteristics of a functions with holes

there is a common factor in the numerator and denominator

The multiplicity of a common factor is greater in the numerator

Characteristics of both holes and vertical asymptotes

Both are located at undefined places

Holes in a rational function algebraically

in numerators and denominators with the same multiplicity that cancel out

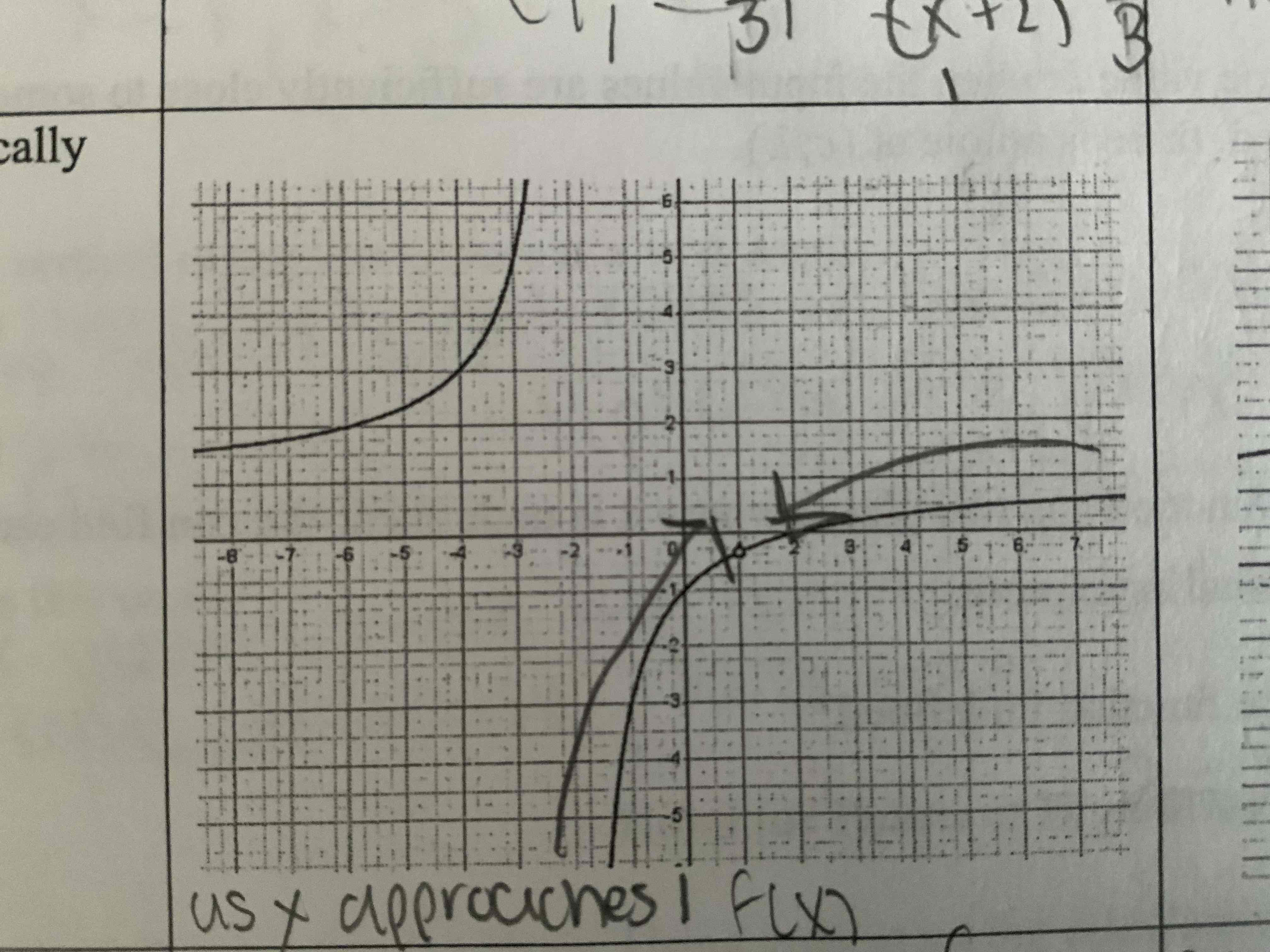
holes graphically

Image

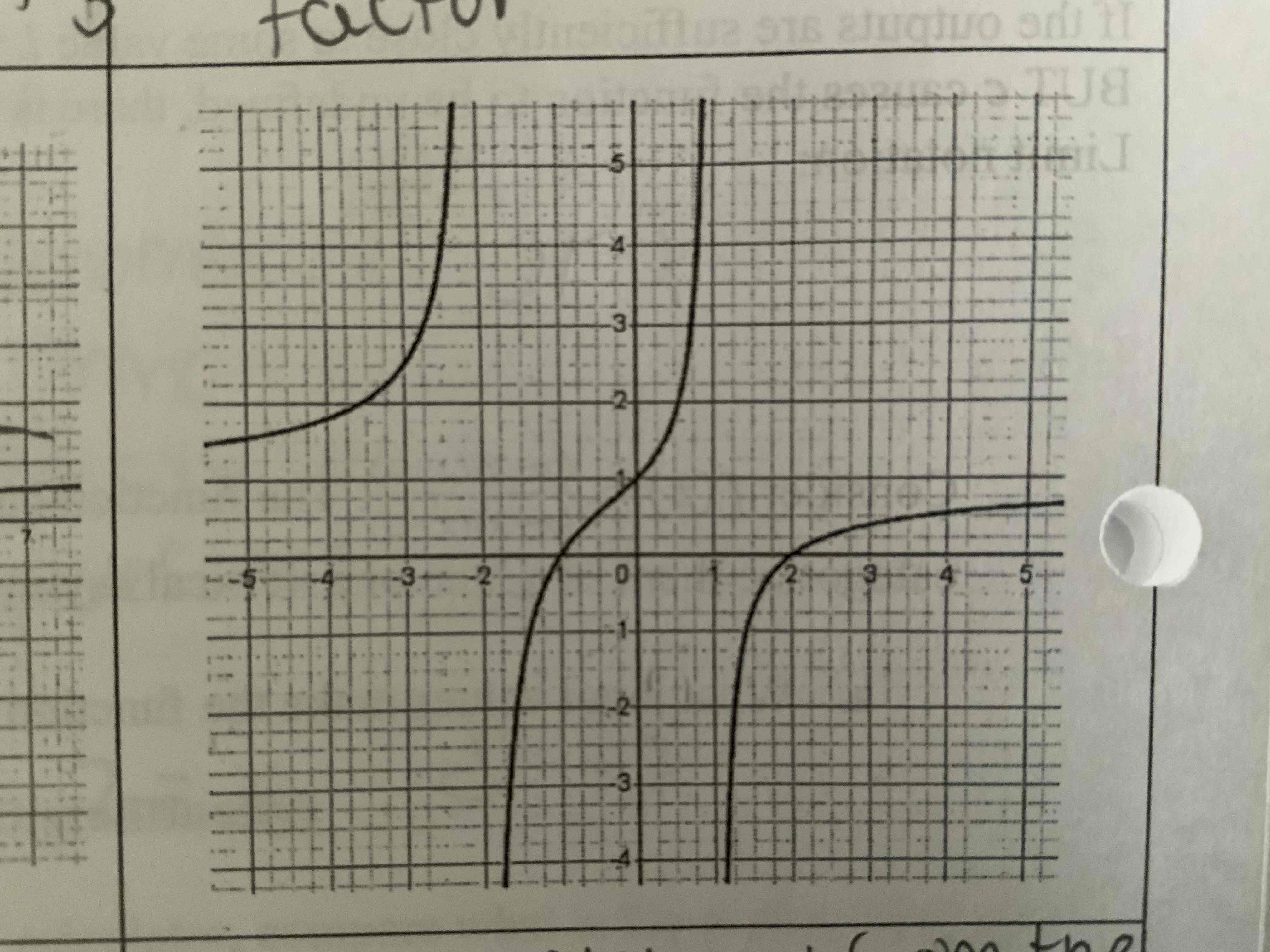
vertical asymptotes graphically

image

holes verbally

As x approaches x value of hole f(x) approaches y value of hole

Vertical asymptotes verbally

As x approaches b from the left g(x) increases without bound

as x approaches b from the right g(x) decreases without bound

limit notation from hole

image

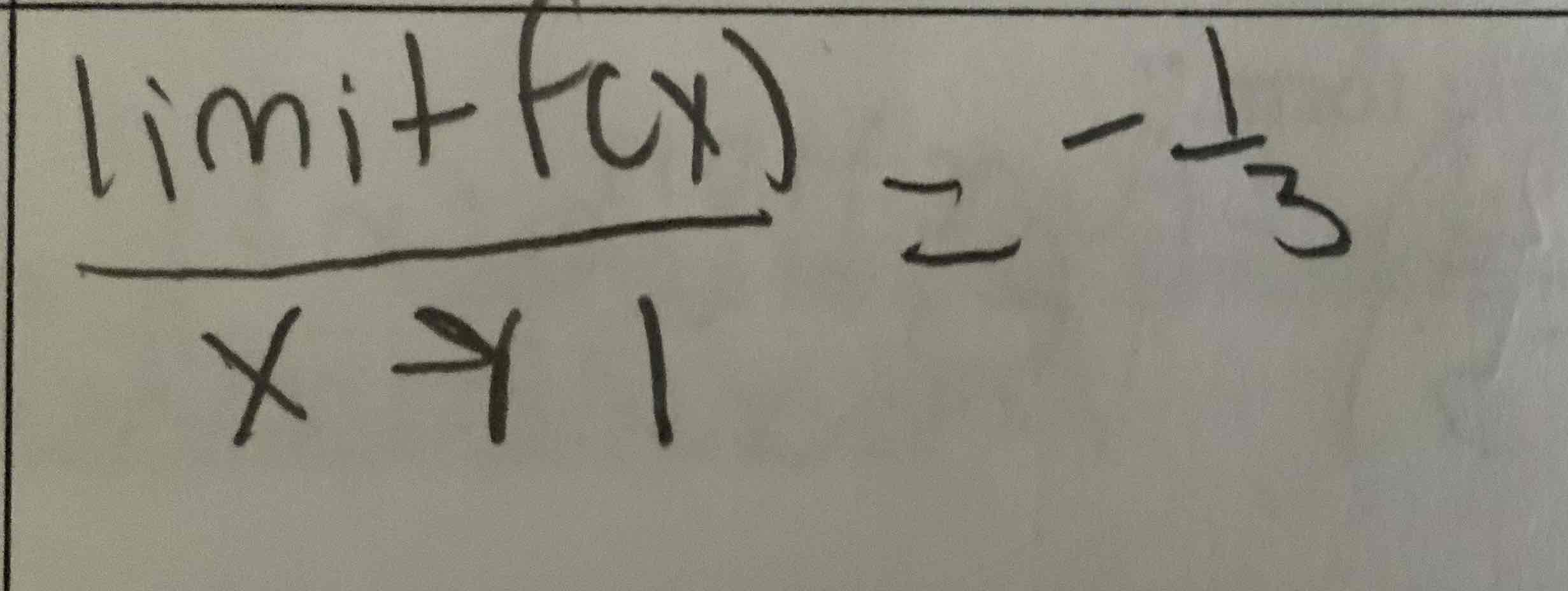
limit notation of vertical asymptote from left

limit g(x) = inifinity

x —> b-

limit notation of vertical asymptote from right

limit g(x) = - infinity

x —> 1+

Zeros of a numerator

Roots of a rational function in algebraic form

Zeros of a denominator

Vertical asymptotes of a rational function in algebraic form