Trig Substitution and Trig Integrals

1 + tan² θ

cot² θ + 1

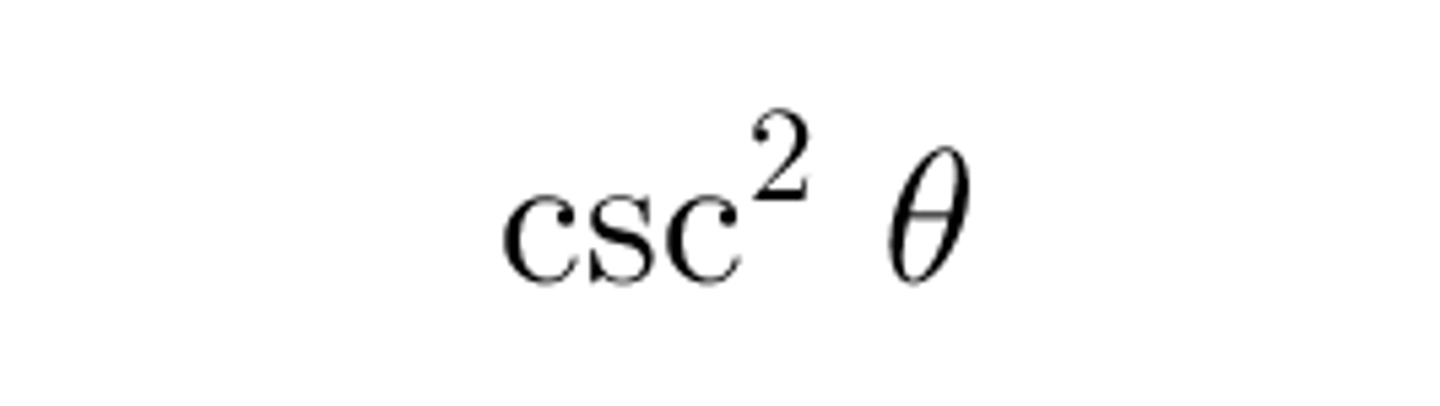
tan θ

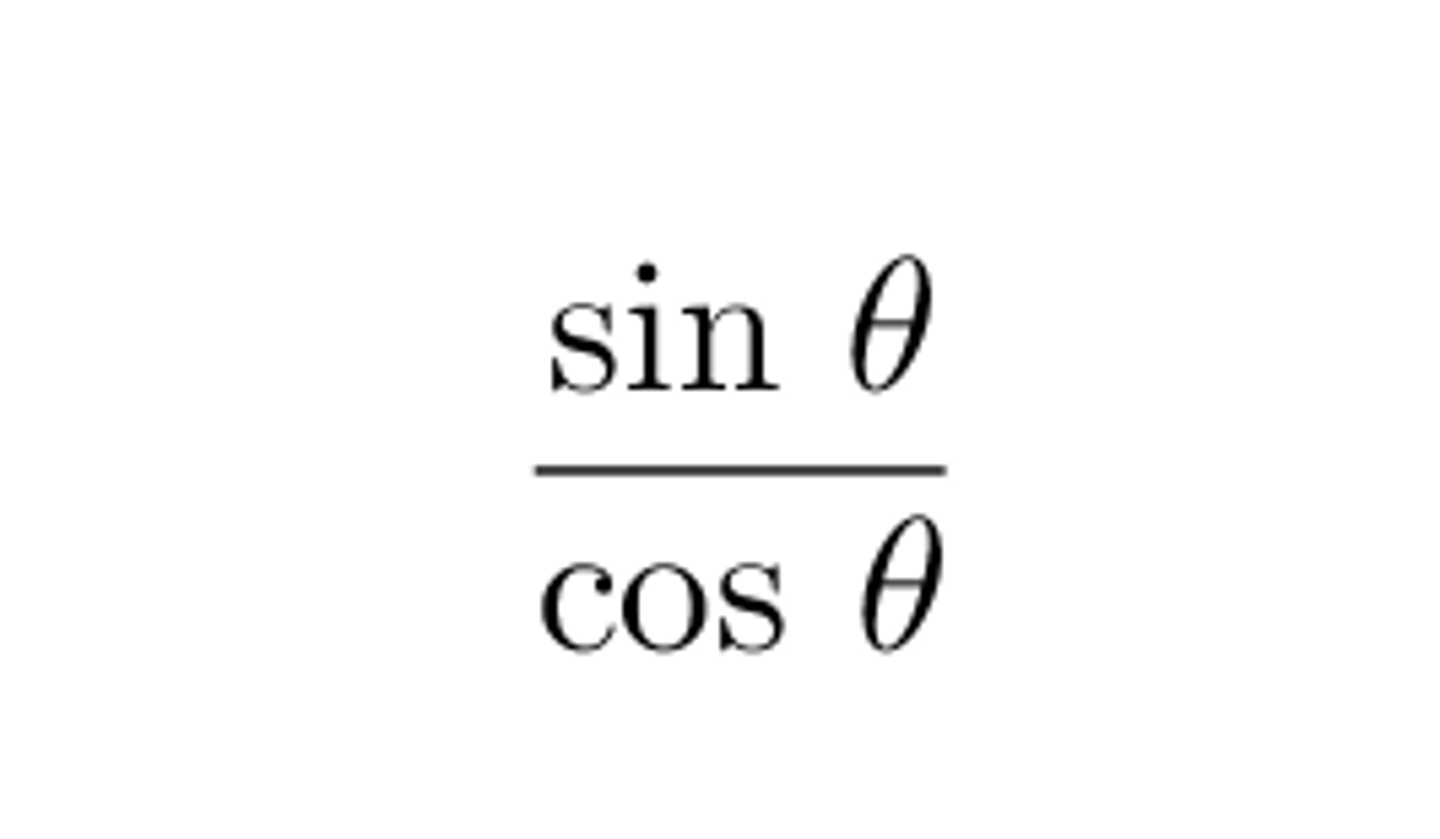
cot θ

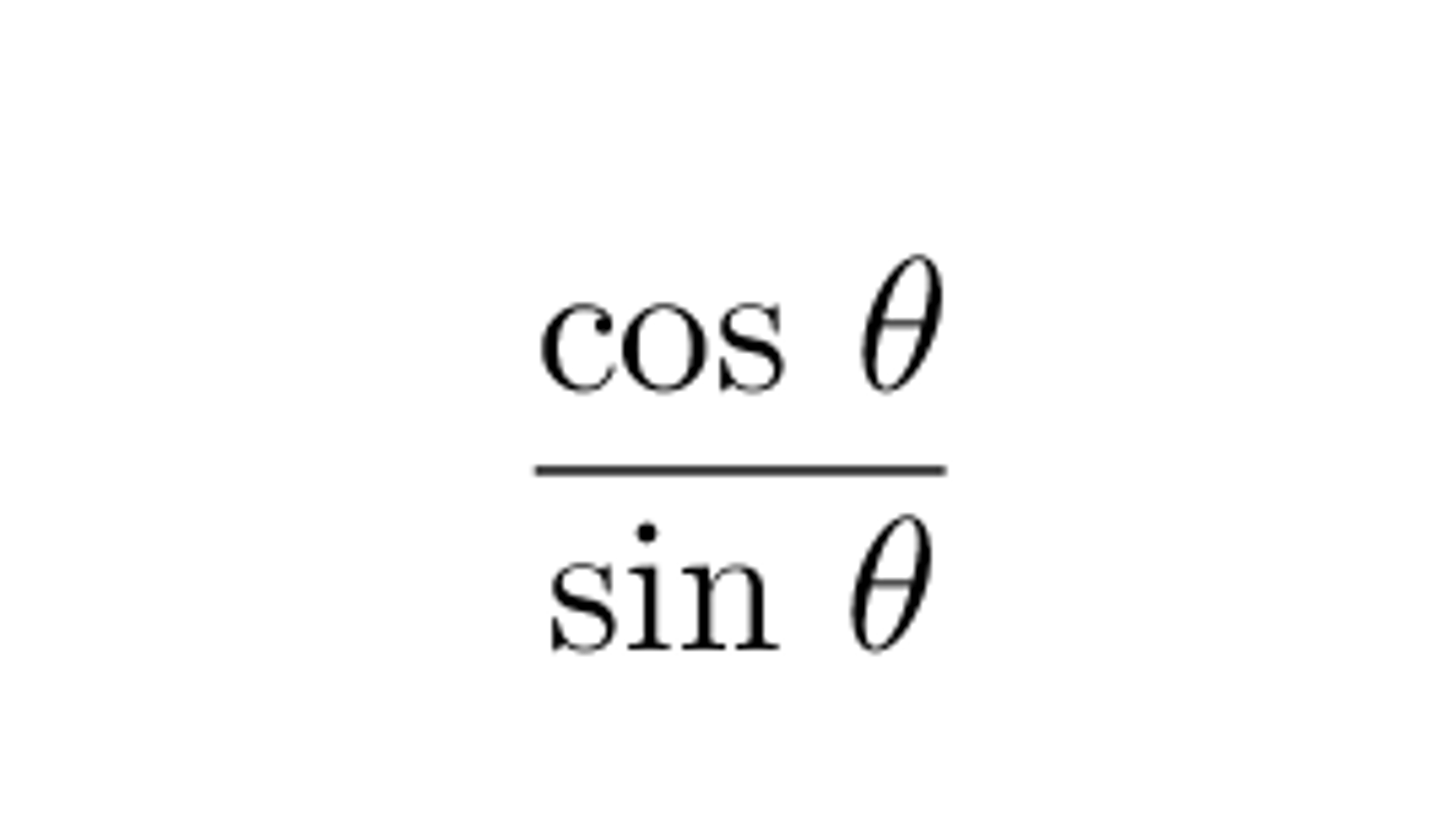
1

sec² θ - tan² θ =

cot² θ

csc² θ - 1

sin²θ+cos²θ=?

1

(double angle formula)

sin²x =

(1-cos2x)/2

(double angle formula)

cos²x =

(1+cos2x)/2

sinmxsinnx =

(1/2) [cos((m-n)x) - cos((m+n)x)]

sinmxcosnx =

(1/2) [sin((m-n)x) + sin((m+n)x)]

cosmxcosnx =

(1/2) [cos((m-n)x) + cos((m+n)x)]

dx sinθ

cosθ

dx cosθ

-sinθ

∫sinθ

-cosθ

∫cosθ

sinθ

∫sec²xdx

tanx+c

∫tan²xdx

tanx - x +c

∫secx dx

ln|secx + tanx| + c

∫tanxdx

-ln|cosx|+c

x = asinθ

dx = acosθ

√a²-u²

use x = asinθ

x = atanθ

dx = asec²θ

√a²+u²

use x =atanθ

x = asecθ

dx = asecθtanθ

√u²-a²

use x = asecθ

(Trig integrals)

When integrating sinx/cosx functions that have only even powers use the double angle identities to substitute

Example: ∫cos²dx = ∫((1+cos2x)/2)dx

Example: ∫cos²xsin²xdx = ∫((1+cos2x)/2)((1-cos2x)/2)dx

How to solve sinx/cosx functions that only have even powers

(Trig integrals)

When integrating tanx/secx functions that have only even powers use the (sec²x-tan²x = 1) identity to substitute OR use integration by parts

Example: ∫sec³xdx <- integration by parts

Example: ∫tan²xsec⁴xdx <- sec²x = tan²x+1

How to solve tanx/secx functions that only have even powers

Completing the square

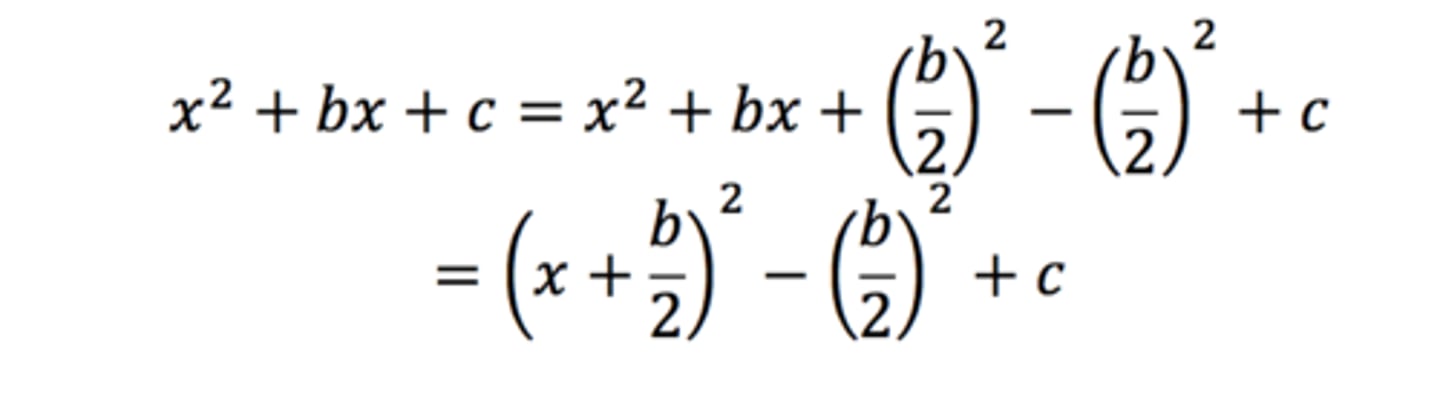
trig triangle relations

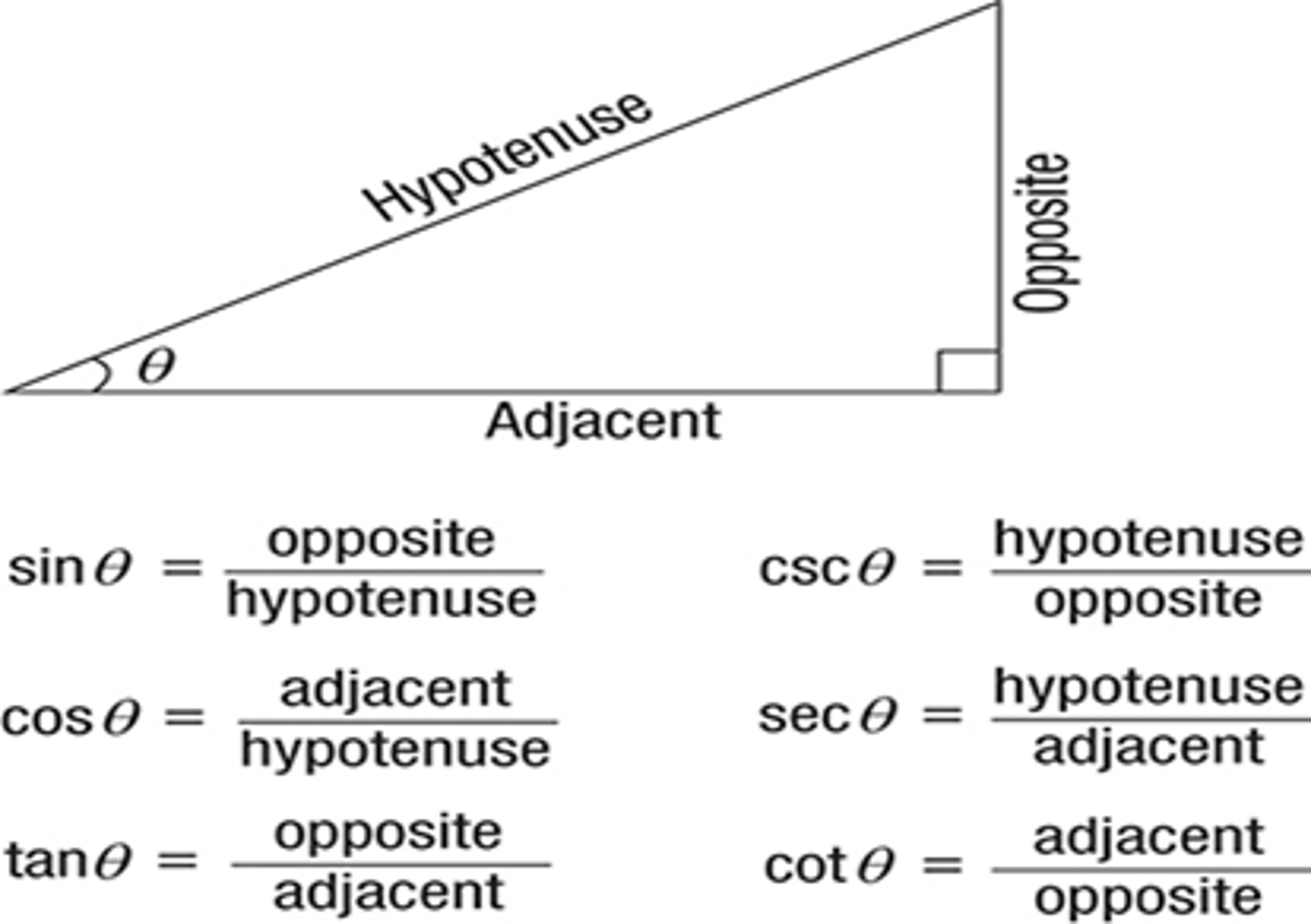
(Trig integrals)

When integrating a trig function that contains a function to the odd power

Example: ∫sin³xdx

Example: ∫cos⁵xsin²xdx

Split it into a squared function and a single power function then use (sin²x = 1-cos²x) or (cos²x = 1-sin²x) to sub the squared power.

How to solve trig functions that have any odd powers