K-Means and Hierarchical Clustering
0.0(0)
Card Sorting
1/28
There's no tags or description
Looks like no tags are added yet.
Last updated 2:16 PM on 5/15/23
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
29 Terms
1
New cards
K-means
Iterative greedy descent algorithm that finds a sub-optimal solution to
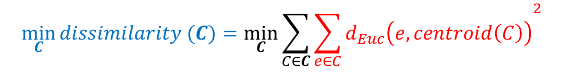
2
New cards
K-means iteratively alternates between the following two steps:
• Assignment step: For given set of K cluster centroids, K-means assigns each example to the cluster with closest centroid.
* fix centroids and optimize cluster assignments (optimizes the red highlighted part).(optimizes the red highlighted part)
• Refitting step: Re-evaluate and update the cluster centroids, i.e., for fixed cluster assignment, optimize the centroids
* fix centroids and optimize cluster assignments (optimizes the red highlighted part).(optimizes the red highlighted part)
• Refitting step: Re-evaluate and update the cluster centroids, i.e., for fixed cluster assignment, optimize the centroids
3
New cards
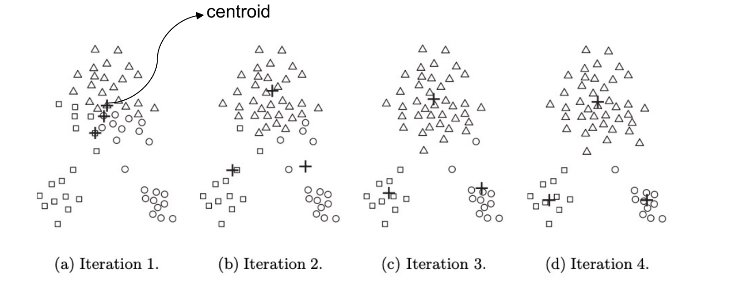
K-Means Algorithm

4
New cards
Space Complexity of K-Means
Space requirement for K-means is modest because only data observations and centroids are stored
Storage complexity is of the order O((N+ K)m), where m is the number of feature attributes
Storage complexity is of the order O((N+ K)m), where m is the number of feature attributes
5
New cards
Time Complexity of K-Means
ime complexity of K-means: O(I\*K\*N\*m) where I is the number of iterations required for convergence
Importantly, time complexity of K-means is linear in N.
Importantly, time complexity of K-means is linear in N.
6
New cards
Does the K-means algorithm always converge?

7
New cards
Can it always find optimal clustering?
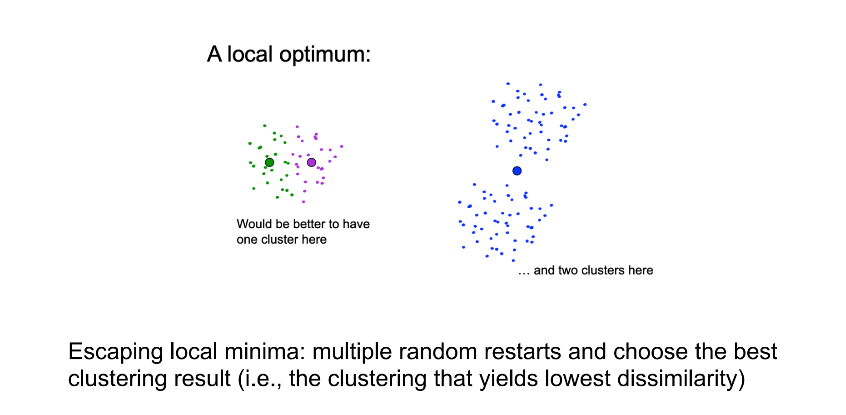
8
New cards
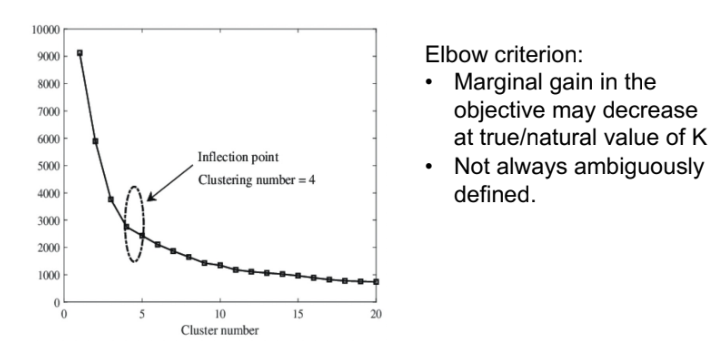
How should we choose the number of clusters?
Run multiple K-means algorithm starting from randomly chosen cluster centroids. Choose the cluster assignment that has the minimum dissimilarity. using the elbow method
9
New cards
K-means++
\- Choose first centroid at random.
\- For each data point x compute its distance dist(x) from the nearest centroid.
\- Choose a data point x randomly with probability proportional to dist(x)^2 as the next centroid.
- Continue until K cluster centroids are obtained.
- Use the obtained K centroids as initial centroids for the K-means algorithm
\- For each data point x compute its distance dist(x) from the nearest centroid.
\- Choose a data point x randomly with probability proportional to dist(x)^2 as the next centroid.
- Continue until K cluster centroids are obtained.
- Use the obtained K centroids as initial centroids for the K-means algorithm
10
New cards
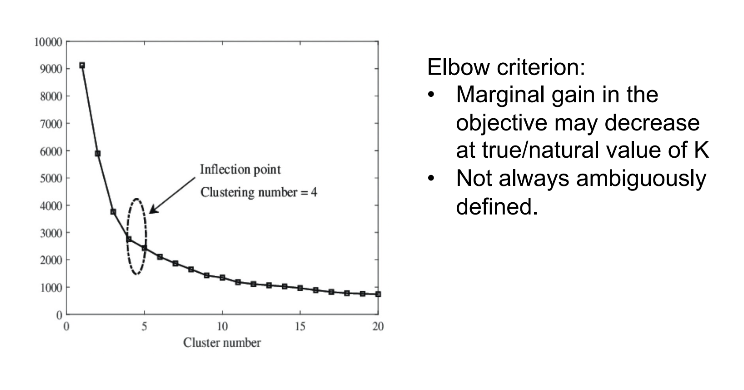
Elbow method
o Apply K-means algorithm multiple times with different number of clusters.
o Evaluate the quality of the obtained clustering structure in each run of the algorithm using the metric dissimilarity(C) .
o As the number of clusters increases, dissimilarity(C) tends to decrease.
o Plot dissimilarity(C) as a function of the number K of clusters.
o Optimal K\* lies at the elbow of the plot.
o Evaluate the quality of the obtained clustering structure in each run of the algorithm using the metric dissimilarity(C) .
o As the number of clusters increases, dissimilarity(C) tends to decrease.
o Plot dissimilarity(C) as a function of the number K of clusters.
o Optimal K\* lies at the elbow of the plot.
11
New cards
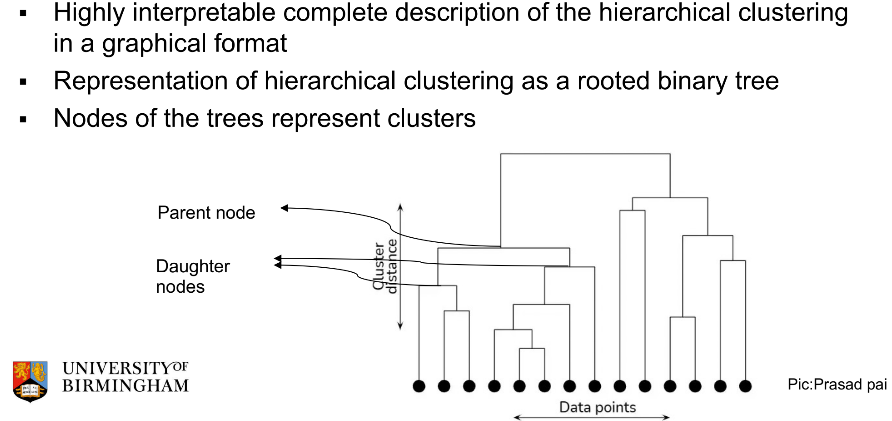
hierarchical clustering
user specifies a measure of similarity (or dissimilarity) between a pair of clusters - it creates a hierarchical decomposition of the set of examples using a user-specified criterion and produces a dendrogram
12
New cards
Dendrogram
13
New cards
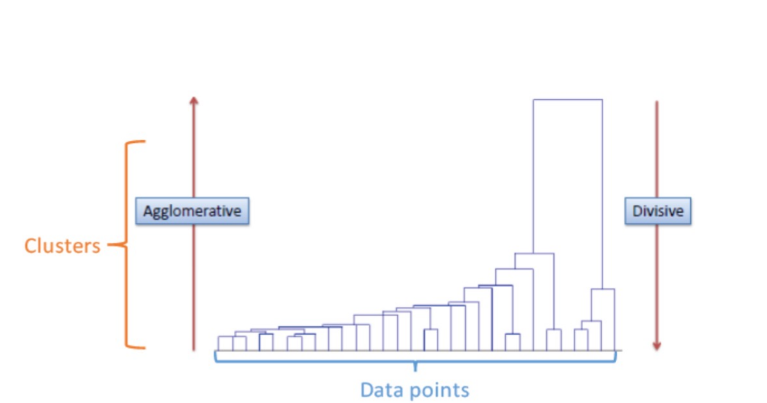
Strategies for Hierarchical Clustering
Agglomerative Clustering and Divisive Clustering
14
New cards
Agglomerative Clustering
* Bottom-up approach
* Starts at the bottom with each cluster containing a single observation
* At each level up, recursively merge pair of clusters with the smallest inter-cluster dissimilarity into a single cluster.
* A single cluster at the top level
* Starts at the bottom with each cluster containing a single observation
* At each level up, recursively merge pair of clusters with the smallest inter-cluster dissimilarity into a single cluster.
* A single cluster at the top level
15
New cards
Divisive Clustering
* Top-down approach
* Starts at the top with a single cluster of all observations
* At each level down, recursively split one of the existing clusters into two new clusters with the largest inter-cluster dissimilarity.
* At the bottom, each cluster contains single observation
* Starts at the top with a single cluster of all observations
* At each level down, recursively split one of the existing clusters into two new clusters with the largest inter-cluster dissimilarity.
* At the bottom, each cluster contains single observation
16
New cards
Agglomerative Clustering Algorithm
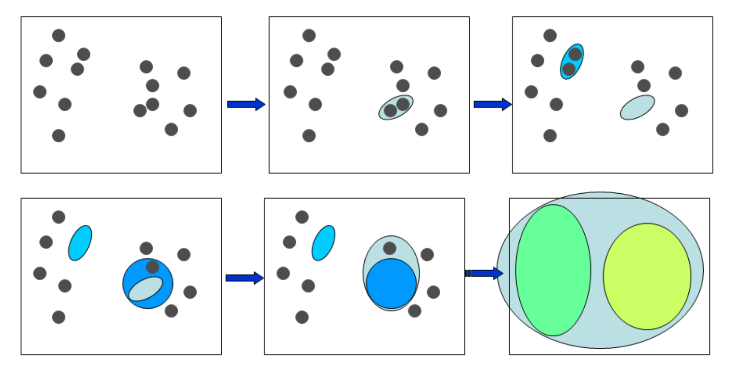
1\. Start with all data points in their own clusters.
2. Repeat until only one cluster remains:
* Find 2 clusters C1, C2 that are most similar (i.e., that have the smallest inter-cluster dissimilarity d(C1,C2) )
* Merge C1,C2 into one cluster
Output: a dendrogram
Reply on: an inter-cluster dissimilarity metric
2. Repeat until only one cluster remains:
* Find 2 clusters C1, C2 that are most similar (i.e., that have the smallest inter-cluster dissimilarity d(C1,C2) )
* Merge C1,C2 into one cluster
Output: a dendrogram
Reply on: an inter-cluster dissimilarity metric
17
New cards
Measures of Inter-Cluster Dissimilarity
Single linkage, Complete linkage and Group average
18
New cards
Single linkage
Shortest distance from any member of the cluster to any member of the other cluster

19
New cards
Complete linkage
Largest distance from any member of the cluster to any member of the other cluster

20
New cards
Group average
Average of distances between members of the two clusters
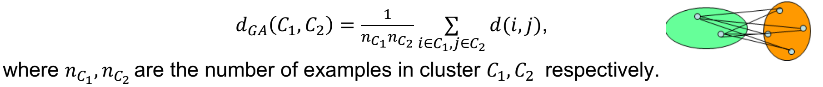
21
New cards
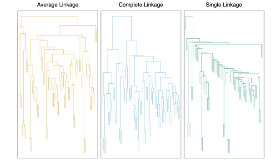
Does the choice of inter-cluster dissimilarity measure matter?
• Yes !!!
• Yields similar results when the (natural) clusters are compact and well-separated
• Yields similar results when the (natural) clusters are compact and well-separated
22
New cards
Single linkage advantage and disadvantage
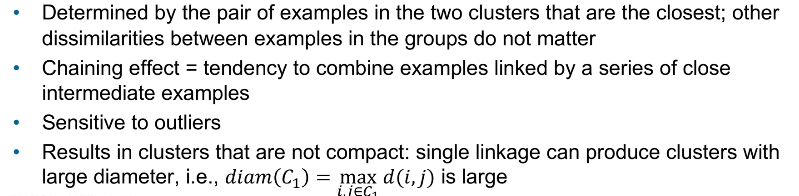
23
New cards
Complete linkage advantage and disadvantage
• Requires all examples in the two clusters to be relatively similar
• Produces compact clusters with small diameters
• Robust to outliers
• However, members can be closer to other clusters than they are to members of their own clusters
• Produces compact clusters with small diameters
• Robust to outliers
• However, members can be closer to other clusters than they are to members of their own clusters
24
New cards
Group average linkage advantage and disadvantage
• Attempts to produce relatively compact clusters that are relatively far apart
• Depends on the numerical scale on which the distances are measured
• Depends on the numerical scale on which the distances are measured
25
New cards
Space complexity of Hierarchical Clustering

26
New cards
Time complexity of Hierarchical Clustering

27
New cards
Characteristics of Hierarchical Clustering
* Lack of a global objective function
• Need not solve hard combinatorial optimization problem as in K-means
• No issues with local minima or choosing initial points
* Deterministic algorithm
* Merging decisions are final
* May impose a hierarchical structure on an otherwise unhierarchical data
• Need not solve hard combinatorial optimization problem as in K-means
• No issues with local minima or choosing initial points
* Deterministic algorithm
* Merging decisions are final
* May impose a hierarchical structure on an otherwise unhierarchical data
28
New cards
Advantages of K-means
• Optimizes a global objective function
• Squared Euclidean distance based
• Non-deterministic
• Squared Euclidean distance based
• Non-deterministic
29
New cards
disadvantages of k-means
• Requires as input: number of clusters and an initial choice of centroids
• Convergence to local minima implies multiple restarts
• Convergence to local minima implies multiple restarts