AP Precalculus - Fall Final Exam - Equations

Which axis does this reflect across: -(x)?

y-axis

Which axis does this reflect across: (-x)?

x-axis

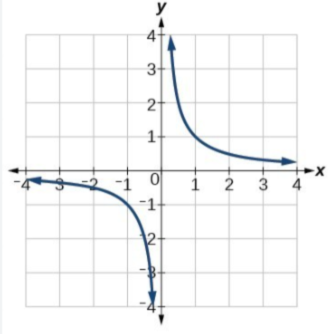
Which graph is this?

y = 1/x (reciprocal)

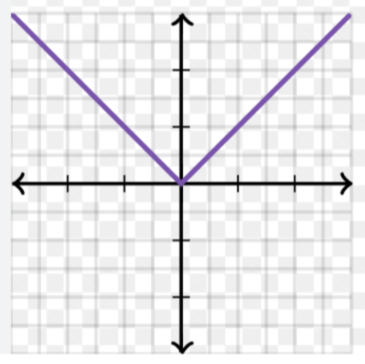
Which graph is this?

y = |x|

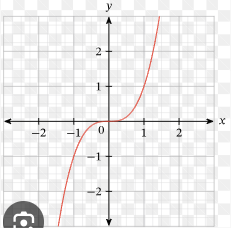
Which graph is this?

y = x³

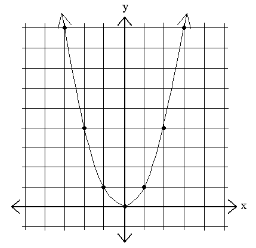
Which graph is this?

y = x²

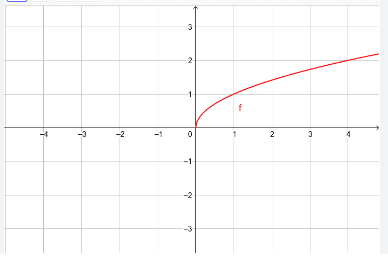
Which graph is this?

y = √x

A² + B² = ?

(A + B)(A - B)

A² + 2AB + B² = ?

(A + B)²

A² - 2AB + B² = ?

(A - B)²

A³ + B³ = ?

(A + B)(A² - AB + B²)

A³ - B³ = ?

(A - B)(A² + AB + B²)

if A > 1, Ax² + Bx + C =?

(A1x + C1)(A2x + C2) remember, that A = A1 x A2; C = C1 x C2

Standard form quadratic function = ?

Ax² + Bx + C

Vertex form quadratic function = ?

A(x - h)² + k (h and k are the vertex (h,k))

Intercept form of quadratic function = ?

A(x - C1)(x - C2) (C1 & C2 are zeroes)

How do you find the vertex point (h, k)?

(-b/2a, f(-b/2a))

A function is even if ______

f(-x) = f(x)

A function is odd if ______

f(-x) = -f(x)

If the degree of the polynomial (n in a^n) is even and the leading coefficient is positive, then …

as x → ∞, f(x) → ∞ ; as x → -∞, f(x) → ∞ (up…up)

If the degree of the polynomial (n in a^n) is even and the leading coefficient is negative, then …

as x →∞, f(x) → -∞ ; as x → -∞, f(x) → -∞ (down…down)

If the degree of the polynomial (n in a^n) is odd and the leading coefficient is positive, then …

as x → ∞, f(x) → ∞ ; as x→ -∞, f(x) → -∞ (down…up)

If the degree of the polynomial (n in a^n) is odd and the leading coefficient is negative, then …

as x → ∞, f(x) → -∞ ; as x → -∞, f(x) → ∞ (up…down)

i = ?

i² = ?

i³ = ?

i^4 = ?

i^5 = ?

√-1, -1, -i, 1, i

How do you find the possible rational zeroes of each function?

p/q (p=A, q=C)

To find the number of positive real zeroes in a function, ____

see how many sign changes there are. (e.g. +x³ - x² + 3 has 2 (+) real zeroes)

To find the number of negative real zeroes in a function, ____ (this is called Descarte’s Rule of Signs)

flip all of the signs from + → - and - → +, and see how many sign changes there are. (e.g. change x² + 1 to -x² -1, and we see that there are 0 (-) real zeroes)

How do you find the upper bound of a polynomial?

How do you find the lower bound of a polynomial?

Upper Bound: do synthetic division on the polynomial with any random number. If all of the values are positive, then that number is the upper bound (doesn’t work if the remainder is 0).

Lower Bound: do synthetic division on the polynomial with any random number. If the values go consecutively from (+) to (-) or vise versa, that number is a lower bound (doesn’t work if the remainder is 0).

If n > m, ___

there is only a SLANT asymptote (you find it by doing synthetic division, and then you make that the value of the slant asymptote)

If n = m, ___

there is a HORIZONTAL asymptote (y = a/b) (a is the coefficient of the numberator) (b is the coefficient of the denominator)

If n < m, ___

the HORIZONTAL asymptote is y = 0

How do you find the vertical asymptote?

set the denominator to 0, and solve for x

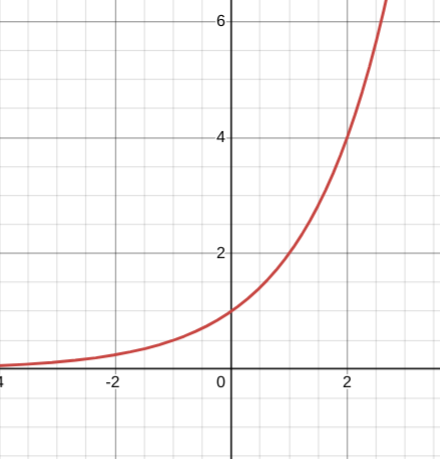
What graph is this?

y = 2^x

Equation for Compount Interest

A = P(1 + r/n)^nt

Equation for Half Life

A = Ao(1/2)^t/h

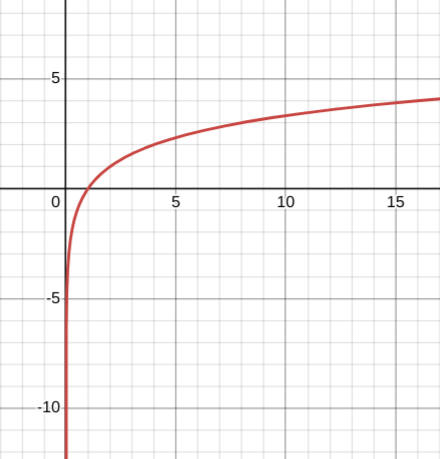
What graph is this?

y = log2(x)

Arithmetic Series Equation (+ or -)

Recursive formula?

an = a1 + d(n-1)

an = an-1 + d

Sum of a Finite Arithmetic Sequence

Sn = (a1 + an) x (n/2)

Geometric Sequence Equation (x or /)

Recursive Formula?

an = a1 x r^(n-1)

an = an-1 x r

Sum of a Finite Geometric Sequence?
Sum of an Infinite Geometric Series?

Sn = a1( (1 - r^n)/(1-r) )

S = a1 / (1-r)

nCr = ?

n! / (r! x (n-r)! )

nPr = ?

n! / (n-r)!

Equation for Distinguishable Permutations

n! / (n1! n2!…nk!)

sin =

cos =

tan =

csc =

sec =

cot =

y/h

x/h

y/x

h/y

h/x

x/y

cos(-θ) = ?

cos(θ)

sin(-θ) = ?

-sin(θ)