Comp Bio 4th test

What does structural biology primarily focus on exploring? Why study structure?

Structural biology studies the 3D shapes of biological macromolecules and how these shapes relate to function

Why? - Proteins and nucleic acids adopt specific shapes crucial for their biological roles

What does protein play key roles in as a the primary targets of most small-molecule drugs?

These proteins play key roles in signaling, metabolism, immune response, and other vital functions.

Modulating protein activity with small molecules allows us to influence biological pathways precisely

When are proteins good drug targets?

When it is causally linked to disease

• Not every protein is “druggable”. Target selection must be biologically and chemically justified

• Genomics, proteomics, and phenotypic screens help identify candidate targets

What it is the criteria for selecting a protein target? 

• Disease relevance: The protein plays a critical role in the disease mechanism

• Druggability: The target has a structure that allows it to bind with drug-like molecules

• Specificity: Targeting the protein minimizes effects on healthy cells, reducing side effects

What is the foundation of nearly every process in a living cell?

The specific, noncovalent binding of molecules

• Life operates through a complex network of molecular “conversations”. This process is called Molecular recognition

• These interactions are the basis for nearly all biological processes

• Our goal is to build a qualitative framework to describe the strength, or affinity, of these interactions using thermodynamics

What is a molecule’s final shape a dynamic balance of?

A molecule's final shape is a dynamic balance between two opposing forces

• The “molecular glue” aka potential energy

  • Attractive forces that pull parts of a molecule together

  • What it does: Lowers the system’s energy, creating a stable structure

What are the different non-covalent interactions that arise because of X?

All non-covalent interactions arise from the attraction between electron-rich (lump) and electron-poor (hole) regions of molecules

Electron-Rich Regions ("Lumps"):

• Areas with a surplus of electrons (negative potential)

Electron-Poor Regions ("Holes"):

• Areas with a deficit of electrons (positive potential).

How is a systems energy distributed?

The number of ways energy can be arranged in a system for a given macrostate is called its multiplicity (W)

How can we modulate a proteins functions?

We can modulate protein's function by binding small molecules to specific sites

• A protein’s activity can be altered by binding a small molecule—often called a ligand—to a functional site on its surface.

• This interaction can inhibit, activate, or subtly reshape the protein’s behavior.

• These small molecules act like “molecular switches” that control protein action without altering the underlying gene

Protein-ligand binding is a dynamic, reversible equilibrium

• The fundamental binding reaction is written as: P + L ⇋ P L

• This equation describes the equilibrium between unbound Protein (P) and Ligand (L) and the noncovalent Protein-Ligand complex (PL)

• Weak forces like ionic bonds, hydrogen bonds, and hydrophobic interactions hold the complex together. It is not a permanent, covalent bond.

• The complex is constantly forming and dissociating at equilibrium.

What does binding affinity and specificity determine? 

A molecule’s effectiveness as a modulator

• Not every small molecule that binds a protein is useful—effective modulation depends on how tightly and selectively it binds.

• High-affinity binding ensures that a drug is effective at low doses, while specificity minimizes off-target effects.

These properties can often be optimized through structure-based design and screening campaigns

High-throughput screening (HTS) allows testing of thousands of compounds against the target protein

• Library Preparation: Collection of diverse compounds

• Assay Development: Design of biological assays to measure compound activity against the target

• Screening: Compounds are tested in miniaturized assays

Data Analysis: Identification of "hits" that show desired activity

Molecular binding is complex, dynamic, physical event, why is it no just a lock and key model?

• Atoms in the protein and ligand are constantly vibrating and moving.

• Solvent: Thousands of water molecules form a hydration shell that must be displaced.

• Flexibility: The protein itself may change shape ("induced fit") to accommodate the ligand.

• Forces: All interactions are ultimately governed by quantum mechanics

Why is a perfect physical simulation is computationally impossible?

Problem 1: Accuracy. A true quantum mechanical calculation is too slow for large systems like proteins.

Problem 2: Scale. Simulating one compound for a few microseconds could take weeks on a supercomputer.

• We need to screen billions of compounds, not just one

What is the simplification called when translating the complex physical problem to a simple mathematical problem

It is called abstraction.

We develop a mathematical model—an objective function—that boils down the complex physical state into a single number.

This "score" represents our simplified definition of "goodness."

Is this a "good" 3D pose?

Is this a "good" ligand?

The entire goal is to create a function that is both:

1. Fast enough to run millions of times.

2. Accurate enough to tell a good binder from a bad one.

An objective function defines the problem.

Optimization solves it.

The objective function is what that calculates a conformational energy? 

Molecular Mechanics (MM) provides the equation for our objective function. It models molecules using classical physics:

Atoms = "balls" (particles)

Bonds = "springs"

The "score" it calculates is the conformational energy: the potential energy of a specific molecular shape, or pose.

MM conformational energy is a relative score, not an absolute truth, why is that? 

The score from a force field is not an experimentally measurable energy

Its purpose is not absolute, but relative.

The goal is to accurately determine if Pose A is "better" (has a lower energy score) than Pose B.

Is an approximation

What is optimization?

Optimization is the computational search for the best score (e.g., the minimum energy) by changing the inputs (e.g., the ligand's pose).

What equation/model is used that takes a 3D pose and returns a score? 

This model is called a Molecular Mechanics (MM) Force Field.

It is the specific set of equations and parameters (constants) used to calculate the potential energy of a molecule in a given 3D arrangement, or conformation.

This equation is our objective function:

Energy = f(Pose)

E total = E bonded + E non-bonded

E bonded (internal energy)

• Energy inside the molecules (e.g. the ligand)

• This is the energy “cost” for the ligand to change its shape

• Calculated by bond stretching, angle bending, bond twisting

E non-bonded (interaction energy)

• The energy between separate molecules

• This is what we use to define a “good” pose

• Calculated using:

  • Van der waals

  • Electrostatics 

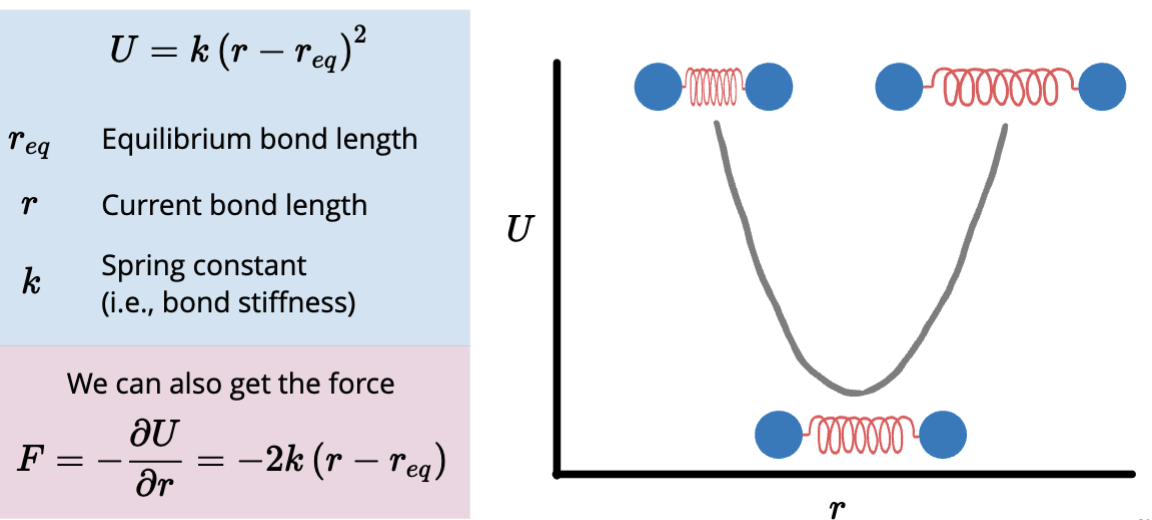
Chemical bonds behave like springs, what is the equation that represents the approximate bond vibrations as harmonic oscillators?

Spring constants are therefore determined by bond order and atom types.

Bond angles behave like harmonic oscillators, having separate spring constants for bond angles.

• V = k(0i - 0eq)²

Whats the difference between dihedrals vs Bonds and angles?

• Bonds and Angles: Govern local geometry (bond lengths and bond angles) using quadratic (harmonic) potentials that favor specific distances and angles.

• Dihedrals: Govern torsional or rotational flexibility around bonds, typically using periodic or multi-well potentials to allow for multiple stable conformations.

How do we model dihedral potentials?

Well they must capture arbitrary functions with rotational symmetry, so we use custom fourier series

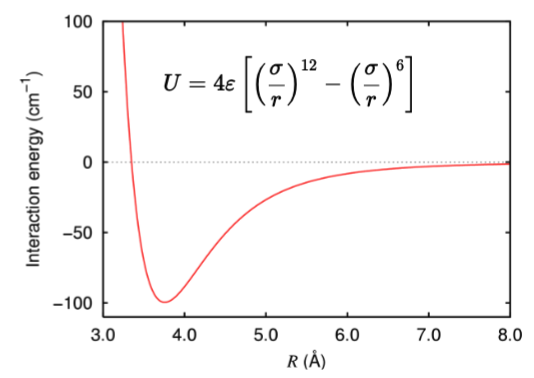
What does van der Waals (vdw) forces describe in atoms?

Atomic “stickiness” and “clashing” 

This is an intermolecular force between atoms not directly bonded.

Has two parts that depend on the distance r:

• Strong Repulsion (r^-12 term): At very short distances, the energy explodes (highly positive)

  • “Clash” as two atoms cannot be in the same place 

• Weak Attraction (r^-6 term): At a "sweet spot" distance, there is a small negative (favorable) energy.

  • “Stickiness” A weak induced dipole attraction that helps hold the molecules together.

What does Electrostatics interactions drive?

Charged and Polar molecule behavior.

Electrostatic forces decay as 1/r, making them significant over longer distances compared to van der Waals forces

vdW and Electrostatics work together to

define a "good" binding pose, compare the two.

van der Waals (Lennard-Jones):

• Governs shape complementarity.

• Answers: "Does it fit?"

• Provides a strong penalty for clashing.

• Provides a weak reward for close packing.

Electrostatics (Coulomb's Law):

• Governs chemical complementarity.

• Answers: "Is it a chemical match?"

• Provides a strong reward for matching charges (e.g., H-bonds).

• Provides a strong penalty for mismatched charges

These two forces are the core of our binding energy calculation.

While vdW and Electrostatics are powerful, they are incomplete and are missing the two biggest drivers of binding:

Solvation (The Hydrophobic Effect):

• Binding is often driven by entropy, not just energy.

• "Ordered" water in the binding site is "freed" when the ligand binds. This release of "caged" water is a massive thermodynamic "win" that our simple equation does not capture.

The Dielectric Constant (Screening):

• Our Coulomb's Law (magnets) works in a vacuum.

• Water is a continuum that dampens or "screens" these forces.

• This completely changes the strength of our "magnets."

What is scoring function?

"Scoring function" is the specific name for

the objective function in molecular docking

What are docking’s three primary goals?

Pose Prediction (Ranking Poses): Is this the correct pose?

• Out of 1,000 possible poses, you just have to pick the one correct answer

• Finds optimal molecular configuration

Affinity Prediction (Scoring): How tightly does this molecule bind? HOLY GRAIL but very difficult

• You must provide a precise, quantitative, numerical answer (the Ki) that matches reality.

• Aims to predict the actual, experimental binding strength

Virtual Screening (Ranking Molecules): Is this an active or inactive molecule? aims to separate "hits" from "decoys" in a large database

• You don't need the single best answer at rank #1. You need the first page of results to be highly relevant and useful.

Why is “physics in a vacuum” model flawed but provides a good starting point?

Our simple Molecular Mechanics (MM) force field is good at Pose Prediction (Goal 1).

It is bad at Affinity prediction (goal 2).

• Completely ignores the two most dominant thermodynamic forces in biology:

1. Solvation/The Hydrophobic Effect (driven by entropy).

2. Solvent Screening (the high dielectric of water).

The Solution: We must create new scoring functions. These functions are different "philosophies" for approximating these complex, missing terms

We can group scoring function into four major families or philosophies, what are they?

• The "Purist" (Physics-Based): Tries to model "pure" physics.

  • Use data to train our model using a training set, real data to fix the pure physics model

• The "Pragmatist" (Empirical): Uses real data to "fix" the physics model.

  • Fits it to real data

• The "Apprentice" (Machine-Learning): Uses powerful algorithms to find complex patterns in data.

How is The "Pragmatist" (Empirical) built?

The equation is a weighted sum, typically found using linear regression

1. Get a "training set" of complexes with known Ki values.

2. Calculate all the energy terms (vdW, H-bonds, etc.) for all of them.

3. Use a computer to solve for the weights (w_1, w_2, w_3...) that make the Score best correlate with the real Ki values

Pros:

• Once weights are found, it's just a simple sum.

• Explicitly designed to be good at Affinity Prediction.

Cons:

• It's "trained" on a specific set of proteins. It may fail badly on a new system that is very different (e.g., it may not be "transferable")

How is The "Modern Apprentice" (ML) built?

1. Features: Generate hundreds of "descriptors" (features) for each complex.

2. Model: Use a complex, non-linear algorithm like a Random Forest (RF), Support Vector Machine (SVM), or Deep Neural Network (DNN).

3. Train: Feed the model massive amounts of data (e.g., 10,000 "actives" and 1,000,000 "decoys") and "train" it to distinguish them

Pros:

• Highly Accurate: Can be the best-in-class for screening by finding patterns no human or simple equation could

Cons:

• "Black Box": Can be un-interpretable. It might tell you "this is a hit!" but not why.

• Data Hungry: Needs massive amounts of high quality training data.

• Overfitting: Can "memorize" its training data and fail when it sees a new type of molecule

How do we build (or “fit”) an Empirical or Machine-learning scoring function?

The Solution: We use another objective function!

• This new objective function's goal is not to score a pose, but to score the entire scoring function itself.

• Its goal: To minimize the error

We do this my optimizing an “error function”

This entire process is called supervised learning.

• Step 1: Get Data (Training Set). Gather 100s of complexes with known, experimental binding affinities (e.g., Ki).

• Step 2: Make a Guess. Start with random weights (w1=0.1, w2=0.5...).

• Step 3: Predict & Measure Error. Use our function to "predict" the affinity for all 100 complexes. We quantify this "wrongness" with an error function (or "loss function").

• Step 4: Optimize!

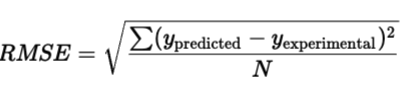
  • The RMSE is our new objective function.

  • The weights ($w_1, w_2...$) are our new decision variables 

  • We use an optimization algorithm to find the set

We validate our model on a “test set”: data it has never seen before, how is this done and how do we read the results?

This is the most important part of building a new model.

• Training Set: The data we show the model. We use this to fit the weights (i.e., minimize the RMSE).

• Test Set (or Validation Set): The "final exam." This is a separate, "held-out" set of data that the model never sees during its training.

The Real Test of a Model:

1. You train your model on the Training Set.

2. You then use this final, frozen model to make predictions on the Test Set.

How to Read the Results:

• GOOD Model (Generalization): Low error on both the training set and the test set. (It learned the "rules"!)

• BAD Model (Overfitting): Very low error on the training set, but a high error on the test set. (It "memorized"!)