Electromagnetic Spectrum

investigate Maxwell’s contribution to the classical theory of electromagnetism (summary)

Maxwell’s theory regarding light

• An oscillating charge produces changing electric and magnetic fields that produce a self-propagating wave that traves at 3x108m/s

• Light is an EM wave

• EM waves are transverse

His contributions

• His equations

  • Unified concepts of electricity and magnetism under one phenomena of electromagnetism

• His thought experiment on how to make EM waves

  • Discovered how EM waves were formed + its self-propagating nature

  • From this nature, he determined that EM waves were transverse  since to make an EM wave, a charge is oscillating up and down, but the direction that the wave is travelling/propagating is perpendicular

• Derived the velocity of EM waves using his equations  similar to the speed of light as calculated by other experiment

  • light was an EM wave

  • Found that there is a spectrum of EM waves, since if we change the frequency infinitely to create different waves and light is a category of this spectrum

All of his work was confirmed by Hertz later on through his experiments

Contribution 1: Maxwell’s equations

• A set of four equations that describe the behaviour of electric and magnetic fields and how they relate to each other

• Published in 1865

Describes	Law	Meaning
Nature of static fields	Gauss’ Law	States that static electric charges have an electric field Note: static charges only affect other charges
	Gauss’ law for magnetism	Magnetic fields do not exist as monopoles (must be north and south poles, not only one), thus the field lines form closed loops Note: Static magnets only affect other magnets, not charges
Interactions between fields (inseparable)	Faraday’s law	That a change in magnetic field gives rise to an electric field change in flux is created by a change in magnetic field this induces an EMF which causes electric lines to flow in that conductor allows for an induced current to occur, since electric fields causes a force to be experienced on a charge Note: Moving magnets will affect a charge/induce a current in a conductor (e.g. AC induction motor)
	Ampere’s Law	Current gives rise to a magnetic field A changing electric field causes a changing magnetic field → Proposed by Maxwell to seek symmetry in Faraday’s and Ampere’s law Note: Moving charges creates a magnetic field (e.g. current in a wire)

Result / impact of Contribution 1: Maxwell’s equations

His equations transformed the way that physicist understood light and EM waves, since previously electricity and magnetism were studied separately

Through Faraday’s Law and his modification to Ampere’s Law, Maxwell unified these two concepts under one phenomenon called electromagnetism, which describes the interaction between charged particles

• The symmetry between Faraday and Amperes law shows that magnetic fields and electric fields are intrinsically linked:

  • Oscillating electric fields would produce magnetic fields

  • Oscillating magnetic fields would produce electric fields

  • A moving electric charge would thus produce a magnetic field due to the presence of its intrinsic electric field.

These equations unifying electromagnetism led him to other discoveries

• Finding the equation of the speed of EM waves (thus predicting that light was EM radiation)

• The self-propagating nature of EM waves

• EM waves are transverse wave

Contribution 2: Maxwell predicted the existence of EM waves by describing their production and propagation

From the wave equation and by conducting a thought experiment, Maxwell used the laws in his equations to determine how light was able to travel without a medium:

1. If a single electric charge accelerates and decelerates (moves up and down), it creates an electric field that changes with time

2. According to Ampere’s law, this creates a perpendicular magnetic field

   1. Which is why the right-hand palm rule has current/charge movement, B field and force at right angles (Fingers = B field, thumb = conventional current / E field, palm = force / direction of propagation)

3. Due to the movement of the charge, the magnetic field is also changing with time

4. According to Faraday’s Law, the moving magnetic field would then create an electric field

5. Since this new electric field is also changing overtime, they would create new magnetic field lines

6. This continues in a cycle, creating more changing electric and magnetic fields

7. Thus, a self-propagating wave is created

   1. No medium required for light to travel, since the moving charge continuously makes changing electric and magnetic fields that then in turn create the other type of field.

This also correctly predicted that a passing EM wave causes charged particles to oscillate → like how a water wave causes a duck in a pond to oscillate

Result of Maxwell Contribution 2:

Proposed electromagnetic waves consisted of a self-sustaining mutual generation of electric and magnetic fields that propagate at the speed of light

→ light’s self-propagating nature (and all other EM waves)

• Self-propagating – can travel through vacuum / does not need a physical medium required to travel or propagate

• Revealed how EM waves could travel without a medium, and thus could travel through space  however at this time people still believed that there were particles in space called the aether

This established that EM waves are transverse

• In this experiment, the fact that the charge is oscillating in one direction (e.g. up and down), but the changing electric and magnetic fields are being propagated outwards, shows the direction of propagation and oscillation are perpendicular

Contribution 3: Maxwell’s Wave Equation

Maxwell combined his equations describing electromagnetism to produce another equation called the wave equation, which calculates the speed of EM waves

• Extended on the existing wave equation: v=fλ → derived from v=s/t

Involves the constants:

• the permeability of free space (resistance against the formation of a B field in vacuum)

• the permittivity of free space (resistance against the formation of an E field in vacuum)

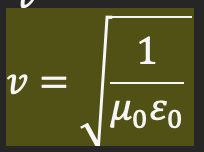
Result of Maxwell Contribution 3

The answer to Maxwell’s wave equation indicated that light must be an EM wave

• The speed of light waves was known to be ≈3×10^8 through experimental measure

• The discovery that EM waves travelled at around this speed suggests that light is an EM wave

Indicated that there was an electromagnetic spectrum  how fast you oscillate the charge changes the frequency, which impacts the type of radiation generated

• Light was known to be a wave (has frequency and wavelength)

• Visible light was known to disperse into different colours after (double) refraction

• Other types of EM radiation like UV and infrared had already been discovered

• By changing the frequency, different types of EM waves can be created

• Continuous spectrum → indiscrete frequencies

The Production of EM Waves

• An AC voltage applied to the wires of an antenna forces electric charge in the antenna to oscillate

  • The frequency of this AC voltage is the same as the E field

• This accelerates charge particles → is a source of EM waves

• Fundamental mechanism to make EM waves: Acceleration of charges

  • Accelerating charges produces a changing current

  • According to Ampere’s law, this produces a changing magnetic field

  • According to Faraday’s law, this produces a changing electric field

Heinrich Hertz’s Experiments Overview

All of Maxwell’s discoveries were reinforced by Heinrich Hertz’s Experiments in 1886

• He made radio waves, which had all the properties of a waves

  • Demonstrated they could be reflected, interfere and be polarised

  • It travelled at the same speed predicted by maxwell’s equation

  • These waves had similar properties to light, but only differed in frequency and length

• Lead to the conclusion that

  • Visible light is an EM wave that obeys Maxwell’s equations

  • Visible light is a part of a broader spectrum of EM radiation

Description of Heinrich Hertz’s Experiment

1. An emitter antenna was connected to the power supply

2. When the power was turned on, sparks form in the gap at the centre of the antenna

   1. Sparks are formed when electrons jump from one side of the gap to the other

   2. Indicates that current was flowing

3. This antenna generated radio waves

   1. Since the electrons were being accelerated through the gap = produced changing E and B fields = EM waves

4. Hertz stood at a distance away holding a receiver antenna with a gap in it

5. The receiver antenna detected the oscillating electric fields of the radio waves

   1. These electric fields caused the electrons in the receiver to accelerate to produce a changing electric current that the same frequency as the emitter

   2. Sparks across the receiver gap indicated there was a current flowing in the antenna, despite it not being connected to power → indicates energy was being transferred

Hertz calculating the speed of radiowaves

Set up experiment as described

6. Hertz reflected the generated waves off a metal sheet

   1. Shows that radio waves can be reflected and interfere → two properties of waves

7. The incident and reflected rays interfere to create a standing wave

8. Hertz measured the wavelength by finding the distance between antinodes

   1. He moved his receiver coil along the wave, and a spark was produced where there was an anti-node

   2. Anti-node = oscillating = there is a change in electric field = sparking

   3. Node = no oscillation = no sparking

9. From the distance between antinodes is half the distance of a wavelength

10. Using the wave equation, v=fλ, he calculated the speed of the wave to be 3x10^8m/s → matching Maxwell’s prediction

    1. Hertz already knew the frequency of the wave → He used AC voltage, which has an identical frequency to the oscillating E field it creates

    2. When he changed the frequency (and thus wavelength) of the waves, he obtained the same speed value for all the waves he created

Hertz polarisation of radiowaves

Through polarising radio waves by changing the orientation of the receiver, he proved they were transverse  like light

1. When he rotated the gap’s orientation, the spark’s intensity would increase and decrease

   1. By holding his receiver’s gap parallel to the emitter gap, there was the most sparking

   2. If the receiver’s gap was perpendicular to the emitter’s gap, there was no spark induced

2. Shows that the emitter was producing polarised waves

   1. Electric field oscillates along one axis, waves are polarised in this direction

   2. The receiver can only detect wave with the electric field oscillating across the spark gap → since this is the only way that charges can be accelerated across the gap

Historical questions about the speed of light

People always wondered whether light travelled at a finite or infinite speed

• If it was finite, it could be experimentally measured

• People thought it might be infinite because it travels so fast, and in early history, there was no technology to measure it

• Overtime, people used previous experimental results to further accurately measure light’s speed

Historical measurements of the speed of light: Ole Romer

By observing the motion of Io (one of Jupiter’s moons)

• Io would temporarily disappear from view on earth when it was eclipsed by Jupiter

• Eclipse occurred quite regularly (every 42.5 hours)

• Rømer observed that during specific times of the year, the eclipse times changed

  • When the earth is moving towards Jupiter, light has a shorter distance to travel →the eclipse appears to occur earlier

  • When earth is moving away from Jupiter, light has a further distance to travel → the eclipse appears to occur later

• He concluded that the time between eclipses appeared to change since light was travelling at a finite speed

• Estimated that light would take 22 minutes to travel the distance of Earth’s orbit around the Sun

Historical measurements of the speed of light: Hippolyte Fizeau

1. He reflected a beam of light on a mirror 8km away, so that when it returned on to a target, he replaced a rotating cogwheel in the path of light

2. Light must pass through the gap between the cogs to reach the mirror, so light could be seen from behind the cog

3. As the light travels to the mirror, the wheel continues to rotate

   1. If it rotates half a distance between the cogs in that time = the returning light is completely blocked → cannot be seen

   2. If it rotates a full distance = the returning light will travel through the adjacent gap → can be seen

4. He increased the rotational speed of the wheel until light was blocked

5. The calculated the time it took for the wheel to move half a space along from the rotational speed of the cog wheel, to give the time of flight

6. He measured the speed to be around 3.1x108m/s:

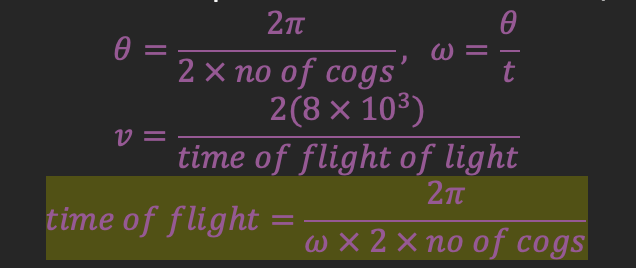
Hippolyte Fizeau - Impacts of specific rotational speeds of the cogwheel

Light’s relationship with distance and time

The current value of the speed of light was defined in 1983

• Meant that the metre had to be redefined in terms of the speed of light

• Metre - The distance light travels in 1/299792458 seconds

• This new definition is used by astronomers today, since space is so large and in SI units results in very big and impractical numbers

e.g. 1 light year = the distance travelled by light in one earth year

The Bohr Model of the Atom

• Electrons orbit the nucleus in stable energy levels (aka correct version of electron shells)

• There are multiple energy levels in an atom

  • The further away an orbit is from the nucleus, the greater the associated energy level it has.

  • Atomic electrons naturally occupy the lowest energy state (the ground state)

  • Higher energy states are called excited states

• When electrons absorb a specific amount of energy (e=hf), they move to a higher energy level → orbit further away from the nucleus

• Electrons don’t remain in their excited state permanently → they naturally they want to return to a lower, more stable energy level by releasing electromagnetic energy (e=hf)

Types of Spectra

• Each element has a different emission/absorption spectrum

• There are usually more than one absorption/emission line

  • ground state electrons can be excited to different energy levels by absorbing different amounts of energy (and release that energy back out as EMR)

Continuous spectrum – no spectral lines since all frequencies of radiation is emitted

• Only emitted by the cores of black bodies and incandescent lightbulbs

Emission spectrum – coloured/banded lines are all the frequencies that are being given off by electrons

• Hot gas (needs to have energy to emit) → diffraction grating/spectrometer →emission spectrum is made

Absorption spectrum – the black bands are the frequencies that are not being absorbed (aka they are being emitted)

• Continuous wavelength source provided → Cold hydrogen has (needs to absorb the energy from the source) → absorption spectrum is made

Balmer Series

Hydrogen Spectral Lines

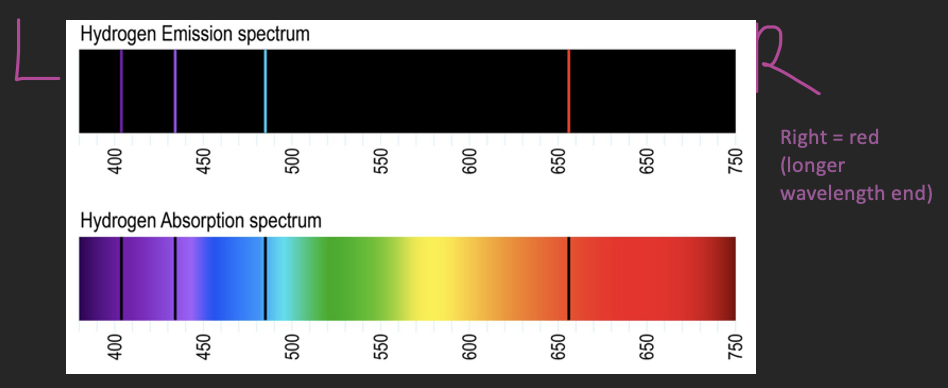
How to generate spectra for elements using a discharge tube

1. Power source provides potential difference between the cathode (- side) and the anode (+ side) of the discharge tube

2. Electric field lines form

3. When voltage is high enough, electrons from metal on cathode jump to the anode

4. When they move through the gas, they bump into the electrons of the gas’s atoms

5. The moving electrons transfer their energy into the electrons in the atom

6. These atom electrons absorb this energy and enter an excited state which allows them to move up discrete energy levels (E=hf)

7. The atom electrons then transition back down energy levels, releasing energy as they move down each one → move down to reach a more stable form

8. This energy is given off as photons of light

9. The spectral lines we see using a spectrometer show the most common discrete frequency that the atom electrons emit when they undergo energy transitions

   1. More intense spectral line (brighter) = more frequencies of photons being emitted due to more electrons undergoing that energy transition

10. The colour we see overall is a mix of the most common frequencies of photons emitted

Spectrum of Reflected Sunlight

• The core of the sun produces a continuous spectrum due to nuclear fusion

• This energy is released as photons

• The electrons in the outer layer of gas in the sun absorbs these photons, enter an excited state and then relax back to ground level to re-emit the energy → emits as certain frequencies of EMR

• We do not receive a continuous spectrum from earth due to this process

• We can study the absorption and emission spectral lines to find the information about the sun (see: Viewing Stellar Spectra to Study Stars)

• Gas in the Earth’s atmosphere cause more absorption lines

  • Blue light (higher energy) is absorbed by atmosphere to excite the electrons in the air

  • Carbon dioxide absorbs infrared radiation and longer wavelengths of visible light

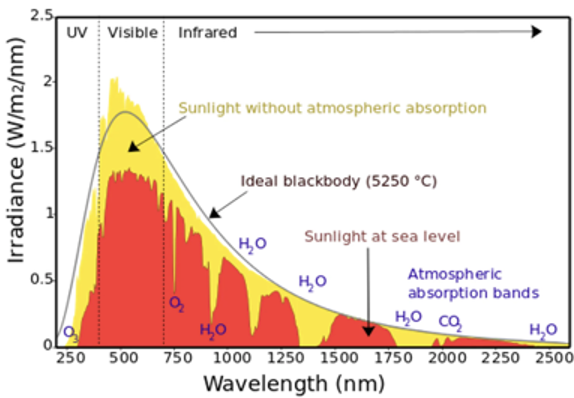
Spectrum of Incandescent Lamps and Filaments

• Electric current passes through a high resistance conductor until it reaches melting point

• Collisions between the electrons and the atom in the conductor produces heat and light

• The spectrum generated continuous  emits more red-light photons (warmer glow)

  • Not a result of electronic excitation

  • The filament emits light at all visible wavelengths when heated to high temperatures

  • Inefficient because most of the wavelengths emitted are in the red/infrared range, not visible light

Using spectra of elements to identify elements

• Each element has a different atomic structure

• Means each energy level for the electrons in the atom are different

• These different energy levels mean that different frequencies of photons are emitted → we can see different colours

• If we have a compound, we can match up the spectral lines of that compound the known spectral lines of elements to see its elemental composition

how the spectra of stars can provide information on surface temperature

Surface Temperature – the temperature of the outer layer of stars

• The spectra of stars consist of a wide range of wavelengths

• Each wavelength of radiation has a different intensity

• Peak wavelength (λ_max) = the highest intensity wavelength

• We use Wein’s displacement law to compare surface temperature between stars:

  • Shorter λ_max = higher surface temperature (hotter)

    • ↓λ_max= ↑ frequency = light emitted is in blue part of the spectrum = hotter

  • Higher λ_max = lower surface temperature (cooler)

    • ↑λ_max= ↓ frequency = light emitted is in red part of the spectrum = cooler

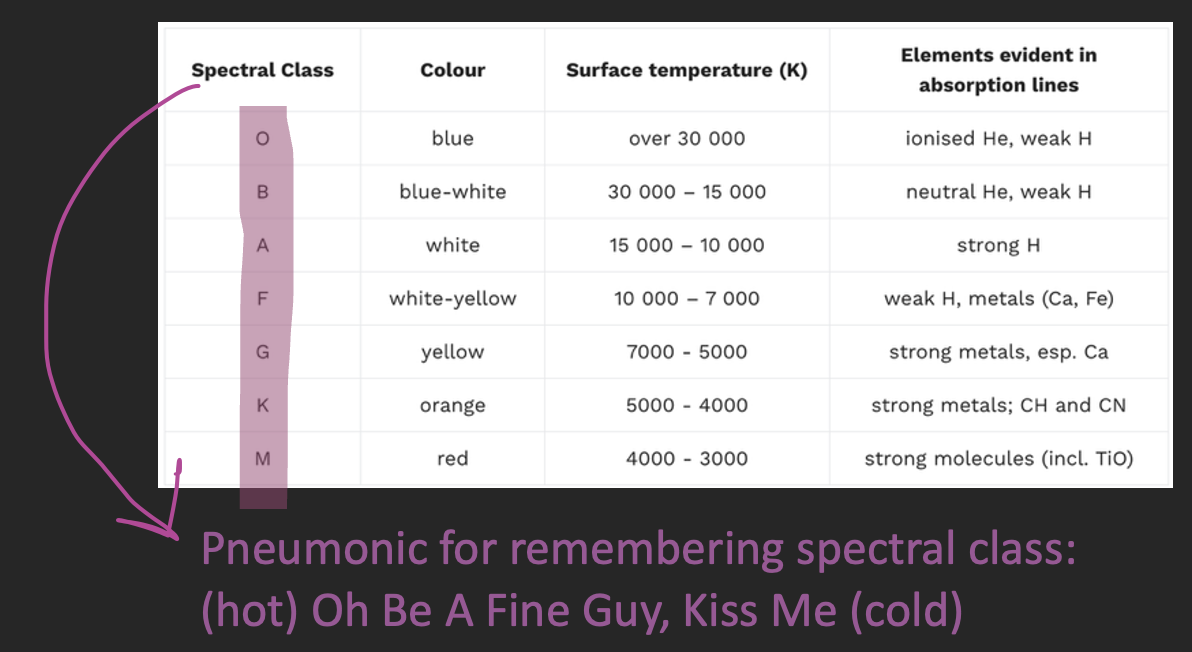
how the spectra of stars can provide information on chemical composition

• Stellar absorption lines are caused by atoms in outer gaseous layers of stars

  • When light is emitted by stars, some of is energy is absorbed by the outer layer

  • This occurs when the energy matches exactly the excitation energy of electrons in the ground state of these elements (e=hf)

  • The absorption spectral lines represent the energy that has been absorbed by these electrons

• Stars are made of many different elements ∴ absorption spectra of every star is different

• We compare the relative position and number of absorption lines from the star to the spectrum of elements on Earth to identify the exact elemental composition

• If the star has compounds (two/more elements bonded), there are more energy levels possible for electrons → energy levels are less well defined → broader and more blurred spectra

how the spectra of stars can provide information on density

Density – how tightly compact the atoms are together

• Density / pressure = impacts breadth of spectral lines

  • Greater density = broader/blurrier absorption lines

  • Lower density = thinner absorption lines

Higher density surface of star

= Increased gas pressure

= More rapid collision between atoms

= More exchanges of energy

= More variety of energy levels  some electrons gain some energy from collisions, but some lose energy

= Creates wings on the spectrum that extend out farther from the centre of the line, but the intensity stays the same

= Means that the lines are not as clear/defined and smooth

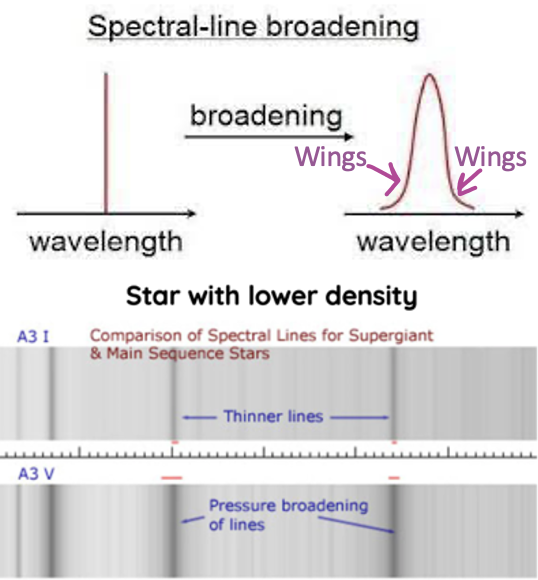
how the spectra of stars can provide information on rotational and translational velocity

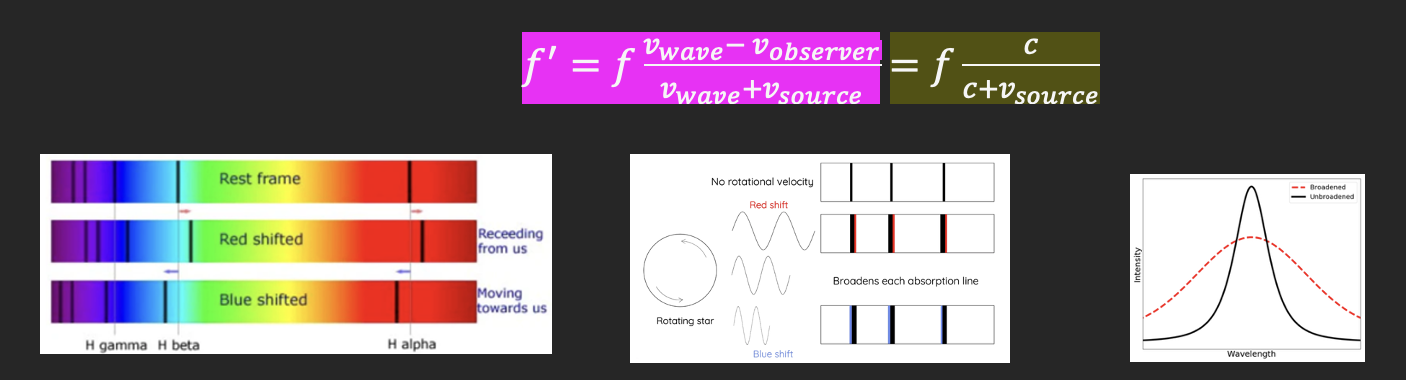
The Doppler Effect - when the wavelength of a wave is influenced by the wave’s relatively velocity to the observer.

Translational velocity

• Blueshift – when all waves emitted shift to a lower wavelength due to the star moving towards the observer

  • If the wave source (star) is moving towards the observer = shorter wavelength of resultant wave = blueshift

• Redshift – when all waves emitted shift to a higher wavelength due to the star moving away from the observer

  • If the wave source (star) is moving away from the observer = longer wavelength of resultant wave = redshift

Rotational velocity

• Wave emitted from the side of a star that is rotating towards us has shorter wavelength (blue-shifted)

• Wave emitted from the side of a star that is rotating away from us has longer wavelength (red-shifted)

• Wave emitted from the ‘middle’ of a star (no relative rotation to an observer on Earth) has no change in wavelength (no change)

= Doppler broadening

• The rotational velocity of the star means that some wavelengths are redshifted and some are blue shifted

• Different velocities of the emitting/absorbing particles result in different Doppler shifts

• This allows for a greater variety of frequencies for the emission spectral line

• Since the intensity/energy of the light (area under the graph) remains the same, when emission line becomes wider, its peak become less high

Describe Hertz’s observations relating to the photoelectric effect

Discovered the Hertz Effect:

• His transmitter coil could generate UV light and radiowaves

• He noticed that his receiver coil sparked brighter when UV and radiowaves arrived

• When he blocked out the UV using quartz, the spark in the receiver coil was smaller, because only radiowaves could travel through the quartz and be received by the receiver coil.

• This suggested that UV was also responsible for an electrical response in the receiver, connecting the concept of light to electricity

  • this is consistent with the photoelectric effect (since high frequency light can cause the emission of electrons and generate a current)