M6 MacLean- Population Genetics of Adaptation I + II

what are the assumptions in the hardy-weinberg theorem and what does it state?

assumptions:

• there is an infinite population size

• mating is random

• the genes of interest have no impact on fitness/do not have differences in viability

the hardy-weinberg theorem states that allele and genotype frequencies in a population will remain constant from generation to generation in the absence of other evolutionary influences eg. mutations, selection, or genetic drift

P² + 2PQ + Q² = 1

P + Q = 1

how can the hardy-weinberg theorem be adapted to account for selection?

fitness (W) can be calculated- the relative reproductive rate of an individual with a given genotype (how likely the allele is to be inherited)

this is dependent on:

• the selection coefficient (s)- whether the allele is more beneficial (positive coefficient) or more deleterious (negative coefficient) than Q

• the dominance (h)- dominant = 1, recessive = 0

fitness is measured relative to Q, so Q = 1:

• the fitness of P in P homozygous individuals (P²) is 1+s

• the fitness of P in heterozygous individuals (2PQ) is 1+hs (accounts for whether it is dominant or recessive)

• the fitness of P in Q homozygous individuals (Q²) is 0

if you add the fitnesses for the P allele and the Q allele (1), you get the average fitness (W) = P²(1+s) + 2PQ (1+hs) + Q²(1)

the frequency of the P allele in the next generation is P²(1+s)/W + PQ(1+hs)/W

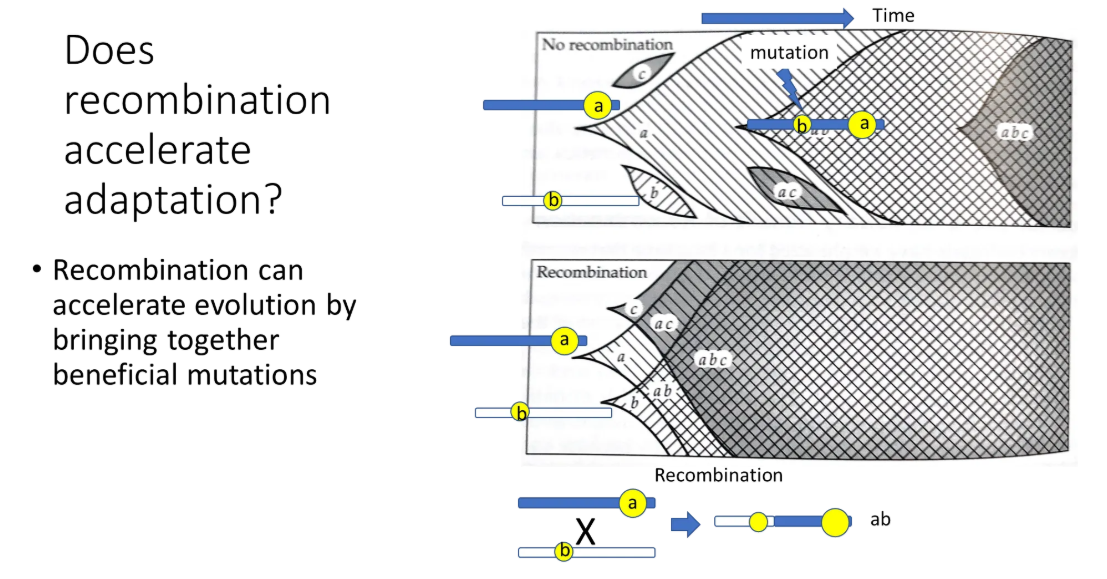
what is the graph of a beneficial allele frequency when it is introduced to a new population?

• recessive beneficial alleles take longer to fix in a population because they can only show a beneficial effect when homozygous, which is rare at first

• the frequency slowly increases at first, until some organisms are homozygous, where it causes a ‘selective sweep’ because that allele will then be greatly selected for

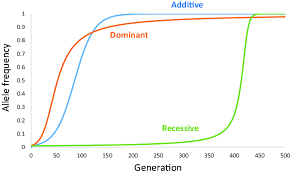
how can the hardy-weinberg theorem be adapted for an island model of structured populations?

the allele frequency in the next generation (on one island) is dependent on the migration rate (m)- the probability that the allele arrives on the island by migration

the frequency in the next generation (P₂) = P₁(1-m) + P* (m)

where P* = the average allele frequency on other islands

(the 1-m is because if there is migration of the allele onto the island, there is also migration of the allele off the island)

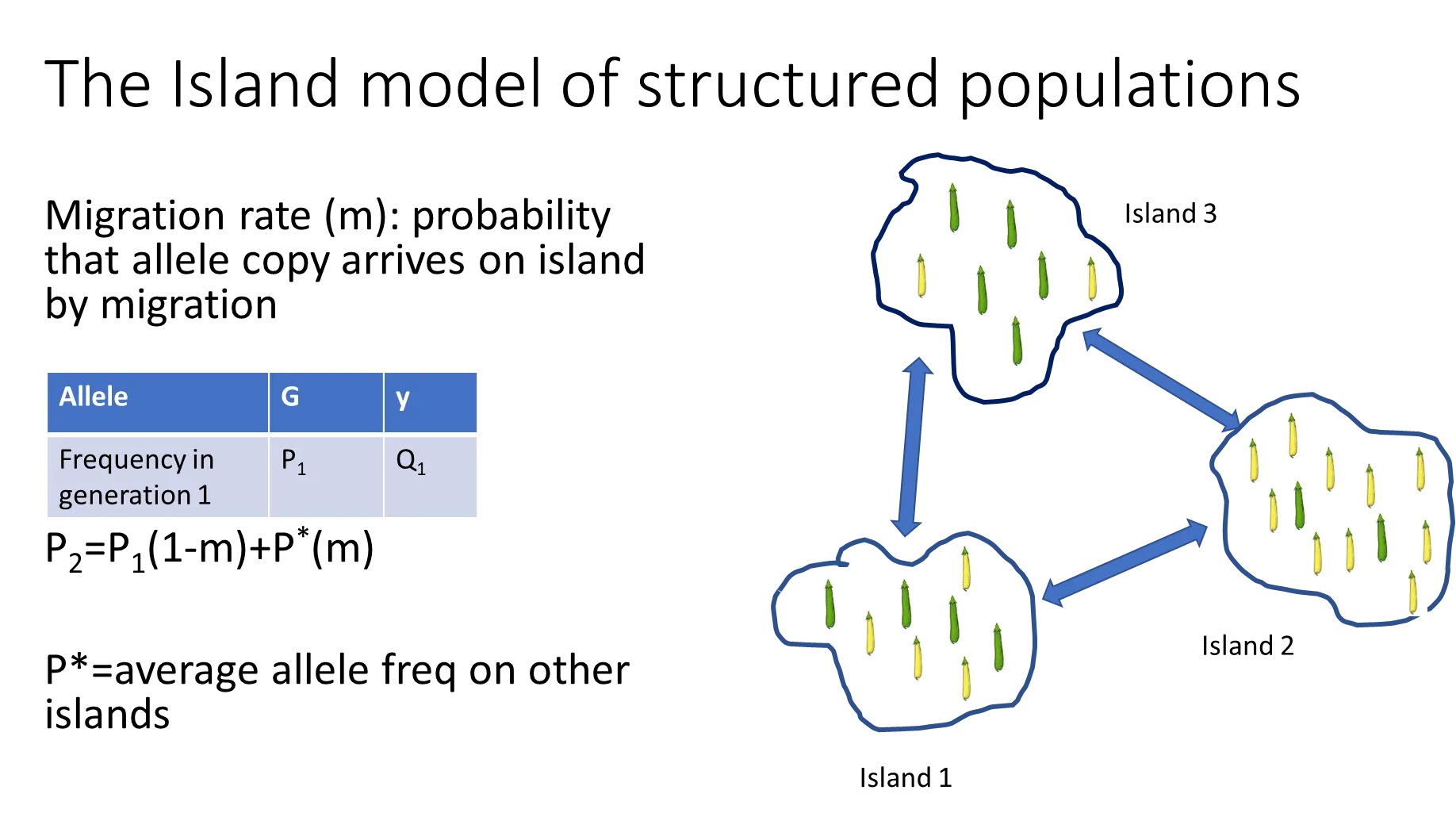
how does migration affect allele frequencies?

• if there is gene flow between populations, they will all eventually reach an average allele frequency

• the number of generations that this takes to occur is dependent on the rate of migration

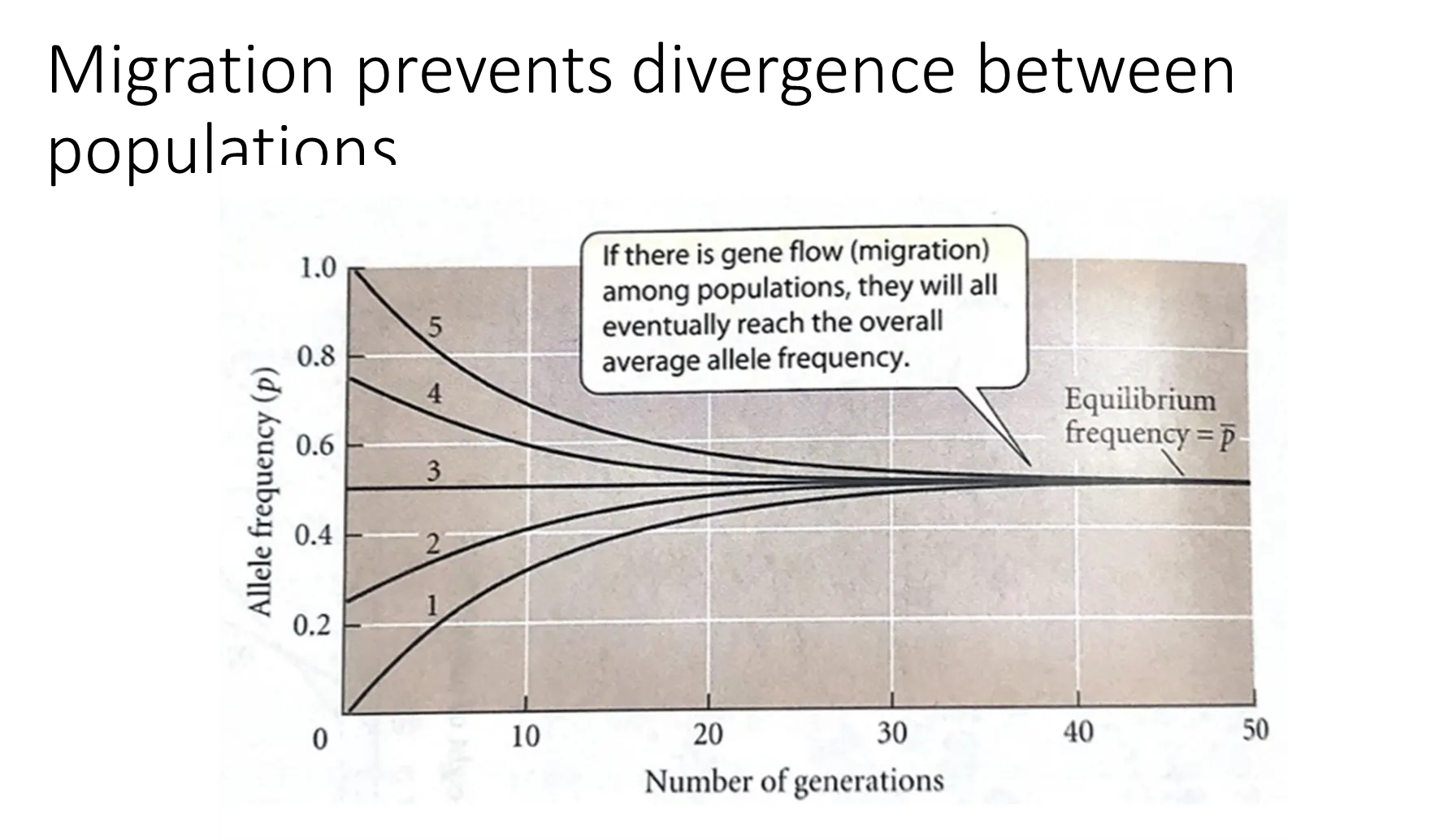
how does recombination affect adaptation?

• recombination accelerates adaptation and evolution by bringing together beneficial mutations

• without recombination (in a haploid population), two beneficial alleles would have to compete with each other, as they could never be inherited together

• in the top diagram, without recombination, b and c are outcompeted by a, and ac is outcompeted by ab

• in the bottom diagram, with recombination, evolution happens much faster because the beneficial mutations can combine

• sexual reproduction creates much greater genetic diversity through recombination