ACT MATH
0.0(0)
0.0(0)
Card Sorting
1/246
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
247 Terms
1
New cards
Area of a Triangle
A \= (1/2)(b)(h)
2
New cards
Area of a Circle
The formula to find the area of a circle is `A = πr^2`, where `A` is the area and `r` is the radius of the circle.
3
New cards
Circumference of Circle
The formula for the circumference of a circle is `2πr`, where `r` is the radius of the circle.
4
New cards
Perimeter of a Square
P \= 4(s)
5
New cards
Area of a Square
The area of a square is calculated by multiplying the length of one of its sides by itself. In mathematical notation, it can be represented as A = s^2, where A is the area and s is the length of one side of the square.
6
New cards
Area of a Trapazoid
a and b are the two bases
7
New cards
Area of a Rectangle
A \= (l)(w)
8
New cards
Perimeter of a Rectangle
The perimeter of a rectangle is equal to the sum of all its sides. If the length and width of the rectangle are denoted by `l` and `w` respectively, then the perimeter `P` can be calculated as:
`P = 2l + 2w`
Therefore, the formula for the perimeter of a rectangle is `P = 2l + 2w`.
`P = 2l + 2w`
Therefore, the formula for the perimeter of a rectangle is `P = 2l + 2w`.
9
New cards
Properties of a Rectangle
-4 right angles; -Diagonals bisect each other and are congruent; -Opposite sides are equal
10
New cards
Similar Triangles
corresponding angles are equal, corresponding sides are proportionate
11
New cards
Pythagorean Theorem
a^2 + b^2 = c^2
12
New cards
Sine Ratio
SOH
Opposite leg/ hypotenuse
Opposite leg/ hypotenuse
13
New cards
Cosine Ratio
CAH
adjacent leg/ hypotenuse
adjacent leg/ hypotenuse
14
New cards
Tangent Ratio
TOA
opposite leg/ adjacent leg
opposite leg/ adjacent leg
15
New cards
Distance Formula
The distance formula is a mathematical formula used to calculate the distance between two points in a coordinate plane. It is given by:
`d = sqrt((x2 - x1)^2 + (y2 - y1)^2)`
where `d` is the distance between the two points `(x1, y1)` and `(x2, y2)`.
`d = sqrt((x2 - x1)^2 + (y2 - y1)^2)`
where `d` is the distance between the two points `(x1, y1)` and `(x2, y2)`.
16
New cards
Midpoint Formula
The midpoint formula is a formula used to find the midpoint between two points in a coordinate plane. It is given by:
Midpoint = ((x1 + x2)/2, (y1 + y2)/2)
Where (x1, y1) and (x2, y2) are the coordinates of the two points.
Midpoint = ((x1 + x2)/2, (y1 + y2)/2)
Where (x1, y1) and (x2, y2) are the coordinates of the two points.
17
New cards
Slope Formula
The slope formula is used to calculate the slope of a line given two points on the line. It is expressed as:
`m = (y2 - y1) / (x2 - x1)`
where `m` is the slope and `(x1, y1)` and `(x2, y2)` are the coordinates of the two points.
`m = (y2 - y1) / (x2 - x1)`
where `m` is the slope and `(x1, y1)` and `(x2, y2)` are the coordinates of the two points.
18
New cards
Slope-Intercept Formula
y = mx +b
19
New cards
Multiplying Terms with Exponents
add the exponents
20
New cards
Dividing Terms with Exponents
subtract the exponents
21
New cards
Distributing Exponents
multiply the exponents
(4y)^2 = 4^2y^2 = 16y^2
(4y)^2 = 4^2y^2 = 16y^2
22
New cards
Negative Exponent
take the reciprocal and change the exponent to positive
(a/b) ^ -m = (b/a) ^ m
(a/b) ^ -m = (b/a) ^ m
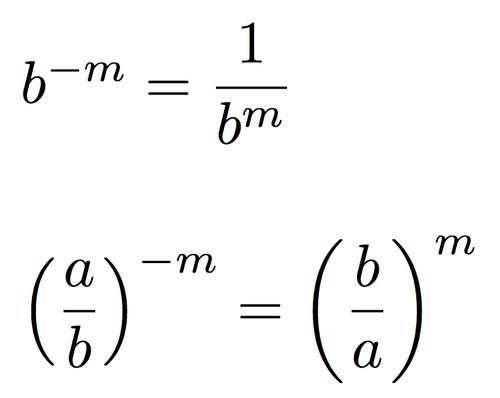
23
New cards
Positive Slope
rises from left to right
24
New cards
Negative Slope
falls from left to right
25
New cards
Volume of a Cube
V = s \* s \* s
V = s^3
V = s^3
26
New cards
Volume of a Rectangular Solid
V = LWH
27
New cards
Surface Area of a Cube
SA= 6s^2
28
New cards
Surface Area of a Rectangular Solid
SA = 2LW + 2LH + 2WH
29
New cards
Parallel Lines
same slope, different y intercept, no points in common
30
New cards
Secant Ratio - sec(A) … (1/cos)
1/cos(A) \= Hypotenuse/Adjacent
31
New cards
Cosecant Ratio - csc(A) (1/sin)
1/sin(A) \= Hypotenuse/Opposite
32
New cards
Cotangent Ratio - cot(A) … (1/tan) … (cos/sin)
1/tan(A) \= Adjacent/Opposite
33
New cards
Tan(A)
Sin(A)/Cos(A)
34
New cards
Percent Change
% change \= [(new value - old value)/ old value] x 100
35
New cards
what percent
x/100
36
New cards
is
\=
37
New cards
the product of
* (multiplication)
38
New cards
the sum of
\+ (addition)
39
New cards
(positive)*(negative)
\= (negative)
40
New cards
(negative)*(negative)
\= (positive)
41
New cards
Geometric Sequence
r = common ratio between terms (multiply or divide)
An example of a geometric sequence is: 2, 4, 8, 16, 32, ... where each term is obtained by multiplying the previous term by 2.
The formula for a geometric sequence is:
a_n = a_1 \* r^(n-1)
where a_n is the nth term, a_1 is the first term, r is the common ratio, and n is the number of terms.
An example of a geometric sequence is: 2, 4, 8, 16, 32, ... where each term is obtained by multiplying the previous term by 2.
The formula for a geometric sequence is:
a_n = a_1 \* r^(n-1)
where a_n is the nth term, a_1 is the first term, r is the common ratio, and n is the number of terms.
42
New cards
Arithmetic Sequence
d = common difference between terms (add or subtract)
The formula for an arithmetic sequence is:
`a_n = a1 + (n-1)d`
where `a_n` is the `n`th term, `a1` is the first term, `n` is the number of terms, and `d` is the common difference between consecutive terms.
The formula for an arithmetic sequence is:
`a_n = a1 + (n-1)d`
where `a_n` is the `n`th term, `a1` is the first term, `n` is the number of terms, and `d` is the common difference between consecutive terms.
43
New cards
Isosceles Triangle
two angles are equal, two sides are equal
44
New cards
Equilateral Triangle
three angles are equal (60 degrees), three sides are equal
45
New cards
Hypotenuse
Longest side in a right triangle, opposite the right angle
46
New cards
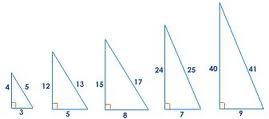
Pythagorean Triples
3, 4, 5 ; 5, 12, 13 ; 8, 15, 17 ; 7, 24, 25
47
New cards
Mean (average)
\= (sum of values) / (\# of values)
48
New cards
Median
middle number - put all numbers in order and pick the middle number
49
New cards
Mode
the number that occurs the MOST
50
New cards
Angles in a Triangle
the three interior angles add to 180 degrees
51
New cards
Y Intercept
y \= mx +b (y intercept is b; when x \= 0 what is y; where a line crosses the y axis)
52
New cards
Slope
change in y / change in x; rise / run
53
New cards
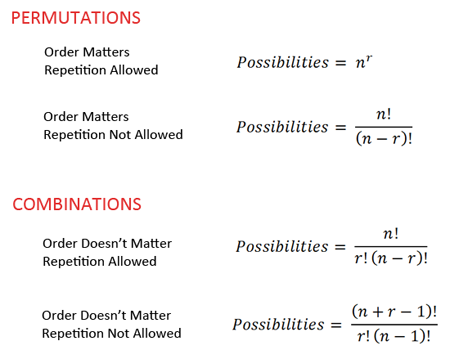
Permutations & Combinations
Use the dash method (ex. \_____ * \_____ * \_____ )
54
New cards
Distributing
3(2x + 5) = 6x+15
55
New cards
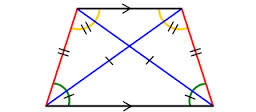
Properties of an Isosceles Trapezoid
-opposite sides are equal; -top two angles are congruent; -bottom two angles are congruent; -diagonals are congruent
56
New cards

Triangle Side Lengths
A side length of a triangle is: (1) greater than the other two sides subtracted; (2) less than the sum of the other two sides
57
New cards
Perpendicular lines
1 point in common, form a right angle, slope are negative reciprocals (i.e. 2/3 and -3/2)
58
New cards
Radians to Degrees
Multiply by (180/pi) or (pi/180) to change the units
59
New cards
180 degrees, 360 degrees
pi radians, 2*pi radians
60
New cards
Sin^2 + Cos^2 \= 1
1 - Sin^2 \= Cos^2, 1 - Cos^2 \= Sin^2
61
New cards
Weighted Average
\[(Av 1)(# 1) + (Av 2)(# 2) + (Av 3)(# 3) + (Av 4)(# 4)\] / (# of items)
A weighted average is a type of average that takes into account the importance, or weight, of each value in a data set. It is calculated by multiplying each value by its weight, adding up the products, and dividing by the sum of the weights. This is commonly used in finance, accounting, and statistics to calculate averages that reflect the relative importance of different values.
A weighted average is a type of average that takes into account the importance, or weight, of each value in a data set. It is calculated by multiplying each value by its weight, adding up the products, and dividing by the sum of the weights. This is commonly used in finance, accounting, and statistics to calculate averages that reflect the relative importance of different values.
62
New cards
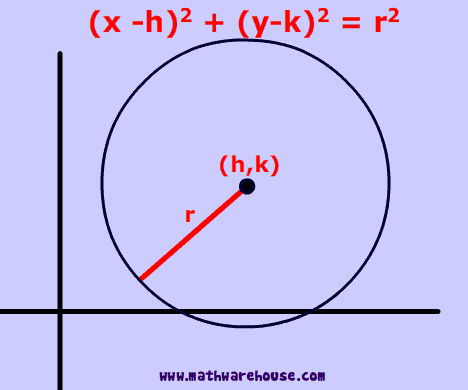
Equation of a Circle
\
(h, k) - center of the circle, r = radius
(h, k) - center of the circle, r = radius
63
New cards
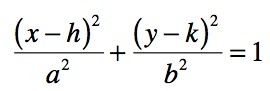
Equation of an Ellipse
(h, k) - center of the ellipse, a = x radius, b = y radius
64
New cards
Probability Equation
(Number of desired outcomes) / (Total number of outcomes)
65
New cards
Probability 2 events (AND)
Probability 1 * Probability 2 ( multiply)
66
New cards
Probability 2 events (OR)
Probability 1 + Probability 2 (ADD)
67
New cards
Factors
smaller numbers that evenly go into a larger number (i.e. For the number 12 here are the factors: 1, 2, 3, 4, 6, 12)
68
New cards
Multiples
larger than the number (i.e. For the number 12 here are the factors: 12, 24, 36, 48, ... )
69
New cards

Least Common Multiple (LCM)
70
New cards
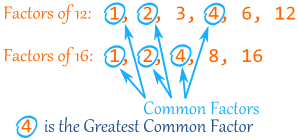
Greatest Common Factor (GCF)
71
New cards
Slope Formula
The steepness of a graph line; the ratio of the vertical change (the rise) to the horizontal change (the run).
72
New cards
What is the slope of the straight line passing through the points (-2,5) and (6,4)?
4-5/6\- -2\= -1/8, this graph will rise 1, and go left 8.
73
New cards
Slope-Intercept Formula
Ex: y\= -4/5 - 7. The graph will go up 4, and to the left 5, and the y-intercept will be -7.
74
New cards
Line
A straight path of points that extends forever in two directions. A line doesn't have any thickness or width. Arrows sometimes show that the line goes on forever in either direction
75
New cards
Line segment
The set of points on a line between any two points on that line.
76
New cards
Midpoint
The point halfway between two endpoints on a line segment.
77
New cards
Midpoint Formula
(x₁+x₂)/2, (y₁+y₂)/2
78
New cards
Intersect
To cross. Two lines can intersect each other much like two streets cross each other at an intersection.
79
New cards
Vertical Line
A line that runs straight up and down,
80
New cards
Horizontal Line
A line that runs straight across from left to right. *Think horizon
81
New cards
Parallel Lines
Lines that run in the same direction and keep the same distance apart. Parallel lines never intersect one another.
82
New cards
Perpendicular Lines
Two lines that intersect to form a square corner. The intersection of two perpendicular lines for a right, or 90-degree, angle
83
New cards
Ray
A part of a line, with one endpoint, that continues without end in one direction.
84
New cards
What are the angle facts?
1. No negative angle exists
2. no zero angle exists
3. its rare to see fractional angles
85
New cards
Right Angles
Angles that measure 90 degrees
86
New cards
Obtuse Angles
An angle whose measure is greater than 90 degrees and is less than 180 degrees.
87
New cards
Straight Angles
An angle that measures exactly 180 degrees and forms a straight line.
88
New cards
Complementary Angles
Two angles whose sum is 90 degrees
89
New cards
Supplementary Angles
Two angles whose sum is 180 degrees. Also, there is another 180 degrees below the line, with a total of 360 degrees.
90
New cards
Vertical Angles
Opposite angles with be equal to each other.
91
New cards
Reflex Angles
Angles that have measures greater than 180 degrees and less than 360 degrees
92
New cards
Angle Note
Angles around a point total 360 degrees.
93
New cards
Angle Note
The exterior angles of any figure are supplementary to the interior angles and always total 360 degrees.
94
New cards
Transversal
A line that intersects two or more lines
95
New cards
Vertical Angles
Angles that are opposite of each other have equal .
96
New cards
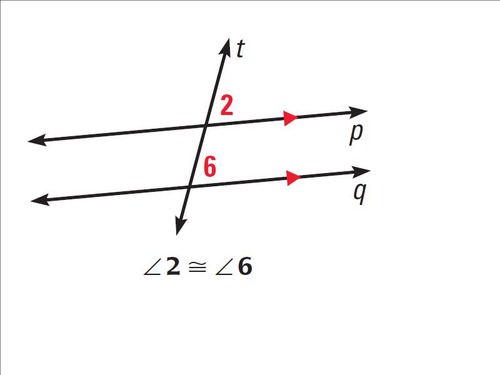
Corresponding angles
Angles in the same position around two parallel lines and a transversal and have equal measures.
97
New cards
Equilateral Triangle
A triangle with three congruent sides and three equal angles. Because the three angles must add up to 180 degrees, all three angles of an equilateral triangle are always equal to 60 degrees.
98
New cards
Isosceles Triangle
A triangle with two congruent sides. The angles opposite those sides are also equal . If angle A is 50 degrees, then angle B is also 50 degrees.
99
New cards
Scalene Triangle
A triangle with no congruent sides
100
New cards
Right Triangle
A triangle that has one inside angle that is 90 degrees.