resting membrane potential

general concepts

• Lab goal: examine how resting membrane potential (RMP) depends on extracellular K⁺ concentration.

• In the lab, you will measure resting membrane potential using electrodes.

• RMP definition: inside of cell is negative relative to the outside (extracellular = 0 mV by convention).

• Typical RMP values: −70 to −90 mV.

how to estimate number of charges involves

• To estimate charge separation:

  • Calculate cell surface area (from radius & shape).

  • Membrane capacitance per unit area is ~ 1 μF/cm² (constant across cells).

  • Total membrane capacitance:
    C_total = (capacitance/unit area) × (surface area).

• Use Coulomb’s law:
  Q = C × U, where
  Q = charge,
  C = capacitance,
  U = membrane potential.

• Elementary charge = 1.6 × 10⁻¹⁹ C → allows conversion of Q into number of ions.

• Also possible to estimate total ionic charge in a cell:

  • Intracellular ion concentration ~ 140 mM (for many ions).

  • Knowing cell volume allows calculation of total # ions.

• Comparison:

  • Only a tiny fraction of total ions participate in the membrane charge separation → important conceptual implication.

• Both intra- and extracellular solutions are electrically neutral overall, but at the membrane a very thin layer of charge is separated:

  • Inside surface = negative

  • Outside surface = positive

what determines rmp

1. Ion concentration gradients across the membrane
   (especially Na⁺, K⁺, Cl⁻)

2. Relative membrane permeabilities to those ions.

• Major ions considered: Na⁺, K⁺, Cl⁻ (others exist but less influential).

ionic asymmetry

• Intracellular concentrations:

  • K⁺ high, Na⁺ low.

• Extracellular concentrations:

  • K⁺ low, Na⁺ high.

• This asymmetry is established and maintained by:

  • Na⁺/K⁺ ATPase pump:

    • Pumps 3 Na⁺ out

    • Pumps 2 K⁺ in

    • Keeps intracellular K⁺ high, intracellular Na⁺ low.

how does ionic asymmetry + selective permeability = membrane potential

• With an ion gradient + membrane permeable only to one ion, a membrane potential must develop.

• Simplified 2-compartment model:

  • Both compartments start electrically neutral, same ions (K⁺, Cl⁻).

  • Membrane permeable only to K⁺.

  • One side has high K⁺, the other low K⁺.

1. Chemical force (concentration gradient) pushes K⁺ from high → low concentration side.

2. Receiving compartment becomes progressively more positive (K⁺ enters).

3. Donor compartment becomes progressively more negative (extra Cl⁻ left behind).

4. This creates an electrical force:

   • Positive compartment repels further K⁺ entry.

   • Negative compartment attracts K⁺ back.

5. Electrical force increases as charge separation grows.

6. At equilibrium:

   • Chemical force = electrical force (equal & opposite).

   • No net K⁺ movement.

   • The voltage at this point = equilibrium potential (E_K).

Nernst equation

• Physical chemist Nernst derived the equation relating equilibrium potential to ion concentration ratio.

• Full form includes:
  R (gas constant), T (Kelvin temperature), z (ion valence), F (Faraday constant).

• At room temperature, simplified:
  E = 58 mV × log₁₀([ion]ₒᵤₜ / [ion]ᵢₙ)

• Key points:

  • Depends only on ratio of concentrations.

  • Does not depend on permeability, as long as permeability is nonzero.

  • Each 10-fold change in [ion]ₒᵤₜ changes E by 58 mV

hypothesis in lab

• Hypothesis: at rest, membrane is permeable only to K⁺.

• If true:

  • Plotting RMP vs. log([K⁺]ₒᵤₜ) should produce a straight line (same slope as Nernst prediction: 58 mV/decade).

• Experimentally:

  • Plot shows a line, and experimental RMP values (circles) closely follow predicted E_K.

  • Not perfect match at low K⁺ concentrations.

Why imperfect agreement?

• Membrane is not exclusively permeable to K⁺.

• There is some Na⁺ permeability.

  • E_Na ≈ +50 to +60 mV (positive because [Na⁺]ₒᵤₜ is high, [Na⁺]ᵢₙ is low).

• Mixed Na⁺ permeability pulls RMP slightly more positive than pure E_K prediction.

effects of changing extracellular K+

• If [K⁺]ₒᵤₜ increases 10×, E_K becomes 58 mV more positive.

• If [K⁺]ₒᵤₜ increases 100×, E_K becomes 116 mV more positive (because 58 × 2).

• Result of the logarithmic relationship (semi-log plot).

recording setup

• muscle fibre (cylindrical), recording instruments.

• Two electrodes:

  • Bath electrode in the extracellular solution.

  • Glass microelectrode inserted into muscle fibre.

Glass microelectrode

• Glass, tapered tip.

• Filled with electrolyte.

• Inserted into the muscle cell to record electrical potential

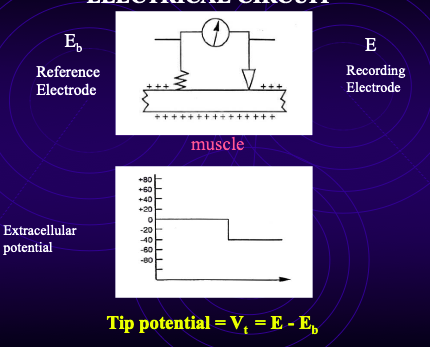
tip potential

• When the microelectrode is placed in the bath, the potential ≠ 0.

• You measure a tip potential (VT):

  • Caused by charges at the tip altering ionic environment inside vs outside electrode.

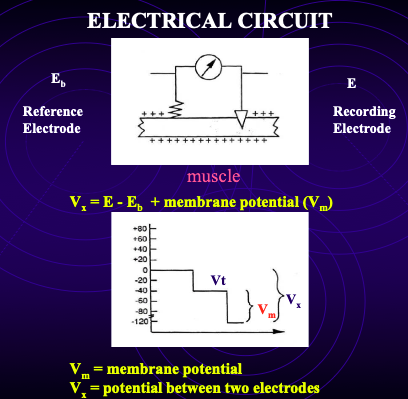
  • recording electrode - reference electrode

• Importance:

  • When electrode enters the cell, measured potential (VX) = RMP + tip potential.

  • Must subtract tip potential to obtain true RMP.

how to measure voltage

1. Place electrode in bath → record VT (tip potential).

2. Insert electrode into muscle fibre → measure VX.

3. RMP = VX – VT (aka potential between the two electrodes - (recording electrode - reference electrode))

electrode design requirements

Tip size

• Must be very small (~ 1 μm diameter).

  • Prevents physical damage to muscle fibre.

  • Large damage → intracellular fluid leaks out, extracellular fluid leaks in → disrupts measurements.

Tip size affects resistance

• Normal resistance for 1 μm tip ≈ 10 MΩ.

• If tip breaks → resistance decreases.

• If tip becomes plugged (e.g., connective tissue) → resistance increases

internal electrode solution

• Filled with 3 M KCl (very high concentration).

• High concentration needed to allow strong ionic current → good electrical contact.

• Why not NaCl?

  • If electrode leaks:

    • Na⁺ leak would dramatically alter intracellular Na⁺ concentration.

    • K⁺ leak is safer because cell already has high intracellular K⁺.

• Comparisons:

  • Intracellular K⁺ ≈ 140 mM.

  • Electrode KCl = 3 M (much higher).

recording instrument requirements

Equivalent circuit sketch

• Em = true resting membrane potential (modelled as a battery).

• Re = electrode resistance (≈10 MΩ).

• Ro = input resistance of recording instrument.

  

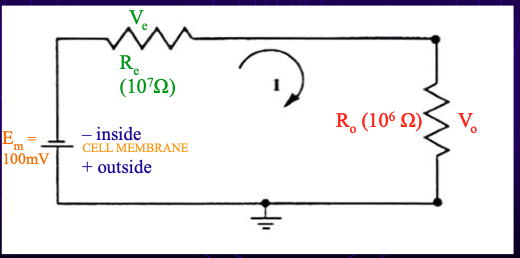
problem w oscilloscope

• Oscilloscope input resistance ≈ 1 MΩ.

• Measurement:

  • Voltage measured = voltage drop across RO.

  • Most voltage drops across RE instead → huge signal loss.

• Calculation:

  • RO = 1 MΩ, RE = 10 MΩ → total = 11 MΩ.

  • Only ~1/11 (~9%) of true RMP is recorded.

• Conclusion: oscilloscope alone is not suitable.

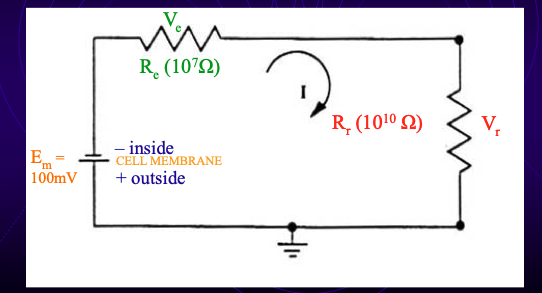
solution to problem with oscilloscope

• Use amplifier where RO is very large (≥ 10¹⁰ Ω; in reality ~10¹⁴ Ω).

• Then:

  • RO >> RE → nearly all voltage drop across RO.

  • Ratio RO / (RE + RO) ≈ 1.

  • Measured voltage ≈ true RMP.

why is high input resistance necessary

Accurate RMP measurement

• Minimizes voltage loss across electrode.

2. Reduces current flow through electrode

• High current → lots of ion movement → disturbs intracellular environment.

• Want minimal disturbance.

3. Electrode resistance often changes

• When entering/leaving the cell, brushing tissue, plugging, etc.

• High RO ensures changes in RE do not affect recorded RMP.

  • Because RO >> RE, even if RE changes from 10 → 1 or 20 MΩ, proportion stays ~1.

potassium vs sodium equilibrium potentials

• EK ≈ –90 mV (example: –90 to –110 mV range).

• ENa ≈ +60 mV.

If membrane were equally permeable to K⁺ and Na⁺

• RMP would be halfway between:

  • (–90 + +60) / 2 = –15 mV.

If membrane permeable only to K⁺

• RMP = EK ≈ –90 mV.

If membrane permeable only to Na⁺

• RMP = ENa ≈ +60 mV.

In reality

• Membrane is much more permeable to K⁺, so RMP is close to EK.

experimental procedure

1. Record RMP at low extracellular K⁺.

2. Increase extracellular K⁺ stepwise (5 different concentrations).

3. Measure RMP at each condition.

4. Graph the relationship:

   • Does RMP follow predicted Nernst-like slope?

5. Perform statistical tests:

   • Compare low vs high K⁺.

   • Use t-tests, p-values.

TEA experiments

• TEA blocks some K⁺ channels → reduces K⁺ conductance.

• What should happen if K⁺ is fully blocked?

  • RMP ≈ ENa (≈ +60 mV), and changes in external K⁺ would have no effect.

• But TEA does not block all K⁺ channels:

  • Many potassium channel subtypes (different conductance, pharmacology, open times).

  • TEA blocks only some of them → partial conductance remains.

What you will observe

• With TEA:

  • K⁺ conductance decreases → RMP becomes less dependent on extracellular K⁺.

  • RMP shifts toward more positive values (toward ENa).

  • But does not reach +60 mV because some K⁺ channels still function.