CO1.1 Real Numbers and the Real Number System

What types of numbers make up the real number system?

Natural numbers

It consists of the natural numbers together with their negatives and 0

Integers

We construct these numbers by taking ratios of integers.

Rational numbers

Any rational number r can be expressed as…

r = m/n

where m and n are integers and n ≠ 0

The given is an example of _______.

1, 2, 3, 4, ...

Natural numbers

The given is an example of ______.

…, -3, -2, -1, 0, 1, 2, 3, …

Integers

The given is an example of ______.

1/2, 5/3, -3.5

Rational numbers

Any number divided by zero is generally __________

undefined

0/0 is a special case. It is called _______ because it doesn’t have a single, _______ _______. It can potentially represent any number, depending on the context in which it arises.

Indeterminate; definite value

The set of all real numbers is usually denoted by the symbol ____

R

T or F: Every decimal number has a decimal representation. If the number is rational, then its corresponding decimal is repeating.

True

T or F: If the number is irrational, the decimal representation is non-repeating.

True

T or F: The image shown are examples of irrational numbers.

True

What are the properties of real numbers?

• Commutative property

• Associative property

• Distributive property

A property wherein when we add or multiply two numbers, order doesn’t matter.

Commutative property

A property wherein when we add or multiply three numbers, it doesn’t matter which two we add or multiply first.

Associative property

A property wherein when we multiply a number by a sum of two numbers, we get the same result as we get if we multiply the number by each of the terms and then add the results.

Distributive property

T or F: Every nonzero real number has a multiplicative inverse, 1/a, that satisfies a x 1/a = 1.

True

T or F: 1/a is commonly called the reciprocal of a.

True

Real numbers can be represented by points on a line, also known as a ____ _______ _____.

real number line

A set of numbers between two points.

Intervals

What are the properties of absolute values?

1. The absolute value of a number is always positive or zero

2. A number and its negative have the same absolute value

3. The absolute value of a product is the product of the absolute values

4. Triangle inequality

If a and b are real numbers, then the distance between the points a and b on the real line is

d(a, b) = |b - a|

What are the laws of exponents?

1. Product rule

2. Quotient rule

3. Power of a power

4. Power of a product rule

5. Power of a quotient rule

6. Zero exponent rule

7. Negative exponent rule

8. Fractional exponent rule

To multiply two powers of the same number, add the exponents

a^maⁿ = a^m+n

Product rule

To divide two powers of the same number, subtract the exponents

a^m/aⁿ = a^m-n

Quotient rule

To raise a power to a new power, multiply the exponents

(a^m)ⁿ = a^mn

Power of a power rule

To raise a product to a power, raise each factor to the power

(ab)ⁿ = aⁿbⁿ

Power of a product

To raise a quotient to a power, raise both numerator and denominator to the power

(a/b)ⁿ = aⁿ/bⁿ

Power of a quotient

To raise a fraction to a negative power, invert the fraction and change the sign of the exponent

(a/b)^-n = (b/a)ⁿ or a^-n = 1/aⁿ

Negative exponent

To move a number raised to a power from numerator to denominator or from denominator to numerator, change the sign of the exponent

a^-n/b^-m = b^m/aⁿ

Any real number raised to zero will equal to 1.

a⁰ = 1

Zero exponent

a¹ = a

Identity exponent

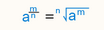
What law of exponents is shown?

Fractional exponent

________ is the opposite of an exponent that is represented with a symbol '√' also known as root. It can either be a square root or a cube root and the number before the symbol or radical is considere to be an _____ _____ or _______.

Radical; index number or degree

A number or expression inside the radical symbol.

Radicand

We use the concept of radicals to define numbers with _____ or ______ exponents.

fractional; rational

The given is an example of?

a^m/n = (ⁿ√a )^m or equivalently a^m/n = ⁿ√a^m

Rational exponents