8.1 Hypothesis Testing One Sample

Steps for Hypothesis testing for Proportion

1. Assumptions

2. Stating Hypothesis

3. Test Statistic

4. Calculate P Value

5. Conclusion

Assumptions

Check what assumptions are needed for each specific significnace test

Hypothesis

Statement about a population, claiming that a parameter takes a particular numerical value or falls in a certain range of values

Null Hypothsis

Specifies a single value

Usually represents no effect

Alternative Hyphothesis

Specify a range of values

Usually represent some type of effect

Test’s Side

Not Equal = Both Sides

Larger = Right Sided

Smaller = Left Sided

Test Statistic

Describe how far the point estimate falls from the parameter value in the null hypothesis, measured by number of standard errors

P Value

Probability to receive the value equal to the test statistic or more extreme, given H0 is true.

If P value is small, H0 may be false or the sample is not representative of the population

Significant Level (\alpha)

If p value is <= \alpha reject H0, others H0 is true.

Propotion Assumptions

• Variable measured is Categorical

• Data obtained using randomization

• np0(1-p0) >= 5

Proportion Test Statistics

Mean Assumption

• Variable measured is quantitative

• Data obtained using randomization

• Population distribution is approximately normal (ignored when n > 30)

Mean Test Statistic Formula

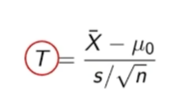
Conditions where the Confidence Interval and Significance Test is Consistent

• Confidence level, 95%, must match the significance level, 0.05

• Test must be a 2-sided test

• CI and test must use the same standard error (For proportion)

Obtaining T-Test in R

t.test(vector, mu=x)

Alternative = “two.sided”

conf.level = 0.95

Type 1 Error

Reject H0 when H0 is true. Probability of this is \alpha. Focus on type 1 error.

Type 2 Error

Fail to reject Ho even tho it is false. Probability is \beta, power of a test = 1 - \beta.