Sample and Probability space, counting principles, set operations and probability rules, conditional prob and independence, random variables, expectation and variance

What is the sample space?

The sample space (Omega (Ω)) is a set of all possible outcomes. Hence a single outcome (lowercase omega (ω)) is an element of Ω

What’s the sum to infinity of a geometric series?

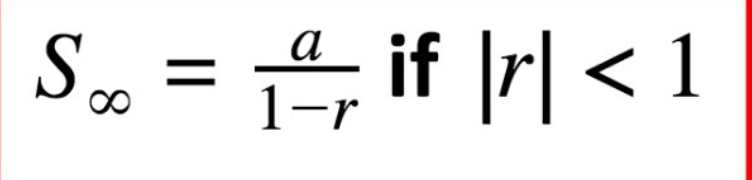
What does a probability space consist of?

What is Discrete Probability?

A sample space that is either finite or countable.

What is the power set in discrete probability?

The event space F is the power set of \Omega, ie. The the set of all subsets, often denoted by2^{\Omega}.

• We never have to check if an event A is in F (it will always be true if A is a subset of \Omega).

• Because \Omega is countable, we can pick elements one by one and we will eventually have picked all the elements, allowing us to define the probability of any event as the sum of probabilities of individual outcomes.

How can we calculate the probability for equally likely outcomes?

Let \Omega Be finite. The outcomes are equally if there’s a constant c\in\left(0,1\rbrack\right. such that P({\omega}) = c for all \omega\in\Omega

c=\frac{1}{\left\vert\Omega\right\vert}

Therefore the probability of an event E = \frac{\left\vert E\right\vert}{\left\vert\Omega\right\vert}

How can we work out how many ways there are of ordering n elements

n! = n(n-1)(n-2)…x2×1

BY CONVENTION 0! =1

Permutation formula: how many ways are there to order k elements from a set of n?

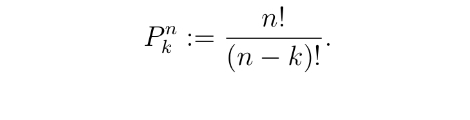
How do we work out how many ways are there to choose k elements from a set of n?

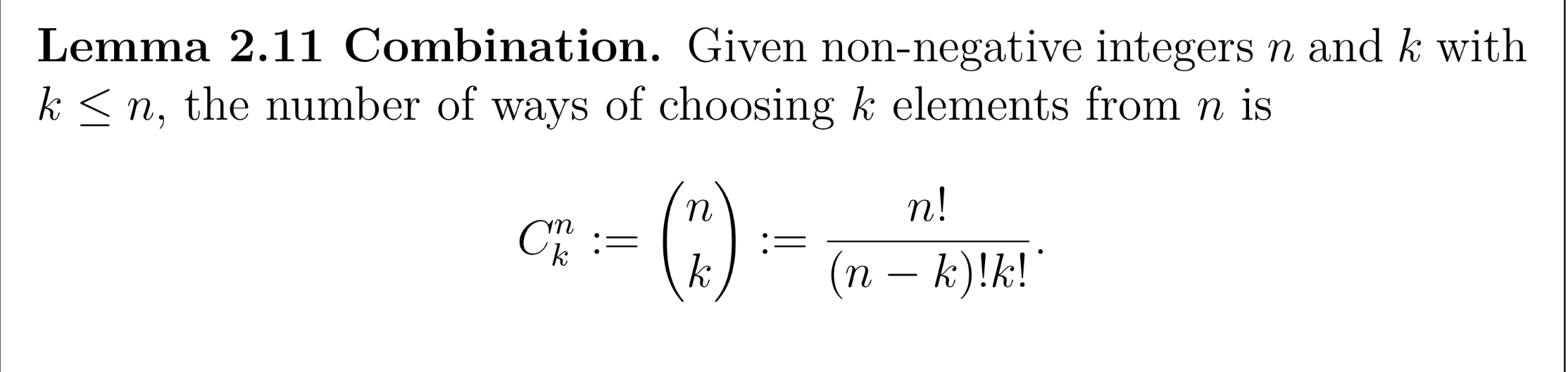
What does A\B mean?

The set of elements from A that are not in B

How can you re write A\cup\left(B\cap C\right) and A\cap(B\cup C)

(A\cup B)\cap(B\cup C)

\left(A\cap B)\cup\left(B\cap C\right)\right)

What are Kolmogorov’s Axioms

How do we work out P(B|A)

P(B\vert A)=\frac{P(A\cap B)}{P(A)}

What does P(C\cupB|A) equal

= P(C\vert A)+P\left(B\vert A\right)-P\left(C\cap B\vert A\right)

If P(B\capA) >0, what does P(CnBnA) equal with regards to conditional events

P\left(C\cap B\cap A\right)=P\left(C\vert B\cap A\right)\cdot P\left(B\vert A\right)\cdot P\left(A\right)

We can generalise this to as many events as we want. Let \left(A_{i}\right)_{i=1}^{n} be a finite sequence of events.

Then P\left(\cap_{i=1}^{n}A_{i}\right)=\left(\Pi_{i=2}^{n}P\left(A_{i}\vert\cap_{k=1}^{n-1}A_{k}\right)\right).p\left(A_1\right)

What is a partition?

A finite sequence of events \left(A_{i}\right)_{i=1}^{n} Is called a partition of \Omega If \left(A_{i}\right)_{i=1}^{n} are disjoint and \Omega =\cup_{i=1}^{n}A_{i}

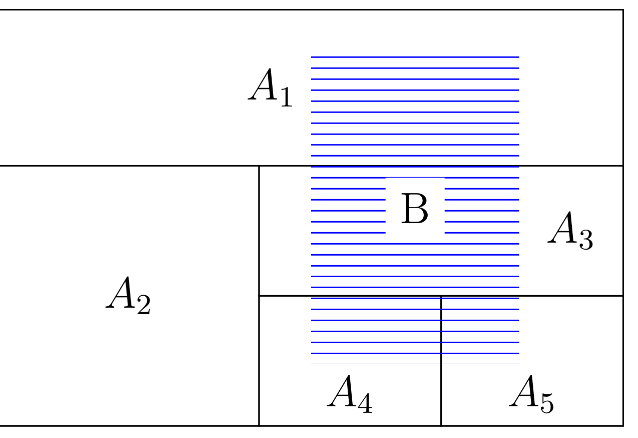
What is the Law of Total Probability ?

Let \left(A_{i}\right)_{i=1}^{n} Be a partition of \Omegasuch that P\left(A_{i}\right)>0. Let B be an event. Then

P\left(B\right)=\sum_{i=1}^{n}P\left(B\cap A_{i}\right)

=\sum_{i=1}^{n}P\left(B\left|A_{i}\right.\right)\cdot P\left(A_{i}\right)

What is Baye’s Rule?

If P(A),P(B) > 0 then

P\left(A\vert B\right)=P\left(B\vert A\right)\cdot\frac{P\left(A\right)}{P\left(B\right)}

Baye’s rule reverses the order of the conditional probability.

How do we know if events A and B are independent?

If P(AnB) = P(A) x P(B)

What is mutual independence?

A finite sequence of events \left(A_{i}\right)_{i=1}^{n} mutually indeppendent if for every non-empty subset I\subseteq\left\lbrace1,2,3,\ldots,n\right\rbrace

P\left(\cap_{i\in I}A_{i}\right)=\Pi_{i\in I}P\left(A_{i}\right)

E.g. when n=3

P(AnB) = P(A) x P(B)

P(AnC) = P(A) x P(C)

P(BnC) = P(B) x P(C)

P(AnBnC) = P(A) x P(B) x P(C)

What is a Probability Mass Function?

A Probability Mass Function (pmf) gives the probability that a discrete random variable takes on each possible value.

Formally, if X is a discrete random variable, its pmf is:

P_{X}(x)=P(X=x)

What does it mean for two random variables to have the same distribution?

They have the same pmfs.

X~Y (“X distribute like Y”) if P_{X}\left(x\right)=P_{Y}\left(y\right)

Two random variables with the same distribution are typically not equal.

What is a joint probability mass function?

The joint probability mass function of X and Y is

P_{X,Y}\left(x,y\right)=P\left\lbrack X=x,Y=y\right\rbrack

=P\left(\left\lbrace X=x\right\rbrace\cap\left\lbrace Y=y\right\rbrace\right)

The joint pmf contains the information of the mass functions for X and Y

What are pairwise independent Random variables with respect to discrete RVs?

We say the discrete random variables are independent if

P_{X,Y}\left(x,y\right)=P_{X}\left(x\right)\times P_{Y}\left(y\right)for all x,y\in\mathbb{R}

What is the distribution function?

The distribution function of a random variables X is

F_{X}\left(x\right)=P\left\lbrack X\le x\right\rbrace for x,y\in\mathbb{R}

The joint distribution function of two RVs X and Y is

F_{X,Y}\left(x,y\right)=P\left\lbrack X\le x,Y\le y\right\rbrack

The distribution function is often called the cumulative distribution function function (cdf)

What is the expectation of a discrete RV?

E\left\lbrack X\right\rbrack=\Sigma_{x\in R\left(X\right)}x\times P\left\lbrack X=x\right\rbrack

Considering RVs X and Y, what’s the expectation of a function g:R→R and a bivariate function h:RxR→R?

E\left\lbrack g\left(X\right)\right\rbrack_{}=\sum_{x\in R_{X}}g\left(x\right)\times P_{X\left(x\right)}

E\left\lbrack h\left(X,Y\right)\right\rbrack=\sum_{x\in R_{X}}\sum_{y\in R_{Y}}h\left(x,y\right)\times P_{X,Y}\left(x,y\right)

What does E\left\lbrack aX+b\right\rbrack=?

a\times E\left(x\right)+b

What does E\left\lbrack X+Y\right\rbrack=? For the random variables X and Y

E\left\lbrack X\right\rbrack+E\left\lbrack Y\right\rbrack

When does E\left\lbrack XY\right\rbrack=E\left\lbrack X\right\rbrack\times E\left\lbrack Y\right\rbrack Always?

When X and Y are independent

What is the variance of a random variable X?

How spread out a probability distribution is.

Formula for Var(X)

Var\left(X\right)=E\left\lbrack\left(X-E\left\lbrack X\right\rbrack\right)^2\right\rbrack

Or more usefully

Var\left(X\right)=E\left\lbrack X^2\right.]-E\left\lbrack X\right\rbrack^2

What’s the standard deviation (SD(X)) of a RV X?

SD\left(X\right)=\sqrt{Var\left(X\right)}

What does Var(aX+b) equal when X is a random variable with finite variance?

Var(aX+b)=a² x Var(X)

When does Var(X+Y) always equal Var(X) + Var(Y)?

When X and Y are independent.