Systems of Linear Equations
1/20
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
21 Terms
Standard Form of 2 Equations with 2 Variables
𝑎1𝑥 + 𝑏1𝑦 = 𝑐1
𝑎2𝑥 + 𝑏2𝑦 = 𝑐2
where 𝑎1, 𝑎2, 𝑏1 , 𝑏2 are coefficients of variables 𝑥 and 𝑦, respectively, and 𝑐1, 𝑐2 are constants
Set of Solutions
set of all ordered n-tuples of numbers that make each equation a true statement
Equivalent
two linear systems that have the same solution set
Solving with 2 Variables
basic approach - simplify the problem by eliminating one of the variables, and finding the other
substituting
subtracting
equating
Substituting Example
Let us go back to our set of equations:
𝑥 + 2𝑦 = 5
3𝑥 + 9𝑦 = 21
In the first equation we can isolate 𝑥 to obtain: 𝑥 = 5 − 2𝑦
We can now substitute the top equation for 𝑥 into the second equation:
3 (5 − 2𝑦) + 9𝑦 = 21
We have just eliminated one of the variables, i.e., 𝑥, by substitution
15 − 6𝑦 + 9𝑦 = 21
3𝑦 = 6
𝑦 = 2
𝑥 = 5 − 2 ∙ 2 = 1
Solution <x, y> = <1, 2>
Subtracting Example
𝑥 + 2𝑦 = 5
3𝑥 + 9𝑦 = 21
Observe that the first equation’s truth remains if we were to multiply it by some constant, i.e., 3
3𝑥 + 6𝑦 = 15
3𝑥 + 9𝑦 = 21
If we subtract two true equations from each other we obtain another true equation.
3𝑥 + 9𝑦 − 3𝑥 − 6𝑦 = 21 − 15
3𝑦 = 6
𝑦 = 2
𝑥 + 2 ∙ 2 = 5
𝑥 = 1
Solution <x, y> = <1, 2>
Equating Example
𝑥 + 2𝑦 = 5
3𝑥 + 9𝑦 = 21
We can isolate 𝑥 in both equations:
𝑥 = 5 − 2𝑦
𝑥 = (21 − 9𝑦)/3 = 7 − 3𝑦
The variable 𝑥 is still unknown, but we know two facts about it
𝑥 = 5 − 2𝑦 = 7 − 3𝑦; by adding 3𝑦 to both sides of the last equation:
5 + 𝑦 = 7; by subtracting 5
𝑦 = 7 − 5 = 2
𝑥 = 5 − 2 ∙ 2 = 1
Solution <x, y> = <1, 2>
Solving with 2 Variables Graphically
Representing the set of solutions of a system of two linear equations:
𝑎1𝑥 + 𝑏1𝑦 = 𝑐1
𝑎2𝑥 + 𝑏2𝑦 = 𝑐2
set of points in ℝ2 satisfying both equations simultaneously
the intersection of the two lines in ℝ2
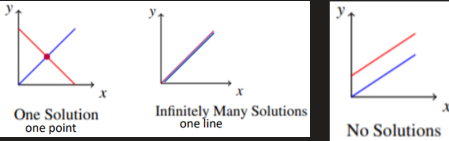
Types of Solutions with 2 Variables
A system of linear equations in which at least one of the coefficient is 𝑎 or 𝑏 ≠ 0 has
exactly one solution, or
infinitely many solutions, or
no solution
A system of linear equation is consistent if it has either one solution or infinitely many solutions
A system of linear equation is inconsistent if it has no solution
Solving with 3 Variables
Representing the set of solutions of a system of three linear equations:
𝑎1𝑥 + 𝑏1𝑦 + 𝑐1𝑧 = 𝑑1
𝑎2𝑥 + 𝑏2𝑦 + 𝑐2𝑧 = 𝑑2
𝑎3𝑥 + 𝑏3𝑦 + 𝑐3𝑧 = 𝑑3
set of points in ℝ3 satisfying all three equations simultaneously
the intersection of the three planes in ℝ3
Solutions with 3 Variables
A system of linear equations in which at least one of the coefficient is 𝑎 or 𝑏 or 𝑐 ≠ 0 has
exactly one solution, or
infinitely many solutions, or
no solution
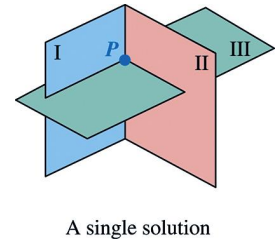
Consistent System of 3 Linear Equations with 1 Solution
one point
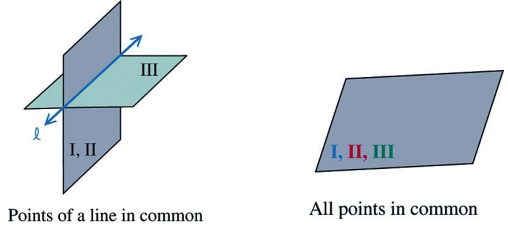
Consistent System of 3 Linear Equations with Infinitely Many Solutions
one line or one plane
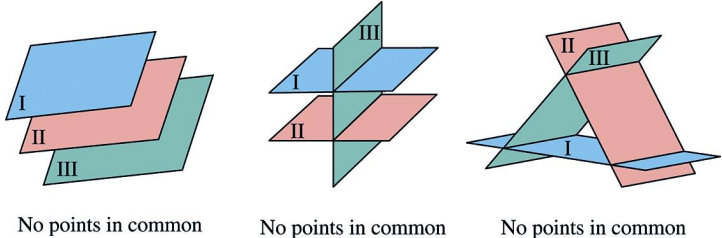
Inconsistent System of 3 Linear Equations with no Solution
Solving with n Variables
Basic algebraic approach: simplify the problem by eliminating one of the variables, and finding the other
substituting
subtracting
equating
Advanced systematic approach: Gauss-Jordan elimination algorithm
Coefficient Matrix
Let’s us have:
𝑥 + 2𝑦 + 3𝑧 = 6 | 1 ∙ 𝑥 + 2 ∙ 𝑦 + 3 ∙ 𝑧 = 6 |
𝑥 − 𝑦 + 𝑧 = 1 | 1 ∙ 𝑥 − 1 ∙ 𝑦 + 1 ∙ 𝑧 = 1 |
2𝑥 + 3𝑦 + 4𝑧 = 9 | 2 ∙ 𝑥 + 3 ∙ 𝑦 + 4 ∙ 𝑧 = 9 |
The coefficient matrix:
𝐴 ∈ ℝ𝑚 × 𝑛, a rectangular array of real numbers, with 𝑚 rows and 𝑛 columns
one row for each equation
one column for the coefficients of each variable, i.e., 𝑥, 𝑦 and 𝑧
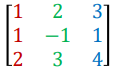
Augmented Matrix
Let’s us have:
𝑥 + 2𝑦 + 3𝑧 = 6 | 1 ∙ 𝑥 + 2 ∙ 𝑦 + 3 ∙ 𝑧 = 6 |
𝑥 − 𝑦 + 𝑧 = 1 | 1 ∙ 𝑥 − 1 ∙ 𝑦 + 1 ∙ 𝑧 = 1 |
2𝑥 + 3𝑦 + 4𝑧 = 9 | 2 ∙ 𝑥 + 3 ∙ 𝑦 + 4 ∙ 𝑧 = 9 |
The augmented matrix:
∈ ℝ𝑚 × (𝑛 + 1)
one row for each equation
one column for the coefficients of each variable, i.e., 𝑥, 𝑦 and 𝑧
one final column for constant terms, after the vertical line
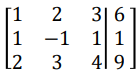
Gauss-Jordan Elimination Algorithm
start with a system of linear equations expressed as augmented matrix
perform row operations to transform the matrix in equivalent forms
swap the position of 2 rows
multiply a row by a non 0 constant
add a multiple of one row to another row
end result - reduced row echelon form of the matrix
Reduced Row Echelon Form
The leading entry in a row of a matrix is the first non-zero entry in that row, starting from the left:
all nonzero rows are above any rows of all zeros
each leading entry of a row is in a column to the right of the leading entry of the row above it
all leading entries in each non zero row are 1
all entries in a column below leading entry are zero
all entries in a column above leading entry are zero (1, 2, 3 in row echelon form)

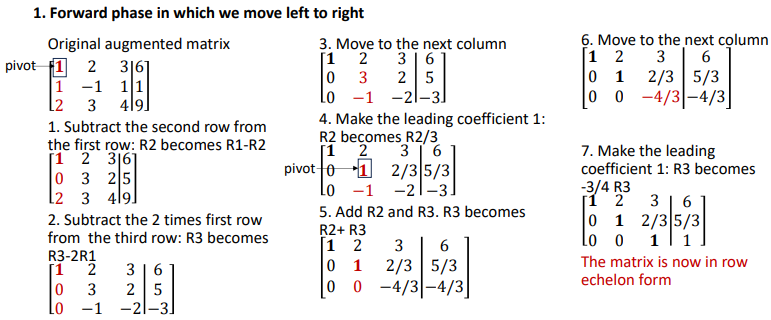
Forward Phase (left to right)
Obtain a pivot (a leading one) in the leftmost column
Subtract/add the row with the pivot from all rows below it, to obtain zeros in the entire column
Look for a leading one in the next column to the right and Repeat
Outcome: row echelon form
Backward Phase (right to left)
Find the rightmost pivot and use it to eliminate all numbers above the pivot in its column
Move one column to the left and Repeat
Outcome: reduced row echelon form
