Section 3.3 - Cramers Rule, Adj(A) & Volume/Area

When does Cramers rule apply?

Only when A is a square matrix and the determinant of that matrix does not = 0. This guarantees a unique solution for Ax=b.

Cramers Rule formula for the solution of Ax=b.

If A is inveritble, the system Ax=b has a unique solution, and each componenet is:

Ai(b) is formed by replacing ith column of A by the vector b.

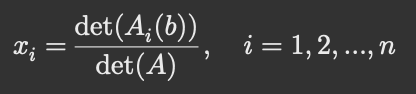
What does Ai(b) mean?

Ai(b) is formed by replacing ith column of A by the vector b.

What happens if detA = 0 when solving Ax=b

The system does not have a unique solution.

It either has no solutions or infinitely many solutions

Hoe to determine solution type when detA = 0.

If some det(Ai(b) doesnt equal 0 then no solution (inconsistent)

If all det(Ai(b)) = 0 then Infinitely many solutions.

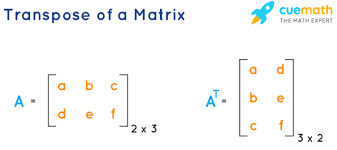
Defintion of adj(A)

adj(A) is the transpose of the cofactor matrix of A.

Transpose example is in the picture

Inverse formula using adj(A) - (Theorem 8)

If det(A) does not = 0, then the inverse of a nxn matrix:

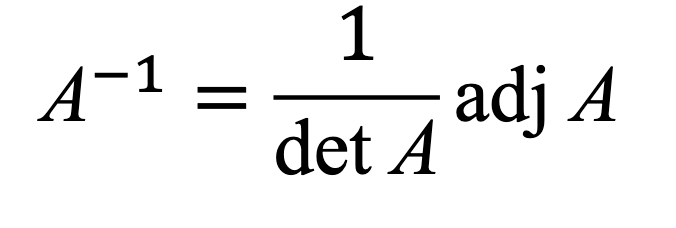
If A is a 2×2 matrix, how do we determine the area of the parallelogram? (Theorem 9)

The area is of the parallelogram determined by the columns of A is the absolute value of detA

Geometric meaning of |det(A)|

|det(A)| is the scaling factor for area (In R²) or volume (in R³)

What is a 3×3 diagonal matrix?

Just is the basis vectors, basically an identity matrix.

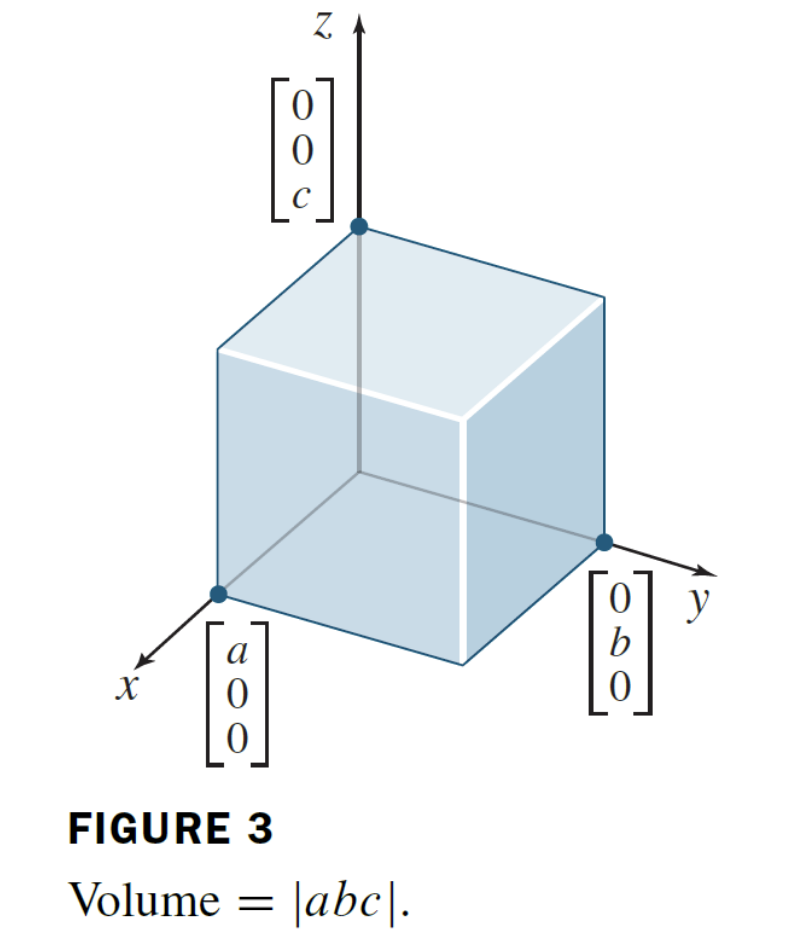
How can we scale an Area of a matrix in R² or R³ (Theorem 10)

We can just take the |determinant| of that space and than scale it by the scale factor. Multiply them

Area of parallelogram from vectors u and v?

Area = |det([u,v])|

What does a negative determinent mean?

The transformation flips orientation (reflection).

Hoe to get edge vectors from four vertices.

Pick one vertex, subtract that vertex from other vertices, forming vectors u, v, w. Then use area/volume formulas.