Management accounting & Controlling

Economics

• Production, distribution/exchanges and consumption of goods and services/resources

Finance/Financial economics

• Money transactions

Corporate Finance

• Funding businesses

Finance

• Financing – 2 angles: finance-user and finance-provider

• Business strategy – decision tool

Accounting

• Collecting Analysing Communicating management data

• Set of tools

2 main categories

• Management accounting

• Financial accounting/reporting >> stakeholders

Share of a population (measure)

percentage

growth (measure)

percentage & percentage points

margin vs. result (profit/loss) (measure)

• percentage 

• percentage points 

interests rate (measure)

inflation — purchasing power

calculation for percentages

1- 1000/3000= 1 - 0,3334 = 0,667

calculation for percentages— 

100 × 1800 : 3000 = 60 —> 60%

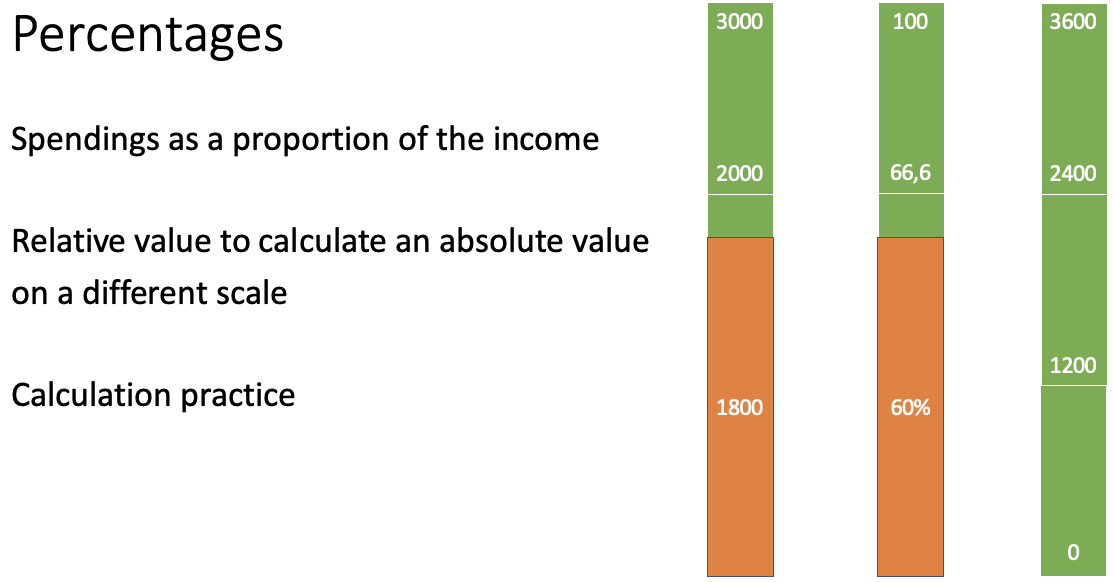
Percentages— spendings as a proportion of the income

How much is 60% of 3600? 

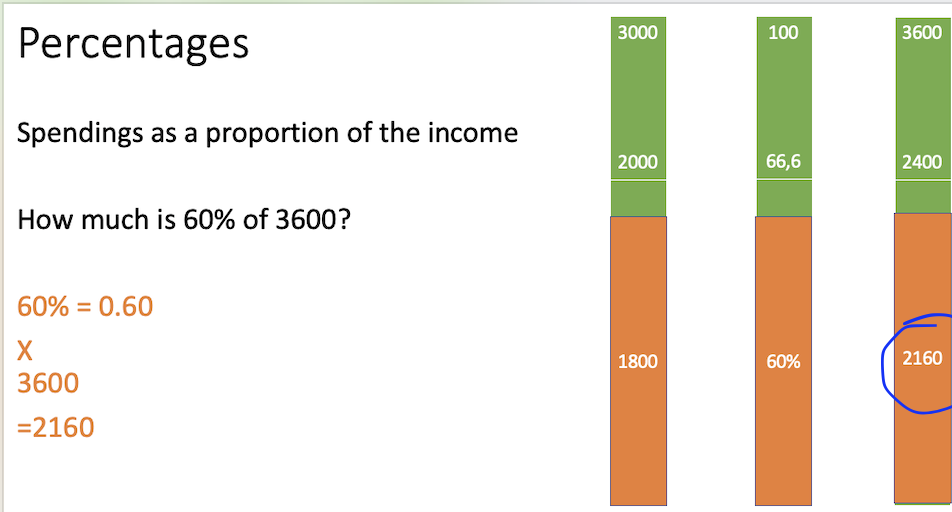
60% = 0.60 X 3600 =2160

Note on numbers— European vs. Anglosaxon

European vs. Anglosaxon

• 0,2 <> 0.2

• 1.000 <> 1,000

Note on numbers— Accountants vs mathematicians

• (56) <> -56

• 1k <> 1,000

Share of a population

Population:

In statistics, a population is a representative sample of a larger group of people or even things with one or more characteristics in common.

What percentage of total luxury spendings for each category?

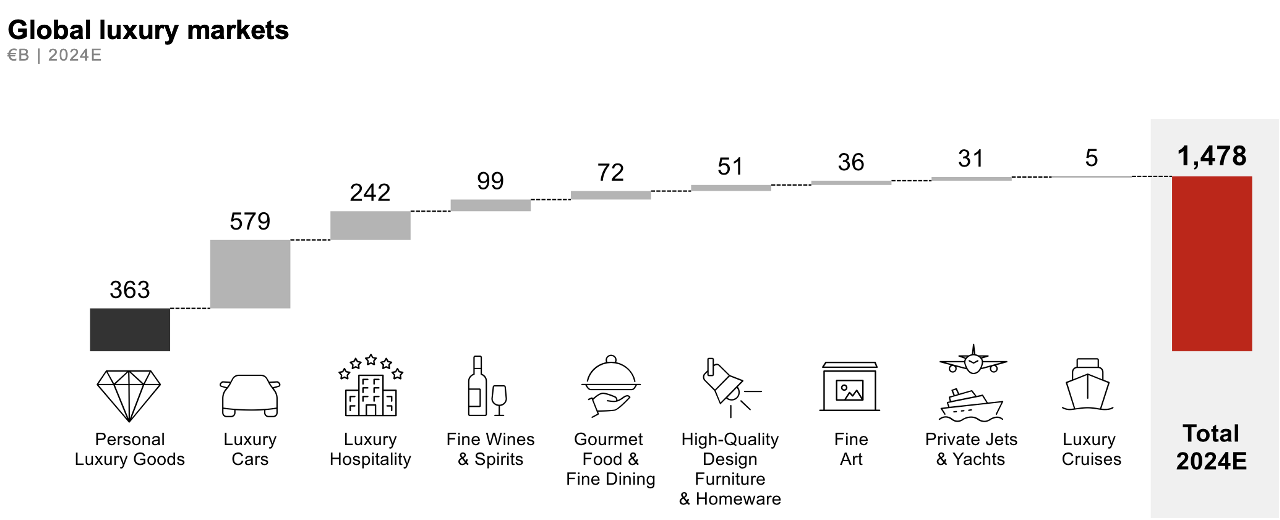
Absolute value of a category Divided by Absolute value of total spendings = Proportion expressed as a decimal

• 363/1,478 = 0.2456… = 0.25

  • 0.25 = 25%

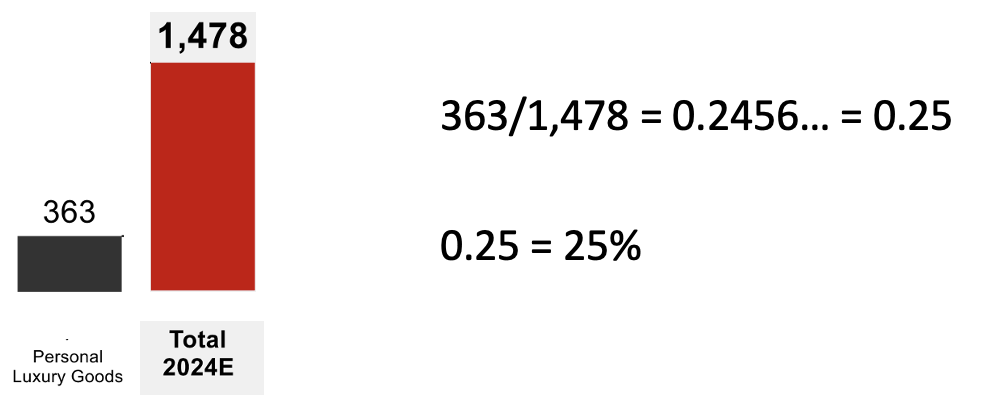
What percentage of total luxury spendings for each category ? 

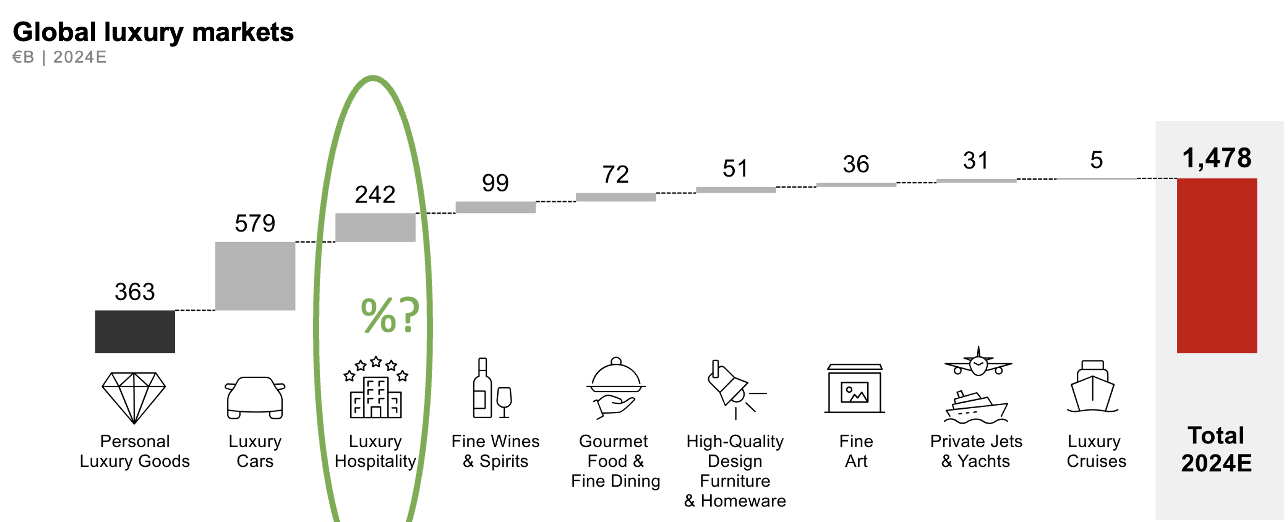
Absolute value of a category Divided by Absolute value of total spendings = Proportion expressed as a decimal

• 242/1,478 = 0.1637… = 0.16

  • 0.16 = 16%

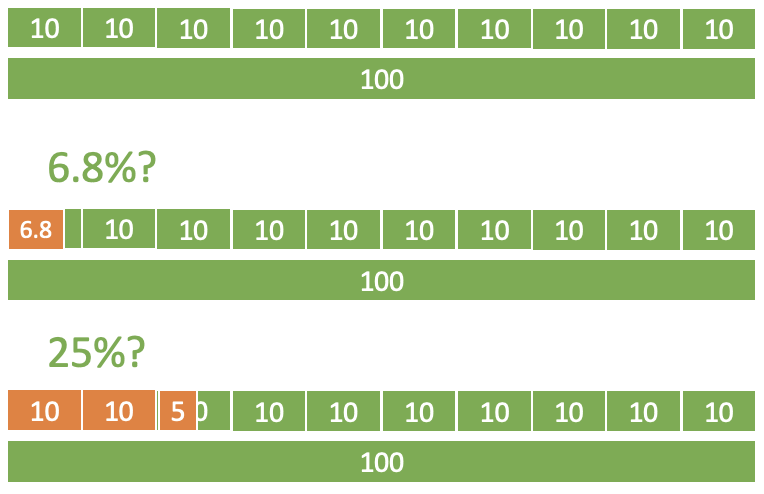
Visualizing the meaning: Share of a population— What does 6.8% mean ? 

Visualizing the meaning: Share of a population— What does 25% mean ? 

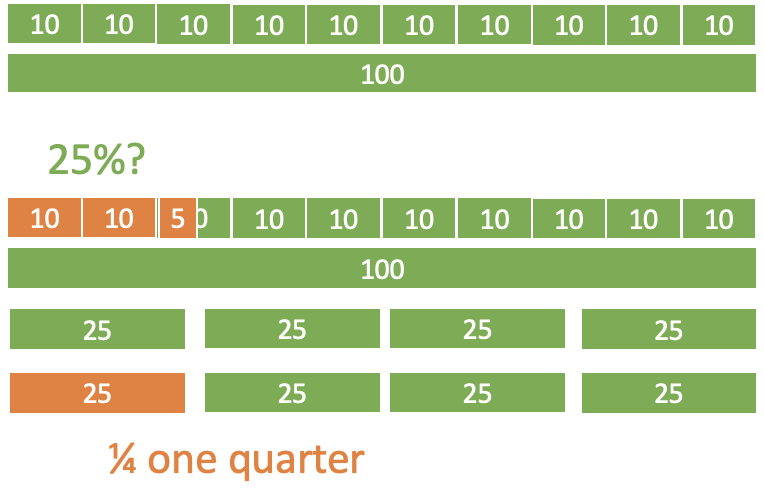
fractions 

Percentage of increase formula #1

with actual value

Percent increase formula #2

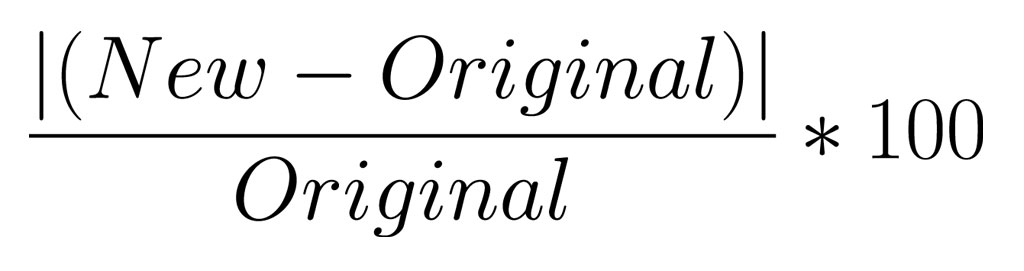
with percentages

If spendings are stable in proportion of total spendings and the following year total spendingsare 1600 billion euros

How much is spent on personal luxury goods?

25% times 1600 = 0.25 x 1600 = 400

(Previously 363)

Percentage variation def

Percentage to reflect the evolution of any given quantity

• (vs what we looked at which is a proportion/shareof a population)

formula

• Variation to be compared with the original value

• Variation/original value = 0,XX = XX%

Sales variation— percentages 

Percentage variation:

FORMULA: (difference between Final and orignialvalue)/original value

ex:

• I sell for 100,000 euros in year 1

• Sales go up to 120,000 in year 2

(120,000-100,000)/100,000 = 20,000/100,000 = 0.2 = 20%

• Sales have increased by 20%

Percentage variation from 100 to 120

Percentage to reflect the evolution of any given quantity

From 100 to 120

I sell for 100,000 euros in year 1

Sales go up to 120,000 in year 2

Percentage variation:

(difference between Final and orignialvalue)/original value

(120,000-100,000)/100,000 = 20,000/100,000 = 0.2 = 20%

• Sales have increased by 20%

Percentage variation from 140 to 175

Percentage to reflect the evolution of any givenquantity

From 100 to 120

From 140 to 175

Variation = 175-140 = 35 to be compared with the original value 140

• 35/140 = 0,25 = 25%

Salary variation— 30k example 

I earn 30,000 euros

At the end of the year my boss offers an increase of 500 euros

Percentage increase:

Variation / original value
500/30 000 = 0.016666 = 1,66%

Is that generous?

Sales variation

(ex:100k selling)

I sell for 100,000 euros in year 1

Sales go down to 90,000 in year 2

Variation = final value-original value = 90,000 – 100,000

-10,000 NEGATIVE also noted (10,000) betweenbrackets

Percentage variation

• Variation/original value = -10,000/100,000 = -0.1 = -10% = (10%)

Percentages higher than 100%

exhibit A:

exhibit B: 

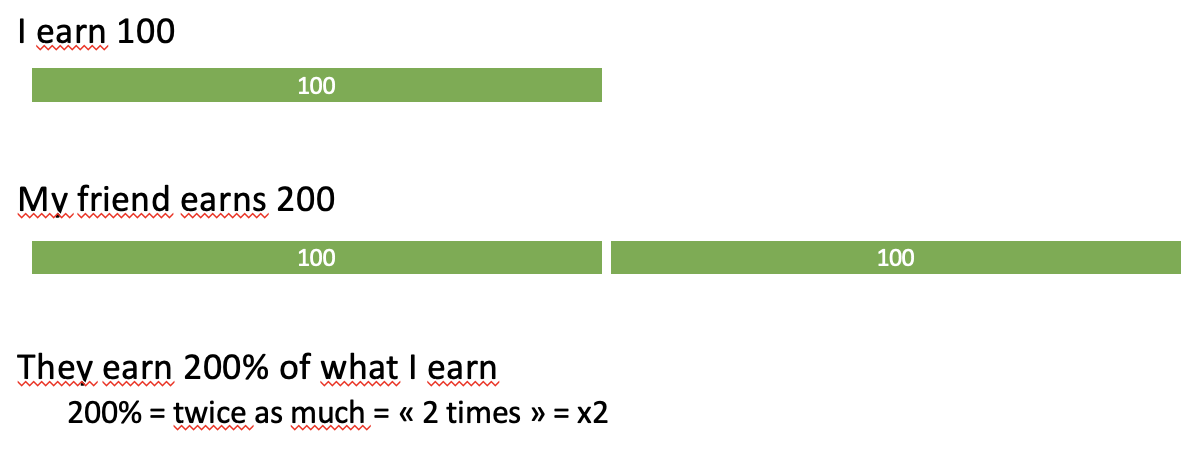
exhibit C:

Sales variations

• Growing on top of previous growth

• Compound Annual Growth Rate (CAGR)

• Growing on top of previous growth

• Compound Annual Growth Rate (CAGR)

  • (CAGR) measures the rate of return for an investment — such as a mutual fund or bond — over an investment period, such as 5 or 10 years.

  • (CAGR) is defined as the mean annual growth rate of a value over a specific time period, commonly expressed in percentage terms

Sales variation— example 1/ part.A

I sell for 100,000 euros in year 1

Sales increase by 20% in year 2 and another 20% in year 3

• Increase in year 2 = 20% of 100,000 = 0.2 x 100,000 = 20,000

  • —> Sales in year 2 reach 100,000 + 20,000 = 120,000

• Increase in year 3 = 20% of 120,000 = 0.2 of 120,000 = 24,000

NOTE 24,000 > 20,000

—> Sales in year 3 will be 144,000

Sales variation— example 1/ part.B

I sell for 100,000 euros in year 1

Steady increase of 20% each year

• Sales in year 2: 100,000 + 20,000 = 120,000

• Sales in year 3: 120,000 + 24,000 = 144,000

• Sales in year 4: 144,000 + (0.2*144,000) = 144,000 + 28,800 = 172.8

—> NOTE 172.8 > 144 > 120…

Stable in percentage… Acceleration in absoluteincreases

Steady increase of 20% each year…

• Increase in year 2: 20,000

• Increase in year 3: 24,000

• Increase in year 4: 28,800

Stable in percentage… Acceleration in absoluteamounts of the increases

COMPOUND GROWTH (Cumulated)

What is a loan ?

A loan is a financial arrangement in which a lender provides funds to a borrower. In this arrangement, the borrower must repay the borrowed amount along with interest over a set period of time.

• A loan is a sum of money that one or more individuals or companies borrow from banks or other financial institutions so as to financially manage planned or unplanned events. In doing so, the borrower incurs a debt, which he has to pay back with interest and within a given period of time.

Interest rate

The interest rate is the amount a lender charges a borrower and is a percentage of the principal—the amount loaned

• If you are borrowing money, the interest rate (or lending rate) is the amount you are charged for doing so – shown as a percentage of the total amount of the loan. The higher the percentage, the more you must pay back.

Vs. Repayment/Instalment

• When you take out a mortgage, you'll need to decide how you're going to repay it. With an interest-only mortgage, your monthly payments only cover the interest charged on your loan. With a repayment mortgage, your monthly payments are also used to pay back the initial sum you borrowed.

What is the difference between interest rate and payment?

Interest rates are the cost of borrowing, shown as an annual percentage. They can be either fixed, meaning they stay the same, or variable, where they can change based on market conditions. Monthly payments, meanwhile, are determined by the loan amount, the interest rate, and the loan term

What is a loan – vocabulary and grammar

I lend you some money = you borrow some money from me

• Lending vs borrowing

• I grant you a loan = you get a loan from me

Loan – credit – bond – obligation – debt

I finance you with some debt = you have a debttowards me

Basic loan (1)

Phase 1 – the borrower draws the loan

Conditions for this loan

Interests are charged at a rate of 5%

Yearly repayment of 1/10th of the principal –fully reimbursed in 10years

What is a loan (2)

Phase 2 – end of year 1 – the borrower pays some interest charges and partly repays the loan

Conditions for this loan

• Interests are charged at a rate of 5%

• Yearly repayment of 1/10th of the principal – fully reimbursed in 10 years

Basic loan (3)

Yearly transactions

• Interests are charged at a rate of 5%

• Repayment of 1/10th of the principal

Phase 3 – end of year 2 – what are the flows?

Basic loan (4)

Yearly transactions

• Interests are charged at a rate of 5%

• Repayment of 1/10th of the principal

Phase 3 – end of year 2 – the borrower pays someinterest charges and partly repays the loan

Basic loan (5)

Phase 11 – end of year 10 – the borrower pays someinterest charges and partly repays the loan.

The loan has been fully repayed.

What is a loan

A contract > room for negotiation

• Some prepackaged formats for individuals and SMEs

• Differences between countries

Largely flexible for corporates

Why do interest rates exist?— 4 reasons

• The compensation of expected inflation

• The cost of availability

• The cost of risk

• The administrative cost

Inflation— definition

Inflation is the decline of purchasing power of money (economists would say « a given currency ») over time. 

• Purchasing power is the value of money (a currency) expressed in terms of the volume of goods or services that one unit of money can buy.

It can weaken over time due to inflation. That'sbecause rising prices effectively decrease the number of goods or services you can buy. 

Inflation— what it looks like

The cost of availability (1)

I am going to hire you but I am not going to payyour salary at the end of the first month…

Do you accept? What are the limits?

What do you ask for in compensation?

The cost of risk (1)

I am setting up this new business and the new company is going to hire you but it cannot pay youfor the first six months, because it will only make cash later…

Technically it is a loan:

• The recruiter is asking you to grant a loan to your employer: it will owe you money for 6 months

The cost of risk (2)

I am setting up this new business and it is going to hire you but it cannot pay you for the first six months, because it will only make cash later…

• Technically it is a loan.

• It makes a difference to be paid in 6 months than in a couple of months…

• Availability cost and… risk that the borrower can’trepay the loan!

The cost of risk (3)

The cost of risk is the cost of incurring losses.

Figuring out this risk

• How likely is the loss likely

• How acceptable is the loss:

• an employee not being paid <> a bank not being paid

Note – vocabulary

• To default = being unable to meet the commitments as a borrower

• A default = failed payment of principal or of interests

The administrative cost

• Bank infrastructure to produce and market loans

• Bank’s profit requirements

Compound interests - definition

Compound interest is interest calculated on the initial principal, which also includes all of the accumulated interest from previous periods on a deposit or loan.

Compound interests – example calculation (1)

Bullet Loan

• Interest and principal are paid back at the end in one instalment (one shot)

Assumptions

• Initial amount borrowed 100 euros

• 10pc yearly interest rate (capitalised)

Compound interests – example calculation (2)

• End of year 1: 100 borrowed bearing 10 of interest: 110 due

• End of year 2: 110 borrowed bearing 11 of interest: 121 due

• End of year 3: 121 borrowed bearing 12.1 of interest: 133.1 due

• End of year 4: 133.1 borrowed bearing 13.3 of interest: 144.4 due

Compound interests on 100 of borrowing are 44.4

→ not 4x10=40

Compound interests – examplecalculation (3)

Bullet loan of 100 (principal = P) bearing interest rate of 8pc per year

Amount borrowed

Compound interests - calculation

From compound interests to future value

Assume the current value of a product is 100 and yearly price inflation is on average 8pc per annum for the next 10 years.

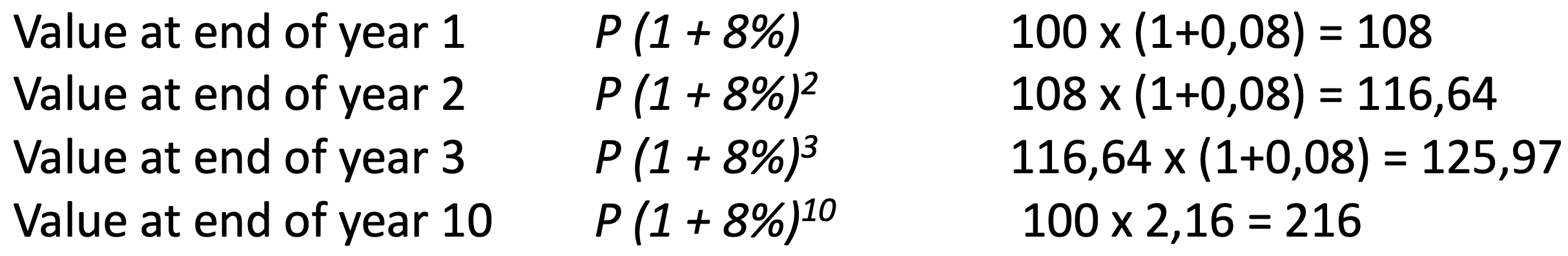
Future value

• (in 10 years with constant 8% inflation/interest vs current value of 100) is 216

Future value – calculation

Future value (FV) = the value of a current asset at a future date based on an assumed rate of growth

FV = PV (1 + i)ⁿ

Where:

• PV = present value

• i = growth rate in percentage terms

• n = number of compounding periods

Present value vs Future value

Present or current value (PV)

FV = PV (1 + i)ⁿ  >>    PV = FV/(1 + i)ⁿ

where:

• FV=Future Value

• i = Growth rate

• n = Number of periods​

Present and future value – CAGR

Trade media example

WWD

BoF

Vogue Business

+ international print press: Financial Times, NY Times, The Cut (NY Mag)…

(unfortunately Continental European ones, Le Monde, Les Échos, Italians etc not in the sameleague – business model issues)

Interest rates— Case study: Should George buy or rent?

Buy or rent a flat?

• George is a successful advertising exec previously based in London who accepts a new job in Paris.

• He is French and wonders if he should buy or rent the flat he needs for his family (partner plus one kid), that is a two-bedroom flat between 60 and 90 square meters. He has limited savings, approx. 100 k euros.

George Case: information on the market

• A good quality flat in central Paris sells for between 11 000 and 16 000 euros per square meter

• A good quality two-bedroom flat in central Paris is rented out for between 2200 and 3200 euros a month

• The transactional tax for real-estate buyers is 7%.

• The yearly real-estate tax for real-estate owners is 0,5%.

• Interest rates for deposits are zero and for 10-year borrowings 3.5% including insurance

Should George invest in a flat?

• Flat between 60 and 90 square meters

• George’s savings 100 k euros

• Sales value: 11 000 and 16 000 euros per square meter

• Rent value: 2200 and 3200 euros a month

• Transactional tax for real-estate buyers = 7%

• Yearly real-estate tax for real-estate owners = 0,5%

• Interest rate for deposits = zero

• Interest rate for 10-year borrowings = 3.5%

Performance in numbers (2)

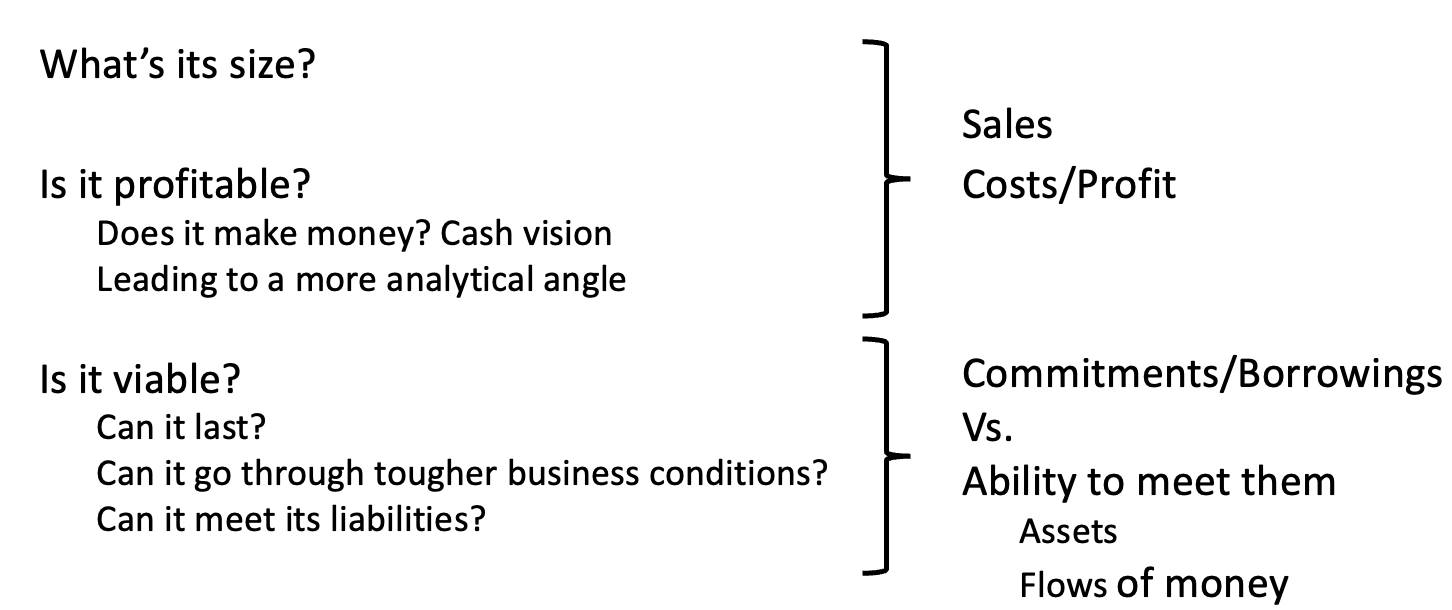
Information in the financial statements

• Sales / Costs / Results (Profit/Loss)

• Financings

  • from the investors and the lenders

 

• Use of the financings

  • investments by the company

  • NB use of word to invest/investments

• Cash flows / Cash in bank

Financial statements

How are financial statements divided

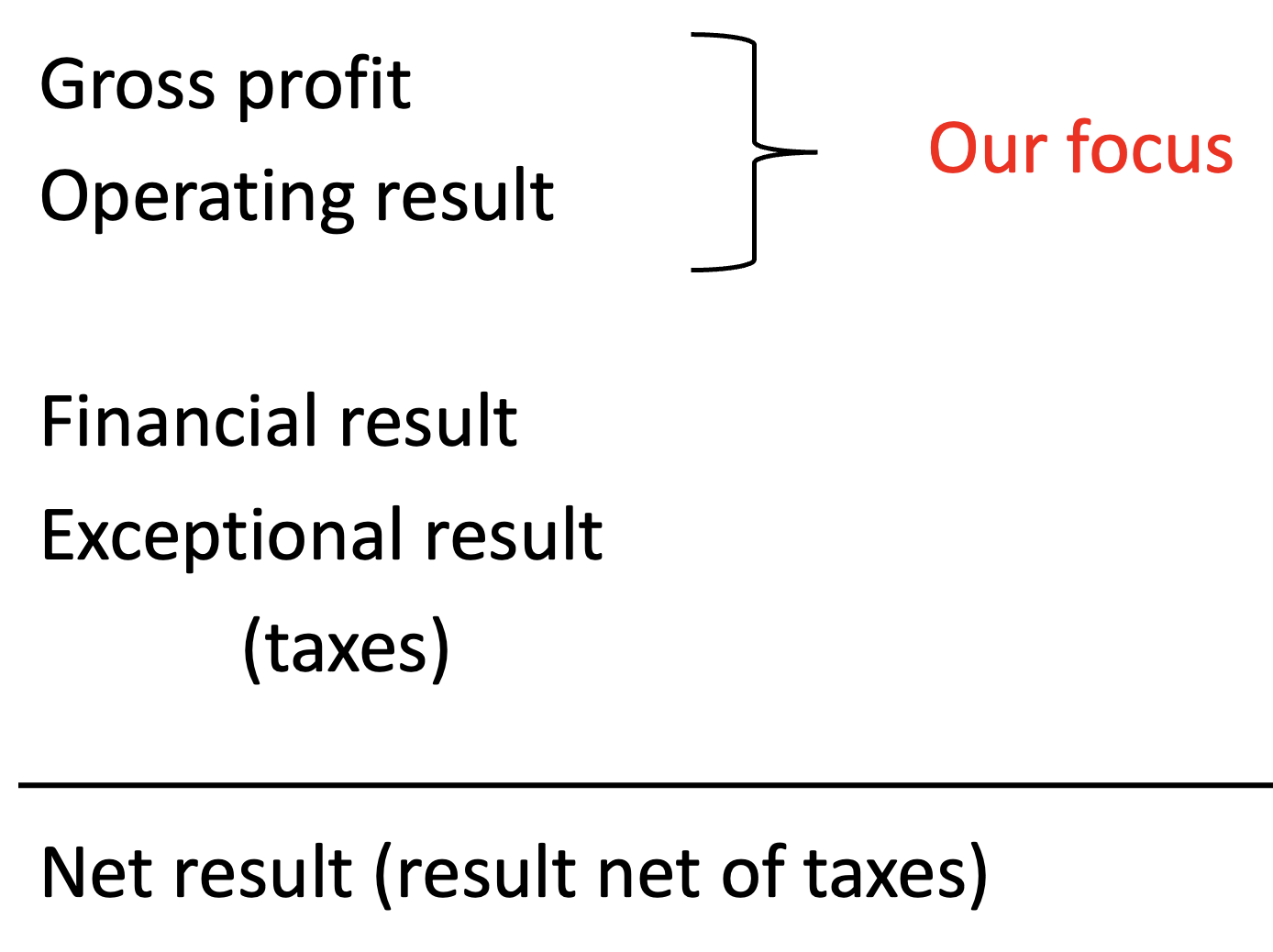
P&L— build up

P&L – build up: operating side

• Revenues  Sales in relation to the business

• (costs)  Costs necessary to conduct the business = Operating costs

• Result/profit  Operating result 

P&L – build up: beyond the operations

Operating result

• Revenues  —> Sales in relation to the business

• (costs) —> Operating costs

• Result/profit  —> Operating result

Non operating revenues and costs

• Financial revenues and costs

• Exceptional items

• Taxes on profits

P&L – build up (cont’d)

P&L – more scrutiny on operating performance

Looking into 2 types of operating costs 

P&L – detailed operating performance

• Revenues  —> Sales in relation to the business

• (costs of good sold - COGS) —> costs necessary to the acquisition and   production of goods or services sold

• Result/profit  —> Gross profit

• (Selling General and Admin. —>  costs necessary to the selling and SG&A)  marketing of goods or services sold

• Result/profit —> Operating profit

P&L – Full P&L

P&L – what does it look like: public information + listed companies who volunteer

ex:

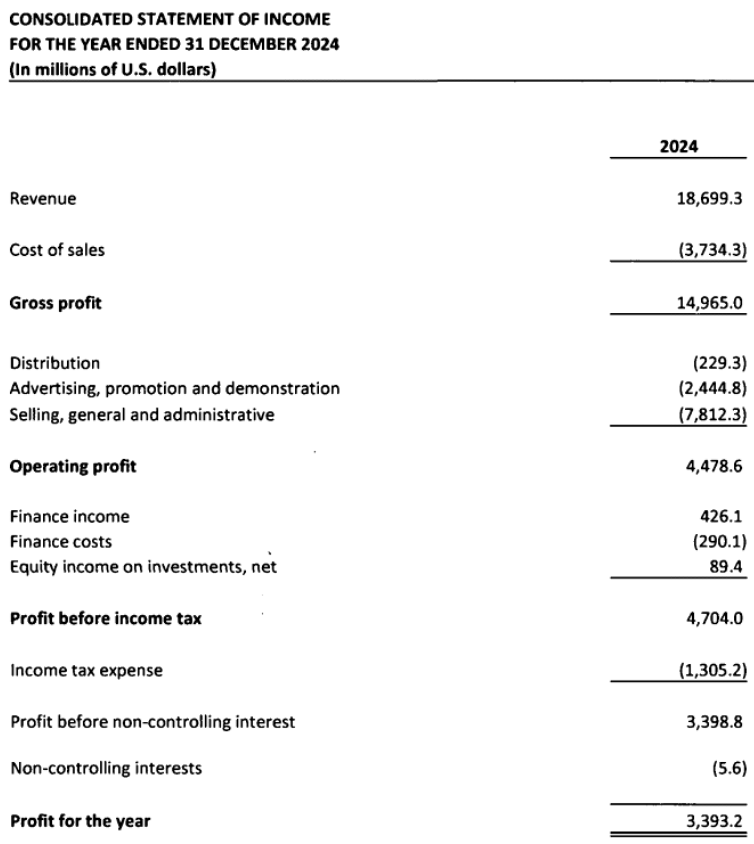
Purpose of a P&L

Comprehensive view of the profitability of doing business

Exhaustive coverage of revenues/gains and of costs/losses

• Revenues which are certain but not materialised yet

• Costs incurred but not paid yet

• Costs in relation to investments made by the company which are used and losing value

P&L – Costs incurred but not paid yet

• Bonuses

• Pension planning

P&L – Use of assets

Assets needed for production/distribution/administration… whenbought are accounted for as assets in a separatestatement (balance sheet)

—> Their use is progressively accounted for… it is a cost affecting the P&L

• It’s reflecting the depreciation of those assets as they ageand progressively lose their interest (wear and tear)

• It’s a non cash cost

P&L – synonyms

• Profit and loss account

• Statement of income / income statement

• Statement of earnings / earnings statement / earnings report