Geometric Applications of Binary Search Trees

Geometric Applications of Binary Search Trees

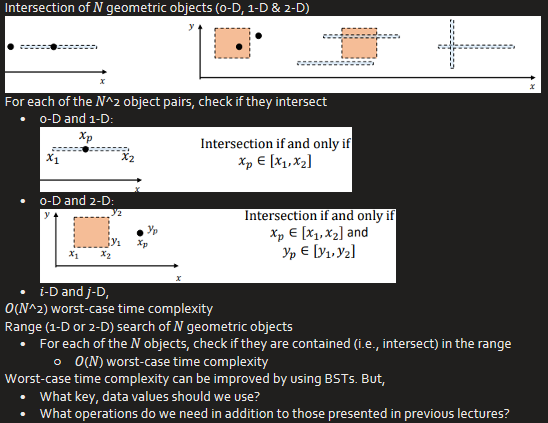
Intersection of geometric objects in 1 and 2 dimensional spaces

Intersection of Geometric Objects

• Orthogonal Line Segment and Rectangle Intersection

• 1-D & 2-D Range Search, 1-D Interval Search

Orthogonal Line Segment and Rectangle Intersection

Computer Assisted Design (CAD), and CAD for Very Large Scale Integration (VLSI)

• For example, designing electronic chip can require:

• Wires must not intersect

• Wires must have some minimum distance between them

CAD design software helps with checking that

1-D & 2-D Range Search, 1-D Interval Search

Naïve Solutions

1-Dimension Range Search

Use a Dictionary ADT extension:

• void insert(Key key, Value value)

• Value Search(Key k)

• void delete(Key k)

• List rangeSearch(Key keyLeft, Key keyRight) 

• int rangeCount(Key keyLeft, Key keyRight)

More generally (beyond just geometric search), rangeSearch and rangeCount can be used for database queries

1-Dimension Range Search Worst Case Time Complexity

• rangeCount: 𝑶(𝐥og 𝒏) time

  • Operation rank() takes 𝑂(log 𝑛) time

  • rangeCount uses rank() twice (four times in code)

• rangeSearch: 𝑶(𝑹 + 𝐥og 𝒏) time, where 𝑹 is the number of keys contained in range

  • Time is a factor of the search path to low key value, as well as to the search path to high key value

  • And finally factor of all keys in range

• Compare to the naïve solution with 𝑂(𝑛) worst-case time complexity

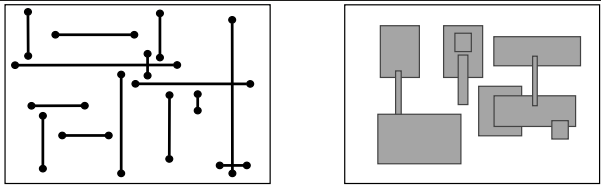
Orthogonal Line Segment Intersection

Given 𝑁 line segments (either horizontal or vertical), find all intersections

Non-degenerate segments: all 𝑥 and 𝑦 coordinates are different

2D problem seems hard, but we have just solved a 1-D problem: 1-D Range Search

• Can we reduce our 2-D problem to the 1-D range search?

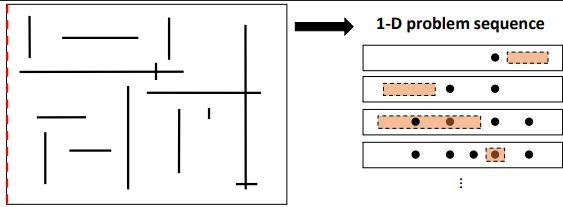
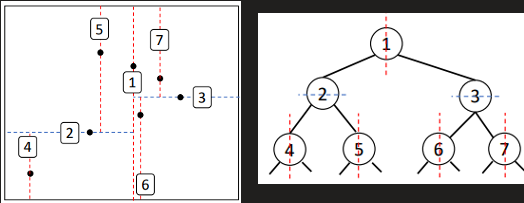
  • Sweep-Line Algorithm

• Transform 2-D problem into a sequence of 1-D range search problem instances

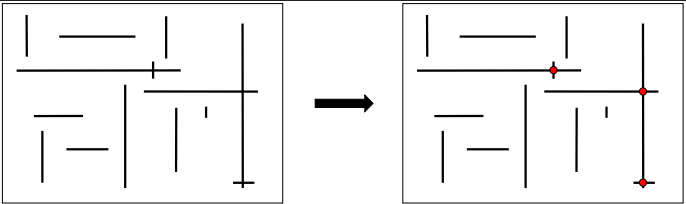
Sweep-Line Algorithm

• Create a BST

• Insert key 𝑦1

• Range search (𝑎1, 𝑎2)

• Insert key 𝑦2

• Range search (𝑏1, 𝑏2)

• Insert key 𝑦3

• Insert key 𝑦4

• Insert key 𝑦5 

• rangeSearch(𝑐1, 𝑐2)

• Remove key 𝑦1

• …

Common technique for solving geometrical problems:

• Convex hull,

• Convex object intersection,

• Voronoi diagrams …

The concept is also used for generating slices in additive 3D printing

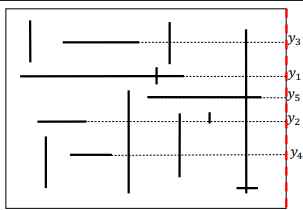
Transforming 2-D problem into a sequence of 1-D range search problem instances

• At most:

  • N rangeSearch,

  • N insertions,

  • N deletions

• Thus it takes time 𝑂(𝑁 log 𝑁 + 𝑅), for R intersections

• Worst-case time complexity of intersection: 𝑂(𝑁 log 𝑁 + 𝑅), when there are 𝑅 intersections

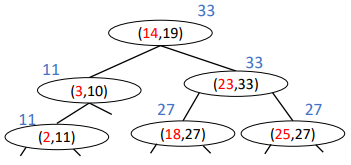
Interval Search Tree

Operations:

void insert(Key low, Key high, Value value)
Value search(Key low, Key high)
void delete(Key low, Key high)
LinkedList intersects(Key low, Key high)

left endpoint is the BST key

And nodes store max endpoint in subtree (rooted at the node)

Non-degenerate intervals: no two intervals have the same left endpoint

Insertion - Interval Search Tree

void insert(Key low, Key high, Value value)

• Insert the new node using low as the BST key

• Update max in each node on the search path

insert(26,40, *)

Intersection - Interval Search Tree

Value intersectionSingle(Key low, Key high):

• If interval in node intersects (low,high)-interval, return that interval

• Else if left child (and subtree) is null, recurse on right child,

• Else if max endpoint of left child (i.e., in left subtree) < low, recurse on right

• Else recurse on left subtree

intersectionSingle(20,21)

Intersection Analysis - Interval Search Tree

Proof sketch:

• If recurse right, there are no intervals in left subtree that recurse

  • Max (in left subtree) < low 

  • For any interval (a,b) in left subtree, 𝑏 ≤ max < 𝑙ow

  • Thus for any interval (a,b) in left subtree, (a,b) does not intersect (low,high)

• If recurse left, there is either an intersection in the left subtree or no intersection on either subtree

  • Recursing on left implies 𝑙ow ≤ 𝑚ax (for max in left subtree)

  • If no intersection on left subtree, then (c, max) does not intersect (low,high), i.e., ℎ𝑖gh < 𝑐

  • Since we have a BST ordered by intervals’ left endpoints, for any interval (a,b), 𝑐 ≤ 𝑎

  • Thus ℎ𝑖gh < 𝑐 ≤ 𝑎, and there are no intersections on the right subtree

Worst-case Time Complexity of intersectionSingle: 𝑂(log 𝑁)

Worst-case Time Complexity of intersection: 𝑂(𝑅 log 𝑁)

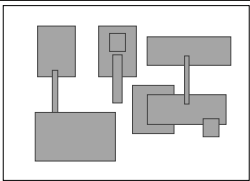
Orthogonal Rectangle Insertion

• Find all intersections among a set of 𝑁 orthogonal rectangles

• Non-degenerate: All 𝑥 and 𝑦 coordinates are distance

• To avoid naïve 𝑂(𝑁^2) time solution, transform/reduce orthogonal rectangle insertion to 1D interval search problem instances

  • Use Sweep-line algorithm

• Interval searches when there are 𝑅 intersections: 𝑂(𝑁 + 𝑅 log 𝑛) worst-case time complexity

• Compared to orthogonal line segment intersection -> extra complexity due to the interval search tree implementation

2-Dimension Range Search

Problem definition:

• Given 𝑁 points on 2D space, and a 2D range (here, an axis-aligned rectangle), output the points contained in the range

• (Count version): … output the number of points contained in the range

Extend the Dictionary ADT to 2D keys:

• Insert a 2D key

• Delete a 2D key

• Search for a 2D key

• rangeSearch: find all keys that lie in a 2D range

• rangeCount: number of keys that lie in a 2D range

For our use, Keys are points in the plane and we want to find/count points in a given axis-aligned rectangle

Grids

Extend Dictionary ADT to 2D keys via a grid implementation (array analogue):

• Divide space into an M-by-M grid (i.e., decide on grid “granularity”)

• Create list of points contained in each square

• Use 2D array to directly index each square

• Insert(x,y): add (x,y) to list for corresponding square

• rangeSearch: examine only squares that intersect 2D range query

• To compute intersecting squares - Use top right and bottom left points defining the range query

Space: 𝑀^2 + 𝑁

Time: 1 + 𝑁/𝑀^2 per square examined, on average

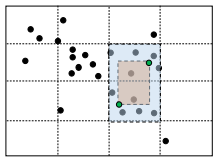
Grid Square Size impacts Performance

Small size (bigger 𝑀^2) wastes space

Large size means you have many points per square (on average)

Good tradeoff: √𝑁 x √𝑁 grid

• For √𝑁 x √𝑁 grid, if points are evenly distributed, then:

  • Initializing the data structure takes N space 

  • Inserting a point takes 𝑂(1) time

  • Range Search also takes 𝑂(1) time because 1 point per square

Space-Partitioning Trees

Rather than dividing the space evenly into squares, you can divide in several other ways:

• Into two half spaces (not necessarily even sized)

• Into four squares (even sized)

• Into two regions

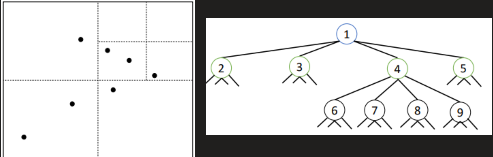
2D Tree Construction

Recursively partition plane into two halfplanes

• Even level points partition in two subsets: to their left, and to their right, respectively

• Odd level points partition in two subsets: below them, and above them, respectively

2D Tree Construction Analysis

• Space: Θ(𝑁)

• Worst case Time: 𝑂(𝑁 log 𝑁)

2D Tree Range Search

Find all points in a query axis-aligned rectangle:

• Check if root point is in the query rectangle

• Check left/bottom recursively (if rectangle extends into that part)

• Check right/above recursively (if rectangle extends into that part)

2D Tree Range Search Analysis

• Average (Expected) case: 𝑂(𝑅 + log 𝑁) time

• Worst case: 𝑂(𝑅 + 𝑁) time

2D Tree Nearest Neighbour

Find closest point to query point

• Check distance from point 1 to query point

• If left/bottom could contain a closer point, recurse left

• If right/top could contain a closer point, recurse right

Output current closest point to query point

2D Tree Nearest Neighbour Analysis

• Average (Expected) case: 𝑂(log 𝑁) time

• Worst case: 𝑂(𝑁) time

KD Trees

Extension of 2D trees to more dimensions is widely used

• Good for high-dimensional and clustered data

• Can be used for N-body simulation (physics)

3D tree example:

• 𝑥-dim

• 𝑦-dim

• 𝑧-dim

Quadtree Construction

Recursively partition plane into four squares

• Each square holds up to some 𝑘 = 2 points,

• Any square that has more points is split up into four sub squares

• Tree structure follows the partition structure

In quadtrees, regular partition that adapts to point density

Can be used on images, and pixels take the “role of points”

• Compression of images

• Check connected components in image (image processing)

Replacing BSTs with Skip Lists

• Probabilistic data structures

• Another way to implement Dictionary ADT with fast insertion, deletion and lookup

• Main idea: Multiple layers of linked lists over 16 elements

Contains log_1/p (𝑛) lists:

• Layer 1: Bottom layer & a simple linked list (here, over 16 elements)

• Layer 2: Each element of layer 1 is in layer 2 with probability 𝑝 (here, 𝑝 = 1/4 )

• Layer 3: Each element of layer 2 is in layer 3 with probability 𝑝

Replacing BSTs with Skip Lists Advantages

Simple to implement and efficient on average

• Average case complexity: 𝑂(log 𝑛 )

• Worst-case complexity: 𝑂(𝑛)

• Space complexity: 𝑂(𝑛 log 𝑛)

In practice, skips lists are used:

• MemSQL

• Discord

• RocksDB

• …

Good for concurrency, and in that context, has been a research focus

• Concurrent? For example, when multiple threads access same data structure