Mechanics and materials

Scalar

Scalar quantities only have a magnitude (size)

• Distance: the total length between two points

• Speed: the total distance travelled per unit of tim

Vector

• Vector quantities have both magnitude and direction

  • Displacement: the distance of an object from a fixed point in a specified direction

  • Velocity: the rate of change of displacement of an object

  • Acceleration: the rate of change of velocity of an object

What are the SUVAT Equations?

V = U+ AT

S = ½ (V+U) x T

V² = U² +2AS

S = UT + ½ AT²

S = VT - ½ AT²

How can light gates be used to investigate acceleration down a ramp?

• A trolley with a card attached is released from the top of a ramp.

• Two light gates (connected to a computer) are positioned at different points along the ramp.

• As the trolley moves, the card interrupts the light beams, allowing the computer to measure time and speed at each gate.

• Using the equation v = u + at, acceleration (a) can be calculated.

• Load

Acceleration due to free fall

The acceleration of any object in response to the gravitational attraction between the Earth and the object

g = 9.81

What is a common experimental method to determine the acceleration due to gravity (g)?

• Use a free-fall apparatus where a ball is dropped from a known height.​

• Employ a timer or light gate to measure the time taken for the ball to fall.​

• Apply the kinematic equation: s = ut + 0.5gt², where s is the distance fallen, u is initial velocity (0 m/s), t is time, and g is acceleration due to gravity.​

• Rearrange to solve for g: g = 2s / t².

What equipment is used to measure acceleration due to gravity in a free-fall experiment, and what is

• Meter ruler: Measures the distance between the light gates.

• Steel ball-bearing: Acts as the falling object; must be magnetic (iron/steel).

• Electromagnet: Holds and releases the ball without applying force.

• Two light gates: Measure the time taken for the ball to fall.

• Timer: Records the time the ball takes to pass between the light gates.

• Tall clamp stand: Holds the electromagnet and light gates in position.

• Cushion: Prevents damage to the ball or surface upon impact.

Define Thinking and Braking Distance

The distance a vehicle travels while the driver reacts to a hazard before applying the brakes. It depends on:

• Reaction time (influenced by tiredness, distractions, alcohol, etc.).

• Speed of the vehicle (higher speed = greater thinking distance).

Braking Distance:

The distance the vehicle travels after the brakes are applied until it comes to a complete stop. It depends on:

• Speed (higher speed = longer braking distance).

• Road conditions (wet/icy roads increase braking distance).

• Brake and tire condition (worn-out brakes/tires reduce effectiveness).

• Mass of the vehicle (heavier vehicles take longer to stop).

Define stopping distance and its formula

Stopping Distance:

The total distance a vehicle travels from the moment a driver sees a hazard until the vehicle comes to a complete stop.

Formula: Stopping Distance=Thinking Distance+Braking Distance\text{Stopping Distance} = \text{Thinking Distance} + \text{Braking Distance}Stopping Distance=Thinking Distance+Braking Distance

What are the two independent components of projectile motion, and how do they behave?​

• Horizontal Component: Constant velocity due to no acceleration (assuming air resistance is negligible).​

• Vertical Component: Uniform acceleration due to gravity, causing the object to decelerate upwards and accelerate downwards.

How does velocity change while in motion?

Horizontal velocity stays constant

Vertical velocity can differ if going downwards the value can increase if acting upwards it will decrease as it acting against gravity

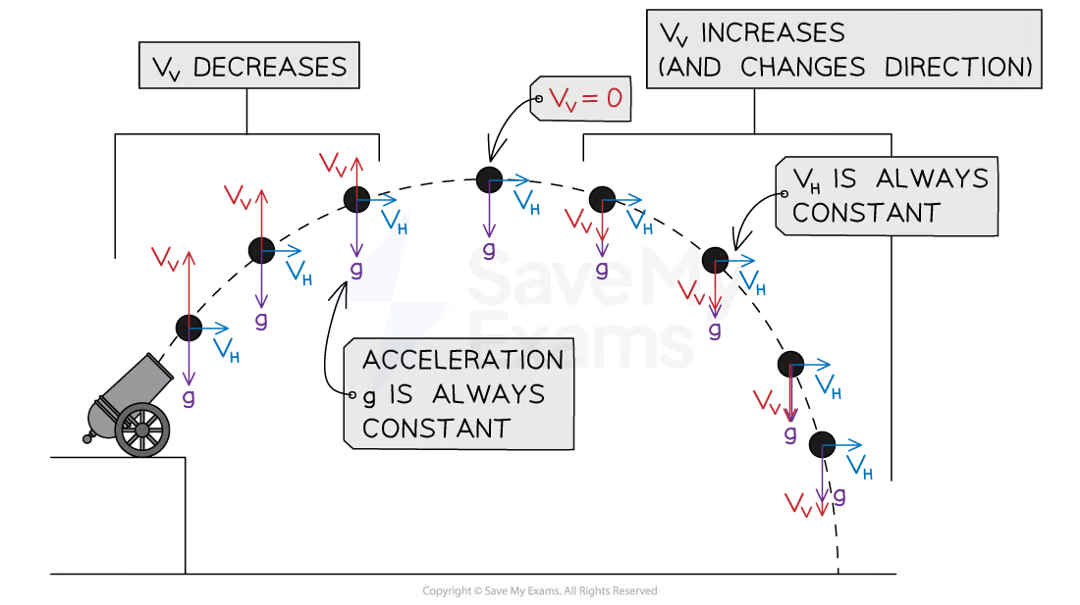
Define the following terms related to projectile motion: Time of Flight, Maximum Height, and Range.​

• Time of Flight: The total time the projectile remains in the air.​

• Maximum Height: The peak vertical position reached by the projectile.

• Range: The horizontal distance traveled by the projectile from launch to landing.​

How can you find Time of Flight, Maximum Height and Rang e

Application of SUVAT EQUATIONS

The formula for Resultant Force

F = M x A

Resultant Force (N) = Mass (KG) x Acceleration m/s²

An unbalanced force on a body means it experiences a resultant force

What is weight and how do you calculate it

• Weight is the effect of a gravitational field on a mass

  W = MG

• Weight (Newtons) = Mass (Kg) x Acceleration due to Gravity (N/Kg)

Define tension

• The force experienced by a cable, rope, or string when pulled, hung, rotated or supported

Define Normal Contact Force/Reaction force

The force arising when an object rests against another object acting at a 90° angle to the plane of contact

Upthrust:

The upward buoyancy force acting on an object when it is in a fluid

Upthrust can occur in liquids and gases

Friction:

• The force that arises when two surfaces are in contact with each other

• Friction always opposes the motion

What is the purpose of a free-body diagram?​

To represent all the forces acting on a single object, illustrating both the magnitude and direction of each force

What is drag forces

• Drag forces are forces that oppose the motion of an object moving through a fluid (gas or liquid)

• friction and air resistance

What is lift?

Lift is an upwards force on an object moving through a fluid. It is perpendicular to the fluid flow

Factors affecting Drag

• The speed of the object

• The object’s shape and texture

• The density of the fluid

Factors affecting air resistance

• Cross-sectional area

• Shape

• Altitude

• Temperature

• Humidity

What is terminal velocity

• When the drag force is equal to the gravitational pull on the body, the body will no longer accelerate and will fall at a constant velocity

• This velocity is called the terminal velocity

What is a moment and formula

The turning effect of a force occur when forces cause objects to rotate about some pivot.

Moment (N m) = Force (N) × perpendicular distance from the pivot (m)

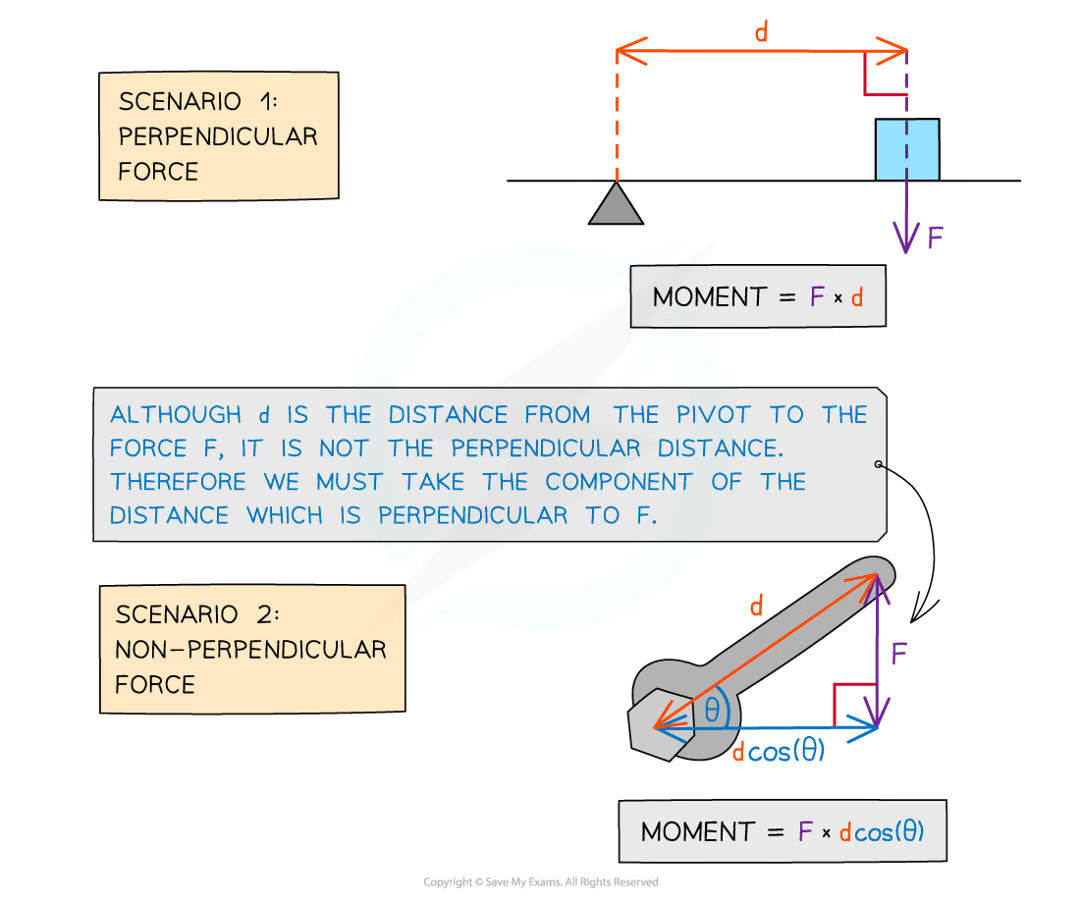
What is the principle of Moments

For a system to be in equilibrium, the sum of clockwise moments about a point must be equal to the sum of the anticlockwise moments (about the same point)

What is a couple

A couple is a pair of equal and opposite coplanar forces that acts to produce rotation only

Equal in magnitude

Opposite in direction

Perpendicular to the distance between them

What is torque and how do i calculate

The moment of a couple is known as a torque

The torque of a couple can be calculated with the following equation:

T = Fd

• τ = torque (N m)

• F = one of the forces (N)

• d = perpendicular distance between the forces (m)

What is a centre of mass and when base is changed hpw dpes the centre of mass

an object is the point at which the weight of the object may be considered to act

wider base an object has, the lower its centre of mass and it is more stable

narrower base an object has, the higher its centre of mass and the object is more likely to topple over if pushed

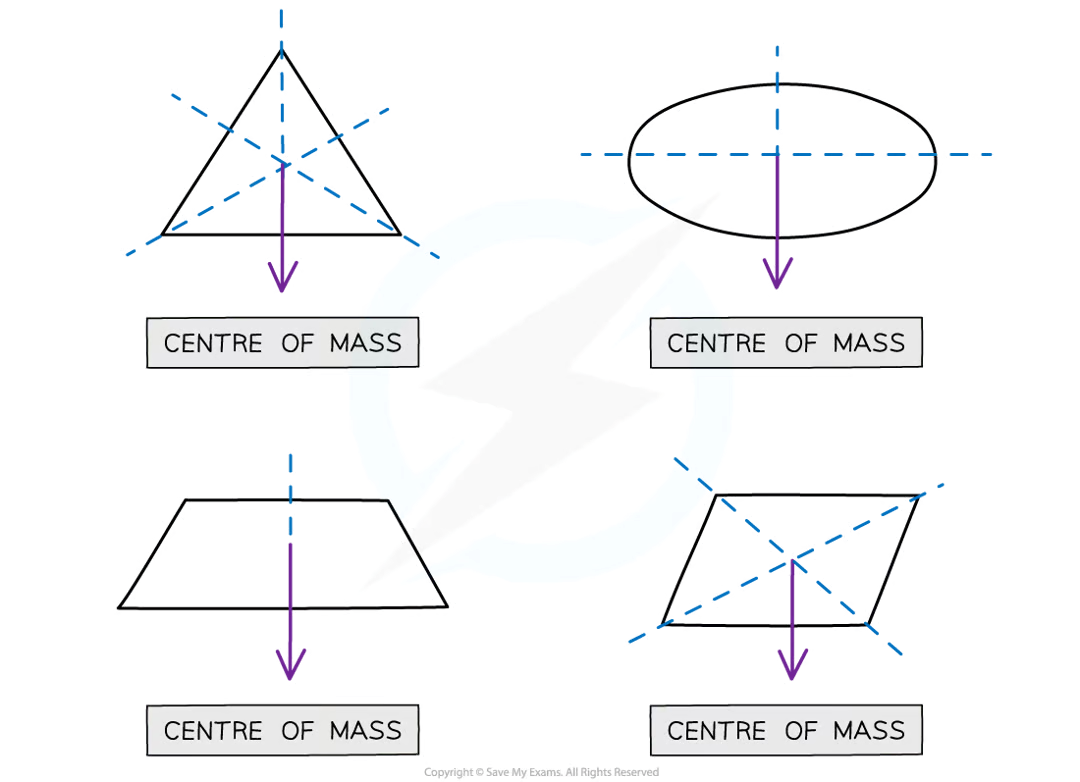
How can you determine the centre of mass of an irregular shape experimentally?

• Suspend the irregular shape (plane lamina) from a pivot and allow it to settle.

• Hang a plumb line from the pivot and draw a vertical line along its path.

• Repeat the process from two or three different pivot points, drawing a vertical line each time.

• The centre of mass is located at the point where all the lines intersect.

What is equilibrium

• A system is in equilibrium when all the forces are balanced. This means:

  • There is no resultant force

  • There is no resultant torque

Conditions for Equilibrium

• Coplanar forces can be represented by vector triangles

• Forces are in equilibrium if an object is either

  • At rest

  • Moving at constant velocity

  • A closed vector triangle represents a object in equilibrium

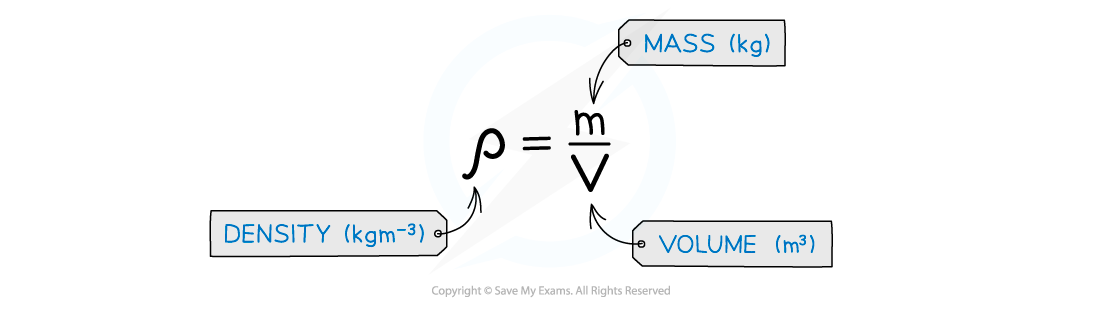
What is density and it’s formula

Density is the mass per unit volume of an object.

P (Density kg/m³) = m (Mass kg)/Volume(m³)Density is the mass per unit volume of an object

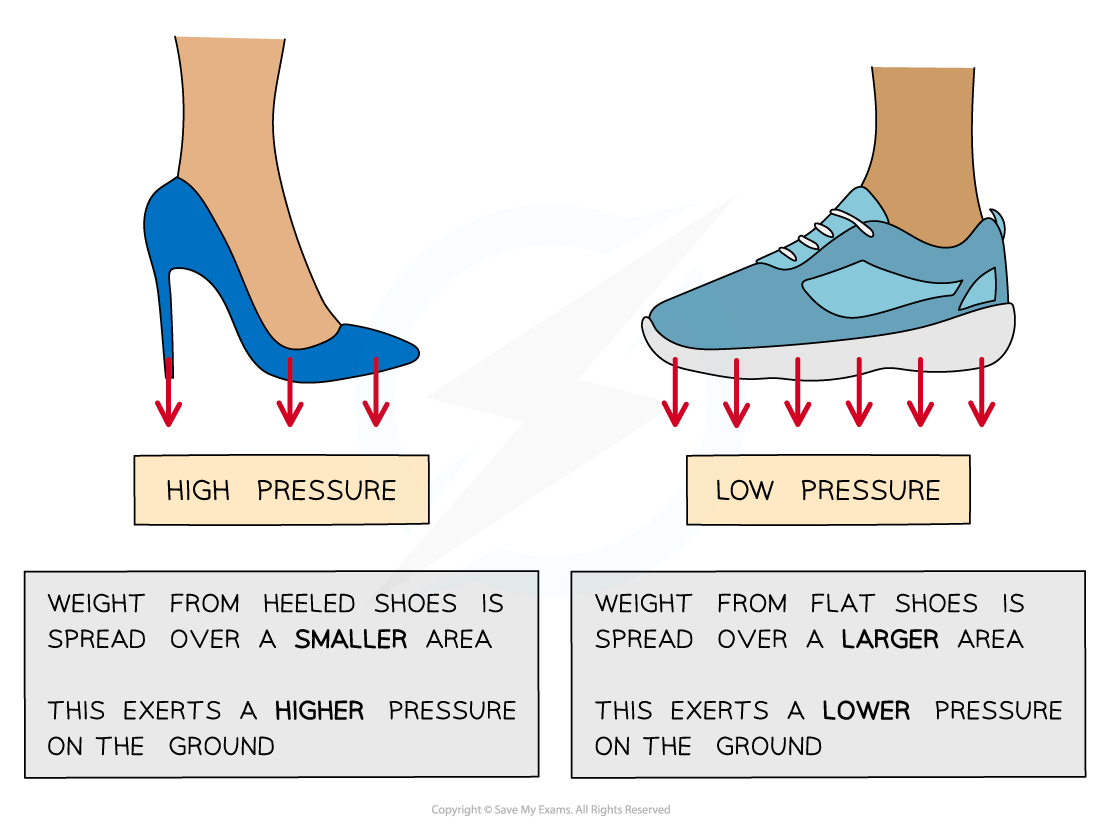
What is pressure and what is its formula

how concentrated a force is, it is defined as the force per unit area

How does area affect pressure

• If a force is spread over a large area it will result in a small pressure

• If it is spread over a small area it will result in a large pressure

Newton’s First Law

An object will remain at rest or move with constant velocity unless acted on by a resultant force (all forces are balenced)

An object will remain at rest or at constant acceleration unless

a resultant force acts upon it

Newtons Second Law

The resultant force acting on an object with a constant mass is directly proportional to its acceleration

F = ma

= resultant force, measured in newtons (N)

= mass of object, measured in kilograms (kg)

= acceleration, measured in metres per second squared (m s⁻²)

Resultant force affect on acceleration

• If the resultant force acts along the direction of the object's motion, the object will:

  Speed up (accelerate)

  Slow down (decelerate)

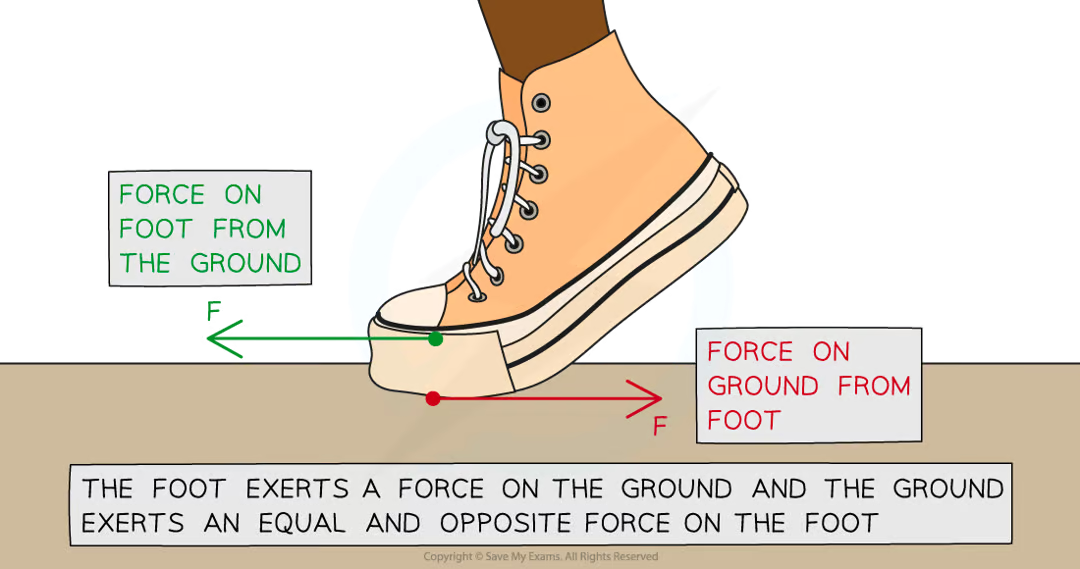
Newtons Third Law

If Object A exerts a force on Object B, then Object B will exert a force on Object A which is equal in magnitude but opposite in direction

What is linear momentum and how is it defined?

Linear momentum is the momentum of an object moving in only one dimension.
It is defined as the product of mass and velocity:
p = m × v

• p = momentum (kg·m/s)

• m = mass (kg)

• v = velocity (m/s)
  Momentum is a vector quantity — it has both magnitude and direction.

What happens to momentum if no external resultant force acts on a system?

The linear momentum of an object remains constant (is conserved)
unless acted upon by an external resultant force.
The initial direction of motion is usually assigned as the positive direction.

What is the principle of conservation of momentum?

The principle of conservation of momentum states that in a closed system, the total momentum before an event is equal to the total momentum after the event, provided no external forces act on the system. This can be expressed as:
Total momentum before = Total momentum after

What is meant by a "closed system" in the context of momentum conservation?

A closed system refers to a system where no external forces are acting, meaning the energy within the system remains constant. In such a system, momentum is conserved during interactions like collisions or explosions.

What happens to the total momentum when two objects move towards each other with equal speeds?

If two objects move towards each other with equal speeds, their momenta are equal in magnitude but opposite in direction. In a closed system, their total momentum sums to zero, demonstrating momentum conservation.

How is force related to momentum?

Force is defined as the rate of change of momentum on a body:
F = Δp / Δt
Where:

• F = force (N)

• Δp = change in momentum (kg·m/s)

• Δt = time interval (s)

How do you calculate the change in momentum?

Change in momentum = Final momentum − Initial momentum
This is used to find the net effect of a force acting over time.

What is the role of the resultant force in momentum change?

The resultant force is the net force responsible for changing an object’s momentum.
It's the force calculated using:
F = Δp / Δt

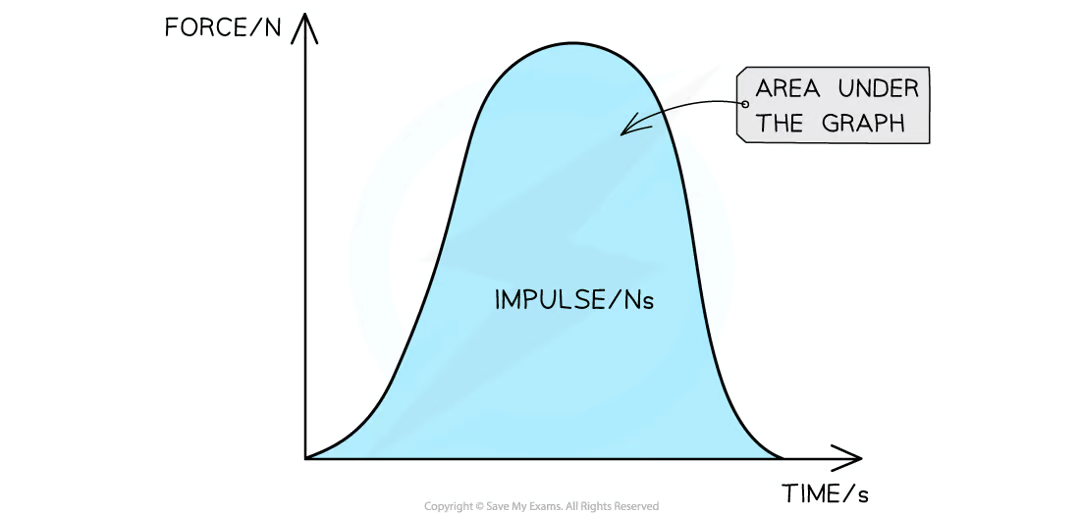
What is impulse

Impulse (N·s) = F × Δt

Vector quantity
It represents the change in momentum due to a force acting over time.

When can the impulse equations be used?

These equations are valid only when the force is constant over the time interval

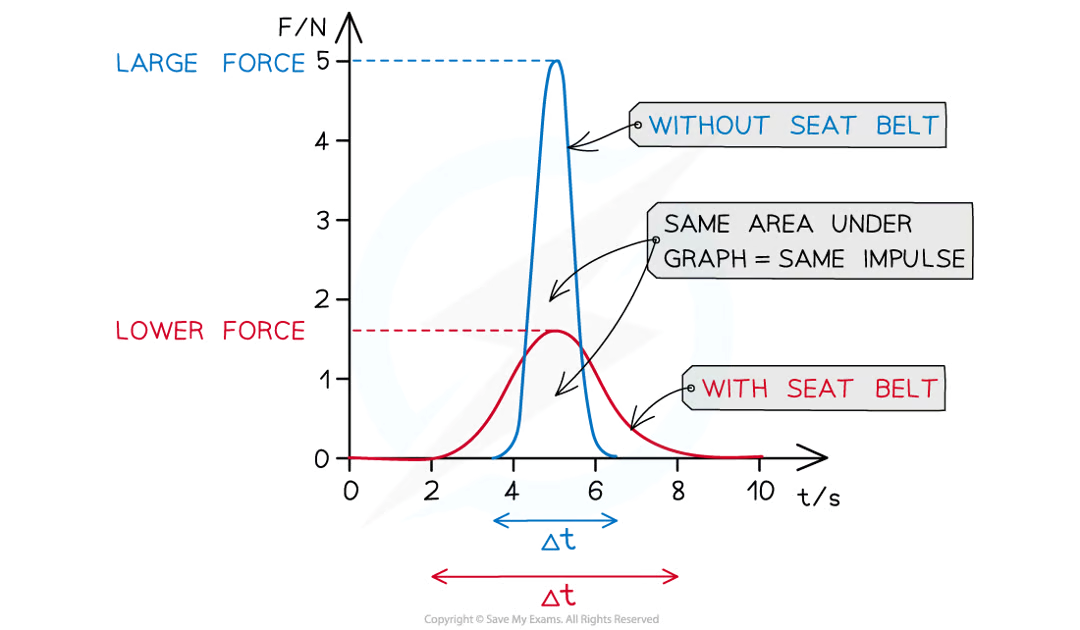
What does a Impulse graph look like? (force/time)

How do change the value of an impact force

by changing amount of contact time

What is the difference between elastic and inelastic collisions

Elastic collision:

Both momentum and kinetic energy are conserved

Total momentum before = Total momentum after

Total kinetic energy before = Total kinetic energy after

Inelastic collision:

Momentum is conserved, but kinetic energy is not

Total momentum before = Total momentum after

Total kinetic energy before ≠ after

Why are vehicle safety features designed to change shape during a collision?

They absorb energy and increase the time over which momentum changes to reduce the force on passengers during impact.

What is the purpose of seat belts in a collision?

Seat belts prevent passengers from hitting the vehicle interior and stretch slightly to increase contact time, reducing the force needed to stop the passenger's momentum.

How do airbags protect passengers during a crash?

Airbags act as a soft cushion, increasing the contact time during momentum change. This reduces the force on passengers when they're thrown forward in a collision.

What are crumple zones and how do they work?

Crumple zones are designed to crush in a controlled way during collisions, increasing the time over which the vehicle’s momentum changes, and thus reducing the force on passengers.

Compare large and small amounts of force on a graph in a collision

What is work done and how is it calculated?

Mechanical work is the energy transferred when a force causes an object to move over a distance.
If the force is constant and acts parallel to displacement, work done is:

W = F x s

W = work done (Joules)

F = force applied (Newtons)

s = displacement (meters)

1 N·m = 1 J (joule)

How do you calculate work done when the force is at an angle?

When a force acts at an angle (θ) to the direction of motion, only the component parallel to displacement does work.
The equation becomes:

W = F × s × cos(θ)

Where:

• W = work done (J)

• F = applied force (N)

• s = displacement (m)

• θ = angle between force and direction of motion (°)

  Use cos(θ) for horizontal work

  Use sin(θ) for vertical work

  Only the parallel component of the force contributes to work

What is power and how is it calculated in physics?

Power is the rate of doing work or the rate of energy transfer.

Formula 1:

P = ΔW / Δt
Where:

• P = power (watts, W)

• ΔW = work done (joules, J)

• Δt = time (seconds, s)

• P = F × v
  Where:

• F = force (N)

• v = velocity (m/s)

⚠ The force must be in the same direction as the velocity, or use the component of the force parallel to motion.

What does the area under Force-displacement represent

Work done

Define and show how to calculate efficiency

• The ratio of the useful power output from a system to its total power input

  Efficiency = useful power output/total power output x100%

The Principle of Conservation of Energy states that:

Energy cannot be created or destroyed, it can only be transferred from one form to another

What is energy dissipation and why is some energy considered "wasted"?

Energy dissipation refers to the loss of useful energy to the surroundings, usually as heat, light, or sound. No energy transfer is 100% efficient, so some energy is always wasted.

⚙ What are the formulas for kinetic energy and gravitational potential energy?

🔹 Kinetic Energy (KE):

KE = ½ × m × v²

• m = mass (kg)

• v = velocity (m/s)

🔹 Gravitational Potential Energy (GPE):

GPE = m × g × h

• m = mass (kg)

• g = gravitational field strength (9.8 m/s² on Earth)

• h = height (m)

What is Hooke’s Law and how is it expressed mathematically?

Hooke’s Law states that the extension of an elastic material is directly proportional to the applied force, up to the limit of proportionality.

🔹 Formula:

F = k × ΔL

• F = applied force (N)

• k = spring constant (N/m)

• ΔL = extension (m)

📈 This relationship is linear until the material’s elastic limit is reached.

What is the spring constant, and how does it relate to extension and compression?

The spring constant (k) measures the stiffness of a material.

• A larger k means a stiffer material.

🔹 Hooke’s Law applies to both:

• Extension: increase in length

• Compression: decrease in length

🔸 Extension (ΔL) is calculated by:

ΔL = Stretched length − Unstretched length

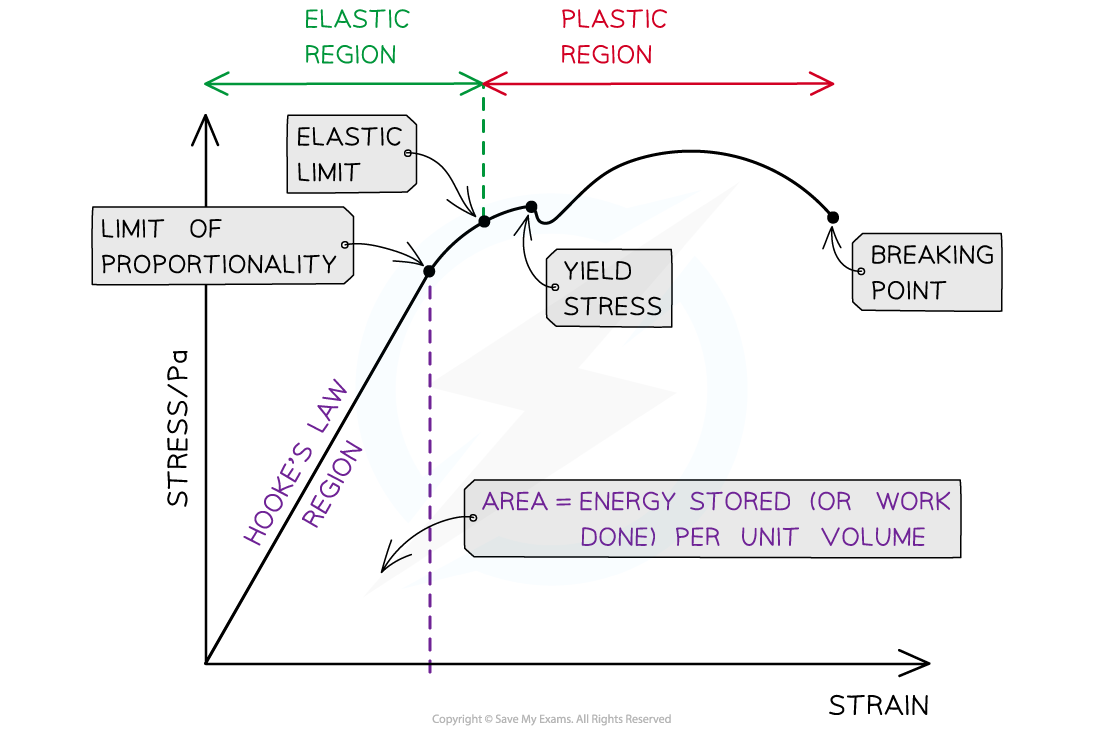
What does a force-extension graph show and what are its key features?

• Hooke’s Law Region:
  Straight line through the origin — extension ∝ force
  ✅ Gradient = spring constant (k)

• Limit of Proportionality:
  Beyond this point, extension is no longer proportional to force
  ❌ Hooke’s Law no longer applies

• Elastic Limit:
  Beyond this, the material won’t return to its original length

• Curved Region:
  Occurs after the linear region — indicates non-linear behavior

What is stress in materials science?

tress is the force applied per unit cross-sectional area of a material.

• Formula:

  Stress (σ) = Force (F) / Cross-sectional Area (A)

• Units:

  Pascals (Pa) or N/m²

What is strain in the context of material deformation?

Back:
Strain is the extension per unit length of a material when subjected to stress.

• Formula:

  Strain (ε) = Extension (ΔL) / Original Length (L₀)

• Units:

  Dimensionless (it's a ratio)

🔗 What is the Young's Modulus and how is it determined?

Young's Modulus (E) measures a material's stiffness, defined as the ratio of stress to strain in the elastic region.

• Formula:

E = Stress (σ) / Strain (ε)

• Units:

  Pascals (Pa)

• Determination:

  It's the slope of the linear portion of the stress-strain curve.

📊 What does a stress-strain curve represent?

A stress-strain curve illustrates how a material deforms under stress, showing regions of:

• Proportionality:
  Stress and strain are directly proportional (linear region).

• Elastic Behavior:
  Material returns to original shape upon unloading.

• Plastic Behavior:
  Permanent deformation occurs after surpassing the elastic limit.

• Fracture Point:
  The stress at which the material ultimately breaks.

What equipment is needed to determine the Young Modulus of a wire?

Long, thin wire of test material (e.g. copper or nichrome)

Micrometer (to measure wire diameter)

Meter ruler or measuring tape (for length)

Clamp stand & pulley (to suspend and apply force)

Slotted masses (to apply known loads)

Marker or pointer (to measure extension)

Digital balance (optional, to verify mass)

How do you carry out the Young Modulus experiment?

1. Measure the original length of the wire from clamp to marker.

2. Use a micrometer to take 3 diameter readings at different points and average them.

3. Add slotted masses incrementally to the wire via the pulley.

4. Record the extension after each added mass.

5. Calculate stress and strain for each load.

6. Plot a stress-strain graph; the gradient in the linear region is the Young Modulus (E).

How do you analyse the results in the Young Modulus experiment?

• Calculate:

  • Stress = Force / Area

  • Strain = Extension / Original length

• Plot a stress-strain graph.

• The gradient of the linear region gives the Young Modulus (E).

• Ensure accuracy by:

  • Keeping the wire vertical and taut

  • Taking repeat measurements

  • Using a thin, long wire to improve precision

• Units of Young Modulus: Pa (Pascals)

📈 How do brittle and ductile materials differ in stress-strain behavior?

• Brittle Materials:

  Fracture with minimal plastic deformation; stress-strain curve shows a short or nonexistent plastic region.

• Ductile Materials:

  Exhibit significant plastic deformation before fracture; stress-strain curve has a pronounced plastic region.

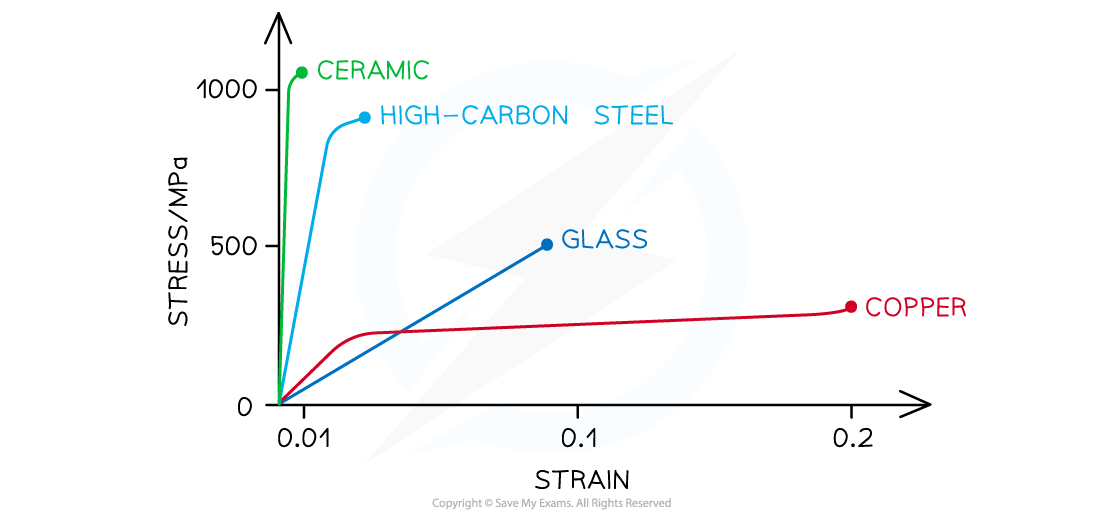
What is the ultimate tensile strength of a material?

The ultimate tensile strength (UTS) is the maximum stress a material can withstand before breaking.

• Significance:

  Indicates the material's capacity to handle stress without failure.

What is elastic strain energy?

Elastic strain energy is the energy stored in a material when it is elastically deformed (stretched or compressed) and can return to its original shape upon unloading.

What does the area under the graph represent in Force/extension graph

Work done(elastic strain energy) up until the limit of proportionality

What is the formula for calculating elastic strain energy in a material obeying Hooke's Law?

For a material obeying Hooke's Law, elastic strain energy (Eₑ) can be calculated using:

Eₑ = ½ × F × ΔL

Where:

• F = applied force (N)

• ΔL = extension (m)

Since F = k × ΔL, it can also be expressed as:

Eₑ = ½ × k × (ΔL)²

Where:

• k = spring constant (N/m)

What is the significance of the elastic limit concerning elastic strain energy?

The elastic limit is the maximum extent to which a material can be deformed and still return to its original shape. Beyond this point, the material undergoes plastic deformation, and the energy is not fully recoverable.

How does elastic strain energy relate to the conservation of energy principle?

Elastic strain energy exemplifies the conservation of energy, as the work done to deform a material is stored as potential energy, which can be fully recovered if the material returns to its original shape.

What is elastic deformation

When the load is removed, the object will return to its original shape

What is plastic deformation

• The material is permanently deformed

• When the load is removed, the object will not return to its original shape or length

• This is beyond the elastic limit and is shown in the plastic region of the graph

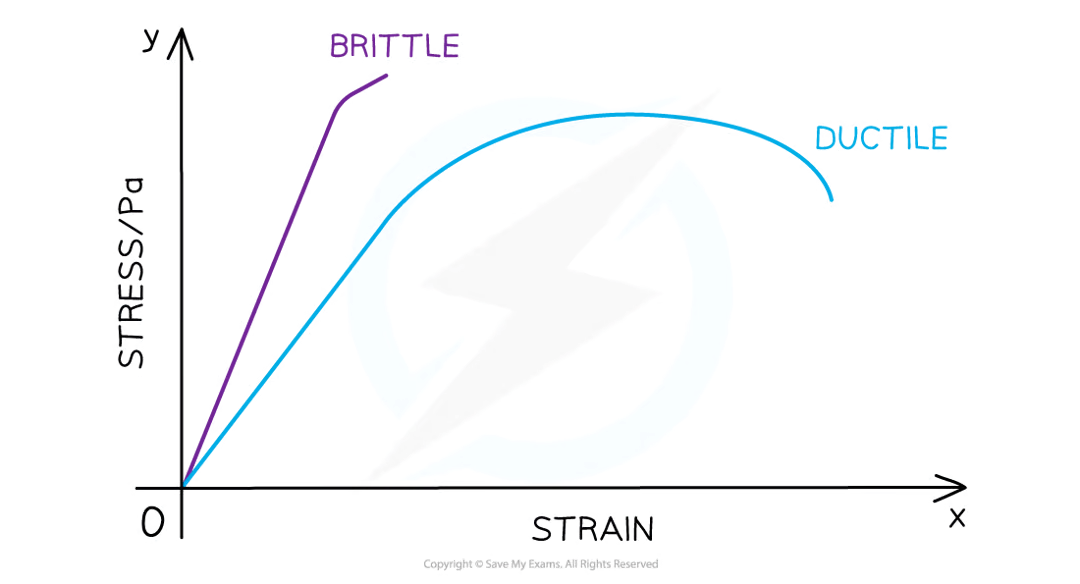
Define Brittle

materials have very little to no plastic region

Define Ductile

Materials that have a larger plastic region

What does brittle and ductile look like in a graph

What happens to a metal wire when it is loaded beyond its limit of proportionality and then unloaded? (Think in a graph format)

Loading and Unloading a Metal Wire

• When a metal wire is loaded with a force and stretched beyond its limit of proportionality, it will undergo plastic deformation

• When the force is removed, the wire is unloaded, this causes the extension to decrease

• The unloading line is parallel to the loading line (since k does not change) however, it does not go through the origin

  • If the wire is permanently deformed, it will not be at zero extension when there is no force as it is now permanently extended

• The area between the loading and unloading lines represents the work done to permanently deform the wire

What does the force-extension graph of a rubber band show about its elasticity and energy storage?

• A rubber band has no permanent extension after the load is removed — it returns to its original length.

• This means it behaves elastically.

• The graph shows more strain energy is stored during loading (stretching) than is released during unloading (contracting).

• The area between the curves represents energy lost as heat due to internal friction

Why are suspension systems important in vehicles, especially on bumpy roads?

• Suspension systems (tires, springs, shock absorbers) reduce vibrations and improve ride comfort and handling.

• Suspension helps maintain road contact and safety on uneven surfaces.

What is the function of shock absorbers in a vehicle's suspension system?

• Shock absorbers are elastic components that dampen the motion of suspension springs.

• They help keep the tires in contact with the road by absorbing energy from bumps.

• They convert the kinetic energy of moving springs into thermal energy, which is dissipated.

• The faster the suspension moves (e.g. over a bump at high speed), the greater the resistance provided by the shock absorber.