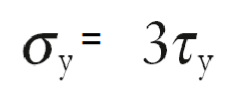Strengthening Mechanisms

MEE1004: Mechanics of Matei

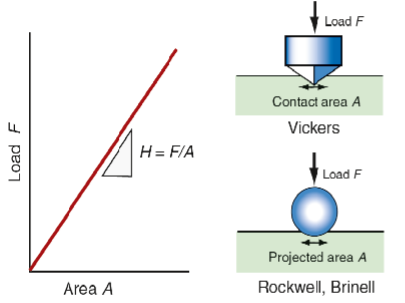
Hardness Tests

A localised non destructive measurement

Hardness test equation

F = test force

A = Surface area of indentation

σ_y = yield strength

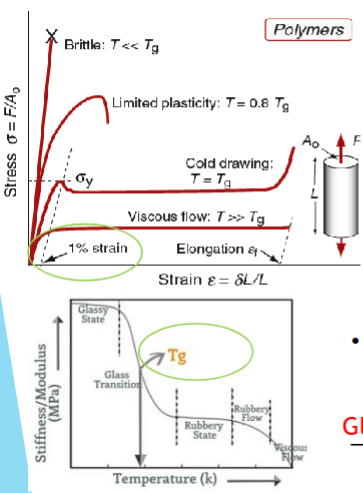
Strength of polymers

σ_y: stress at which the stress-strain curve becomes markedly non-linear. Typically around a strain value of 1%.

Behaviour beyond the yield depends on polymer’s glass transition temperature.

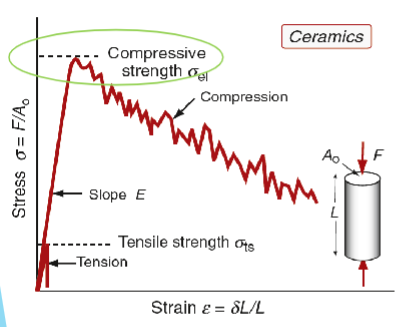
Strength of Ceramics

Yield strength never reached before material fractures.

Measurable compressive strength in used in practice elastic limit (σ_el)

Strength of a material

The force necessary to break inter-atomic bonds.

The atomic bond is broken when it is stretched to 10% of its original length.

Ideal strength equation

σ_ideal: maximum possible stress a perfect material can withstand

E: Young’s modulus of the material

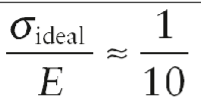
Why no material achieves ideal strength value

Defects that exist within the material, such as interior or surface cracks.

Defects in metal and ceramics

Vacancies, solute atoms, grain boundaries, dislocations

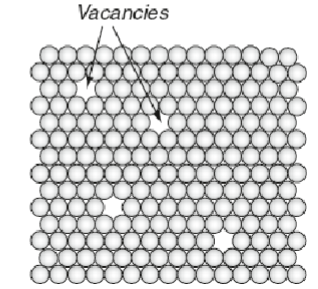
Vacanies

A site at which an atom is missing

Plays a role in diffusion, creep and sintering

They do not influence the strength of materials

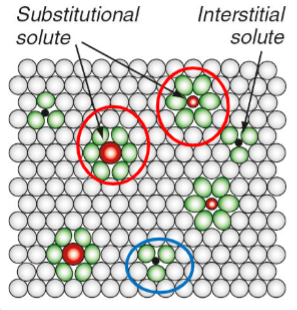
Solute atoms

Substantial solid solution: atoms replacing the host atoms.

Interstitial solid solution: Squeeze into spaces or “interstices” between the host atoms.

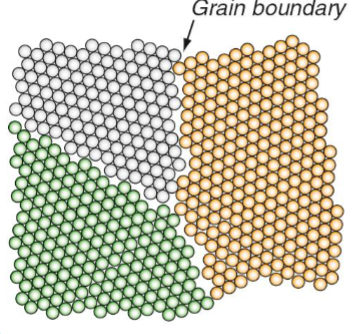
Grain boundaries

Dislocations pile up at grain boundary, creating the stress needed in the next grain to nucleate the matching dislocations.

Dislocations

An extra half-plane of atoms in the crystal which do not bond with other atoms underneath to form a continuous plane.

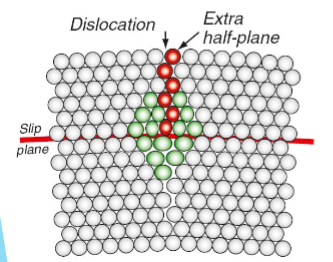
Dislocation movement

The main source of plastic deformation in crystalline materials,

Dislocation movement along shear plances

• Plastic deformation of a crystalline material corresponds to the motion of large numbers of dislocations.

• Multiple slip displacements traverse crystal = deformation at a macroscopic level.

• Dislocation prefer to move on slip planes and along slip directions.

  • Slip plane / direction with highest atomic density is preferred.

Manipulating Strength of metals

Strengthening crystallie materials by making it harder for disolations to move (i.e. enhancing the shear yield strength).

Dislocation pinning

A mechanism that halts a dislocation’s movement, requiring a greater amount of force to be applied to overcome the barrier.

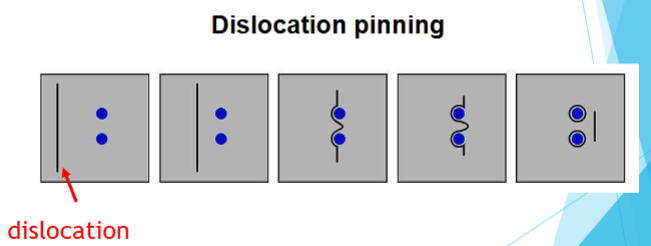
How metals are strengthened

1. Solution hardening (alloying),

2. Dispersion and precipitate strengthening,

3. Work hardenung / strain hardening,

4. Grain boundary hardening

Solution hardening (alloying)

Strengthening of metals by alloying - deliberate additions of impurities (solutes).

Alloying process strengthens the metal by adding other elements that disperse atomically into the host lattice.

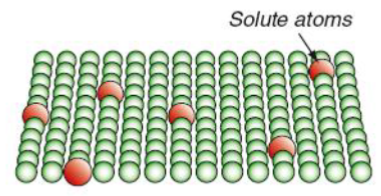
Ways to increase the effectiveness of alloying

Increase amount of alloying element, increases solid solution strengthening.

Increase the size difference between the alloying elemets and the host material, the harder it is for dislocations to move.

Increase amount of alloying elements increase soid solution strengthening.

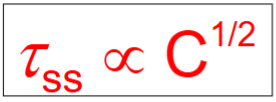
Calculating the contribution of solid solution to the shear stress required to move the dislocation

C = concentration of solute

τ_ss = additional shear stress required due to solid solution strengthening

Dispersion

Disperse small, strong particles of higher melting point into a liquid metal, the particles trapped when metal cast into shape (e.g. metal matrix composite, Al-SiC).

Precipitation

A heat treatment process that produces uniformly dispersed particles within a metal’s grain structure.

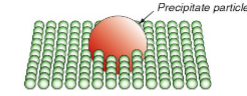
Precipitation hardening

Makes it more difficult for the dislocation to shear and travel across them.

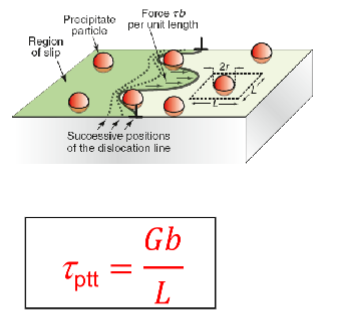
Shear stress required to move dislocation due to disperion and precipitate strengthening

τ_ppt = shear stress required to move dislocation

L = spacing of particles

G = alloy shear modulus

b = magnitude of slip factor

Work hardenigng

Caused by accumulation of dislocation generated by plastic deformation.

Work hardening and shear stress

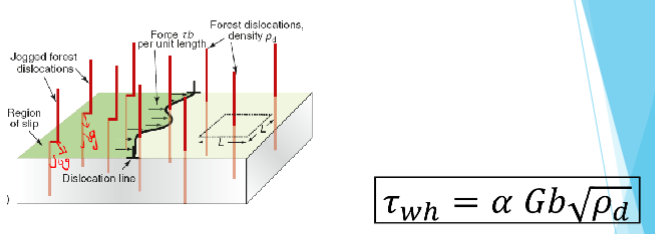
Contribution of work hardening to the shear stress required to move the dislocation

Work hardening and shear stress equation

τ_wh: shear stress required to move the dislocation

α: constant

G: shear modulus

b: length of jogs

ρ_d: density of dislocation

Dislocation density

The length of dislocation line per unit volume (m/m³).

Dislocation density equation

Dislocation density: total dislocation length/unit volume

Another word for work hardening

Strain hardening

Examples processes for strengthen metals through cold working (work hardening)

Rolling, forging, extrusion and drawing.

Grain boundary hardening

Method of strengthening materials by changing their average crystallite (grain) size.

Effects of grain boundaries on the shear strength required for a dislocation to move

τ_gb: shear stress

D : grain size (typically 10 - 100 μm)

Can strengthening mechanisms be used in combination

Yes

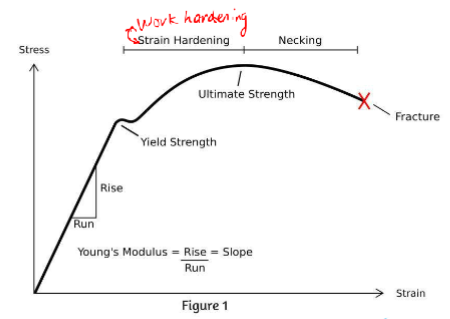
Strength and ductilility

An increase in strength will lower the ductility

(lower elongation to fracture, i.e. more brittle)

Approximation of shear yield strength based on strengthening mechanisms.

How to link tensile yield strength to the shear yield strength

Θ is the angle between shear plane normal and the tensile loading direction

Dislocations will move on the slip plane on which this shear stress is the greatest

Maximum shear stress lies at an angle of 45 when τ = σ/2, i.e. σ_y ∝ τ_max

Strengthening polymers and relative slippage

For strengthening polymers, relative slippage of polymer chain must be considered.

Impeding the slippage of molecular chains can be done through blending, drawing, cross-linking, and by reinforcement with particles, fibres and fabrics.

Crystal resistance to dislocation

Crystals resist the motion of dislocations with a friction-like resistance (lattice resistance) f per unit length.

Dislocation move if τ > f/b

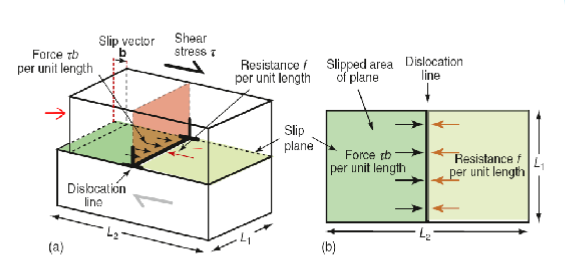
Calculating tensile stress required to cause yielding

Tensile stress required to cause yielding is 3x the shear strength of a single crystal.