Intro to AI: Machine Learning, Types of Learning, K Calculations

Machine Learning

• Subset of AI that deals with learning agents

• Doesn’t require us to directly manipulate it

• Based on past experiences or data to arrive at an output

Deep learning

• Part of ML involving artificial neural networks

• Deep because if more than 3 layers then deep learning

How can you say an agent is learning?

Is learning if it improved performance after making observations about the world

Machine Learning when an agent is a computer

• Observes data

• Build a model based data

  • Model: hypothesis about the world and software that can solve problems

Types of Learning

1. Supervised learning

   • Learn a function from labeled data

   • EX. There’s an answer key

2. Unsupervised Learning

   • Learn patterns from unlabeled data

   • Output is not labeled but you can still make sense of it

3. Reinforcement Learning

   • Learn best actions from experience of rewards and punishments

   • Learning by itself

Supervised Learning

• Labeled data

  • Input-output pairs where label is the output

• Agent is taught by examples of labeled data

What does Supervised Learning do with labeled data?

• Observes the labeled data and learns a function or builds a model based on that data

• Uses the function or model to process input data and give an output

Types of Supervised Learning

1. Classification

2. Regression

Classification

• Output:

  • Finite set of values called classes or labels

  • EX. true/false, sunny/rainy/cloudy

• Agent learns from observed values to determine what label new observations belong

Regression

• Output: 

  • Number

  • EX. temperature, which can be an integer or a real number

• Agent estimates and understands the relationship among variables

• Useful for prediction and forecasting

Supervised Learning Algorithms

1. Nearest neighbors

2. Decision trees

3. Neural networks

4. Support vector machines

5. Linear regression

Unsupervised Learning

• Agents learn patterns from input without feedback (unlabeled data)

• Example:

  • Input: Images of animals

  • Output: Groups of similar images

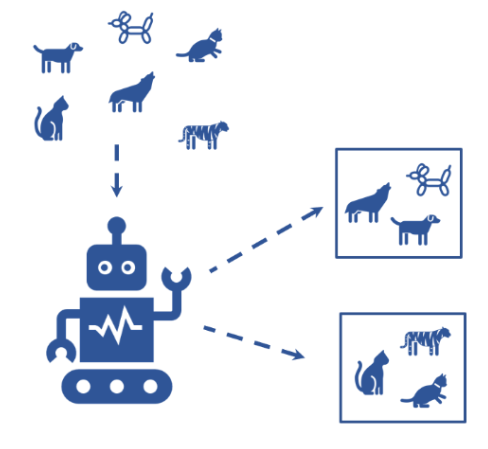
Types of Unsupervised Learning

1. Clustering

2. Association Rule Mining

Clustering

• Input

  • Unlabeled dataset

• Output

  • Sets of similar data (based on defined criteria)

• Useful for discovering segments in data and applying different business strategies for each segment

Association Rule Mining

• Output

  • Correlations and associations

• EX. Which items shoppers tend to purchase together (frequently bought together or market basket analysis)

Unsupervised Learning Algorithms

1. K Means Clustering

2. Hierarchical Clustering

3. Gaussian Mixture Models

4. Apriori Algorithm (Association rule mining)

Reinforcement Learning

• Agent learns from rewards and punishments

  • Decides on actions towards more rewards

• Agent needs to balance exploration and exploitation

Exploration VS Exploitation

• Exploitation: stay with what has given most reward

• Exploration: try other options to get additional information

• EX:

  • Gambling agent that:

    • Chooses a slot machine that gave the most returns (reward)

    • Avoids slot machines that have not (punishment)

Reinforcement Learning Algorithms

1. Q-Learning

2. State-Action-Reward-State-Action (SARSA)

3. Deep Q Network

Input of Classification

Labeled Dataset

• Instances with labels

  • Instances = examples

Classification: What would an instance need to have?

• A set of features/attributes

• A label

Instances = ______

Features = ______

Labels = ______

Rows, Columns, Last Column (usually)

What is the goal of Classification?

• Derive a function (also called a model) based on a dataset

• Predict the label of an instance with unknown label

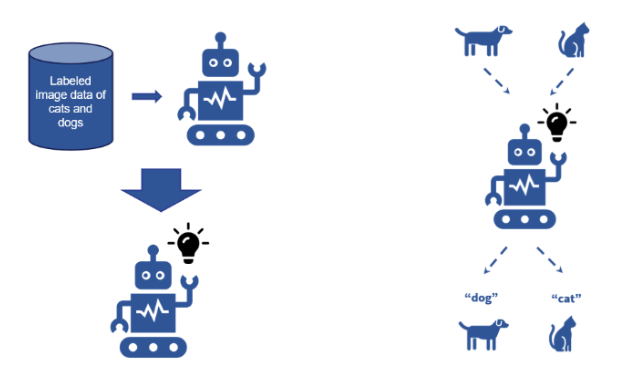
Steps to Training and Testing a Machine Learning Model (Supervised Learning)

1. Model Training

2. Model Testing

Steps to Training and Testing a Machine Learning Model (Supervised Learning): Model Training

• Start with labeled dataset

  • Features X is the input

  • Labels Y is the target used by the model to make predictions

• Model learns from labeled data

• Goal: learn the relationship between features and labels, so it can later make accurate predictions

Steps to Training and Testing a Machine Learning Model (Supervised Learning): Model Testing

• Use test features (data that model never saw) to evaluate model

• Model uses test features to make predicted labels (output classfications made by model)

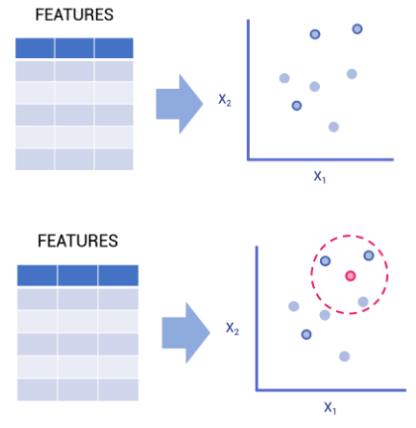
Classification Models: Nearest Neighbors or K Nearest Neighbors

• Instances as labeled datapoints in a graph

  • Features = “coordinates”

• For an unlabeled instance

  • Get the K nearest points

  • Get the label that represents most of these points

Classification Models: Decision Trees

• A sequence of tests (decisions) induced from dataset

  • Each test is based on 1 feature

  • Eventually leads to a predicted label

• Goal: A tree that consistently leads to the correct labels

• Use first the feature that can best distinguish examples by their labels

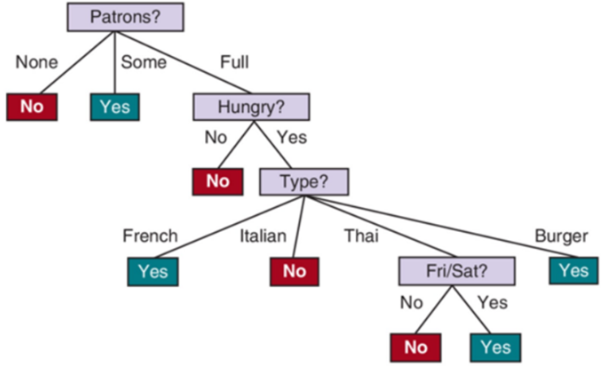
What’s the problem with a decision tree?

Overfitting

• Fits well with training dataset, but does not do well with new instances

• Solution: Random Forest

Classification Models: Random Forest

• Predict labels based on multiple decision trees

• Each decision tree is from a random sample of the main dataset

• “ensemble method”

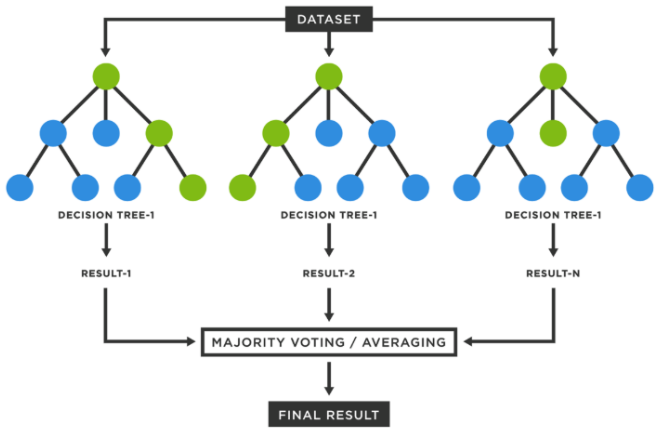
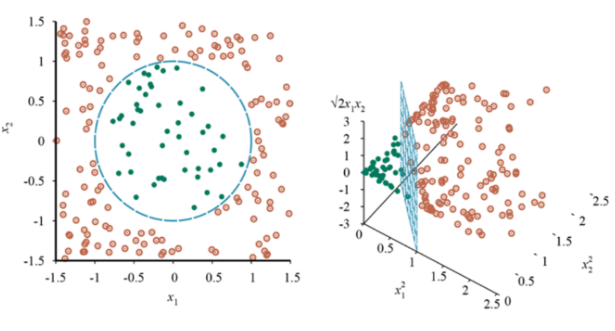
Classification Models: Support Vector Machines (SVM)

• Instances as datapoints, and features as dimensions in a hyperplane

• Goal: Linearly divide the labeled datapoints in the dataset

  • Make new dimensions if cannot separate

  • “Support Vectors”: points closest to boundary

• Good in practice; popular in the early 2000s

Classification Models: Artificial Neural Networks (ANN)

• ANN: layers of neurons connected to each other

  • Input layer: takes in input signals (like features)

  • Output layer: provides the output (like labels) 

  • Hidden layers to facilitate computations

  • Each layer influence the neuron activation of succeeding layers
    

• Most common method in the past few years!

  • Deep learning = multiple hidden layers

• Uses back propagation to learn weights and thresholds

In an ANN, a “neuron” is activated based on what?

• Input signals

• Weights

• Thresholds

• Activation function

Among the classfication models, which one is the most recently popular?

Artificial Neural Networks (ANN)

Because of deep learning (multiple layers)

How do we evaluate a classification model

Split the dataset:

• Training set: used to train the model

• Test set: used to evaluate the model

Model Evaluation of a Classification Model: Computing for Accuracy

Accuracy = # of correct predictions / # of total predictions

Model Evaluation of a Classification Model: Confusion Matrix

Show correct results against predicted results for each class (i.e. possible values of label)

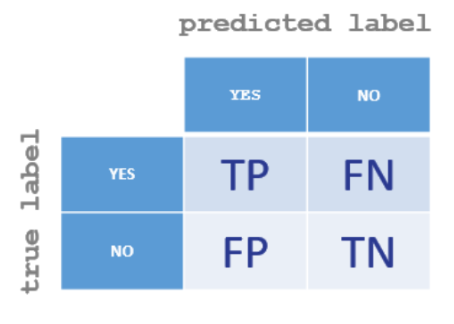
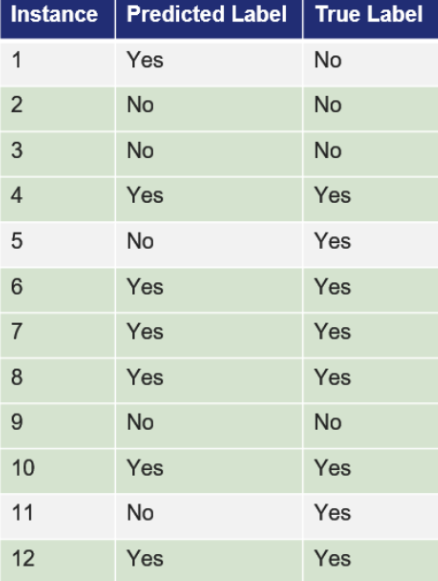
Do the Model Evaluation for this example

Accuracy:

Number of test instances: 12

Number of correct predictions: 9

9/12 = 0.75 or 75%

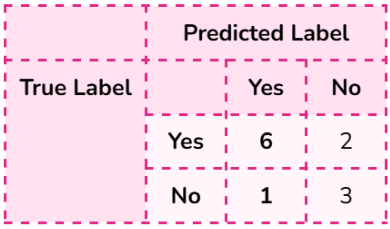
K Nearest Neighbors (KNN) Goal

• Goal: Given a new unlabeled instance, predict its label based on nearest neighbors

KNN For an unlabeled instance

1. Get the k nearest points

   • What is the basis of what’s considered “nearest”?

   • What do we do with non-numeric values?

2. Get the label that represents most of these points

   • What do we do with ties?

3. Conclude that the instance belongs to the representative label

Distance Metrics to Choose from for KNN

• Euclidean distance

• Manhattan distance

• Hamming Distance

  • For binary/categorical data

Data Transformation Options for KNN

• Non-numeric values

• Scale issues

Ways to Determine Majority Vote KNN

Dealing with Ties and Appropriate k

Euclidean Distance

• Assumption: different dimensions are comparable

• For 2D plane: √(x₂-x₁)²+(y₂-y₁)²  (where x and y are points)

• For multiple features: √(△ x₁)²+(△ x₂)²  + … + (△ x_m)² (where x is a column)

Manhattan Distance

• Best for datasets where additive differences of features are more appropriate

• Add absolute values of column differences

• Formula: | Δ x₁ | + | Δ x₂ | + … + | Δ x_m |

Other Metrics for Distance

Minkowski Distance

Cosine Distance

Minkowski Distance

• Generalization based on value p

• Includes Manhattan distance (p = 1) and Euclidean distance (p = 2)

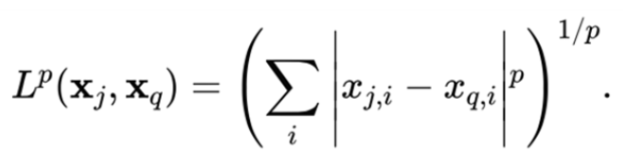
Cosine Distance

• 1 – cosine similarity

• Inspects the angle between vectors

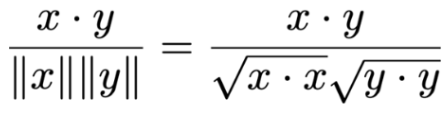
What’s the problem that can arise with these metrics?

Scaling

Categorical Features

Problem: Scaling

• Some metrics work when values are of the same scale

• Represent same info, but the scale of values are different 

• Features with much larger values tend to overshadow features with smaller values

• Solution: normalize data

Problem: Categorical Features

• Measuring distance between non-numerical features

  • Patrons: Some, None, Full

  • Type: French, Italian, Thai, Burger

• Possible Solutions:

  • Convert to numbers

  • Count attribute matches

Hamming Distance

• Used for categorical features

• Counts number of mismatches among features

• Closest point is when all features match

• Works for KNN since you still get smallest values

How do we know which Distance metric to use?

• Depends on dataset (usually default euclidean)

• Important to consider scale and categorical data

• Crucial to transform data before choosing and applying a metric

• Try to reduce the variance

Why transform data?

• “Format” of data incompatible with distance metric

• Can’t apply same distance metric if inconsistent format among features

• Inconsistent scaling can skew results to favor certain features

Data Transformation Types

1. Categorical to numerical

2. Numerical to categorical

   • Convert to levels

   • Bins

3. Consistent scaling: normalization

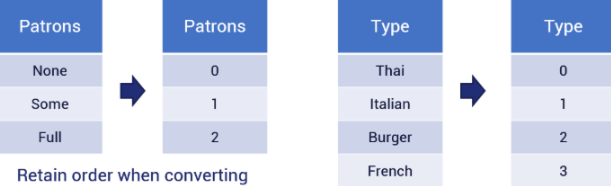
Data Transformation: Categorical to Numerical

Assign a number to each value type

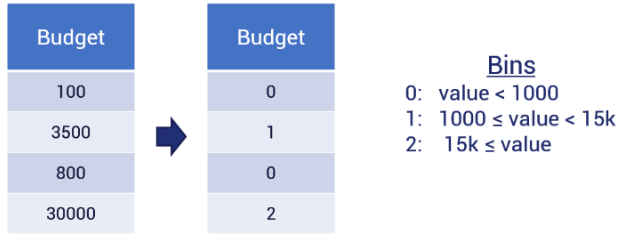
Data Transformation: Numerical to categorical

• Usually do this if using Hamming distance

• No need to convert numbers if there are only a few values

• If there are many possible values (or even infinite), we can divide values and assign them to bins

Data Transformation: Consistent scaling: normalization

• Definition: scale down dataset so that all values fall between 0 and 1

• Reduces bias on data

• Standard preprocessing step in machine learning

• Improves generalization, enabling better predictions on new data

Types of Scaling under Normalization

• Min-Max Scaling

• Standard Scaling

Min-Max Scaling Formula

x: value to be scaled

min: minimum value of the feature

max:maximum value of the feature

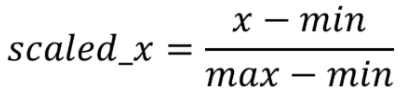
KNN: Majority Vote

After getting nearest points, label of majority is predicted label of new instance

EX. 2 Blue, 1 Red

Majority Label: Blue

Why do we usually choose an odd value for k in KNN?

To reduce the chances of a tie when determining the majority vote among nearest neighbors

True or False: Ties still occur in KNN even if k is odd?

True — Ties can still happen if two or more points are equally distant from the new instance, increasing the number of nearest points considered.

Give an example of when a tie might still occur in KNN even with an odd k.

If k = 3 and two points share the same distance for the 3rd nearest neighbor (e.g., both 1.50 units away), you’d effectively have 4 nearest points — causing a tie.

What can we do if ties cannot be completely avoided in KNN?

Apply tie-breaking methods

• Random label choice

• Consulting a domain expert

• Comparing the next nearest instance

• Weighting closer instances more heavily

How do we know which k to use?

• Train multiple kNN models with different values of k

• Apply evaluation methods (e.g. accuracy) on each model and pick the one that performs best

What factors affect how long KNN takes to predict a label for one instance?

• Each prediction requires multiple distance computations

  • The number of instances in the training set

• Each distance computation requires multiple operations

  • Proportional to the number of features

In KNN, what do the “operations” in distance computation depend on?

The number of features — each feature requires operations like squaring, adding, etc.

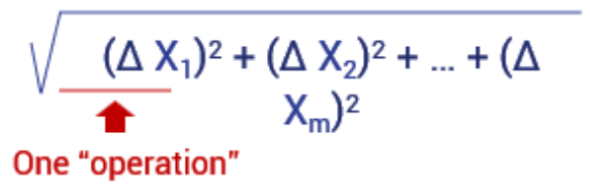
kNN’s time complexity for one new instance

O(mn)

• m: number of features

• n:  number of instances (training set)

Questions to Ask/Answer when making a decision tree

1. How do we branch and determine terminal node?

2. How do we choose which features to use for branching?

GINI Index: How do we choose which feature to use?

1. For each feature, compute Gini index for each of its categories

2. Compute for the weighted average of the feature’s Gini indices

3. Select the feature with smallest (weighted average) Gini index

GINI Index Steps

1. Identify target label (outcome you’re trying to predict)

2. List all features (attributes)

3. Compute GINI for each category of a feature

4. Compute Weighted Average GINI for the feature

5. Repeat for other features

6. Choose feature with lowest Weighted Gini

7. Repeat process for each branch

What to do with new groups?

• Leaf (terminal node)

  • All instances in the group have the same label

  • E.g. all yes or all no

• Branch

  • Instances have mixed labels 

  • e.g. mix of yes and no

  • Considered as a new group to split

GINI Index Formula

GINI = 1- (j₁ / total of t)² - (j₂ / total of t)²

t : node (e.g. the category like none/some/full for Patrons)

j : class (e.g. the label like Yes/No for Will Wait)

p ( j | t ) : relative frequency of the class in the group

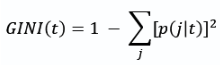
How do we compute for the weighted average of the feature’s Gini indices?

• multiply GINI(category) by:

total # in category / total # in all categories

• Then sum all values to get the weighted average

• Aka GINI split

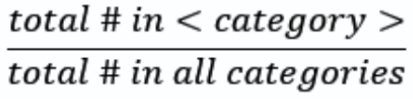
In a decision tree, number of branches equals to what?

number of categories

Clustering

• Type of unsupervised learning (unlabeled data)

• Learn patterns and derive groups (clusters) of similar instances

• Each unlabeled instance is assigned to a cluster

Examples of clustering methods

• K-Means clustering

• Hierarchical clustering

• Gaussian mixture models

• Spectral clustering

How do we evaluate clustering results?

• Inertia (elbow method)

• Silhouette score

K-Means Clustering

• Intuition: instances in the same cluster should be close to each other

1. Specify k: target number of clusters

2. Select k random instances as centroids of their clusters

3. Repeat

   • Assign each instance to the cluster of the closest centroid

   • For each cluster, get the mean for each feature and set the new centroid

4. Stop when cluster memberships stop changing

Hierarchical Clustering

• Dendrogram

• Instances =  terminal nodes

• Branches connect nodes/subgroups at different levels

• Clusters can be derived from a dendrogram

Dendrogram

• Tree diagram depicting closeness through its branches

• Branches show which instances/groups are close to each other

• Derive clusters from generating a dendrogram

2 ways to generate a dendrogram

• Agglomerative clustering: bottom up

  1. Start with treating each instance as one cluster

  2. Repeatedly merge 2 closest clusters 

• Divisive clustering: top down

What can other Clustering Methods handle that K-Means cannot?

non-spherical boundaries

Other Clustering Methods

1. Gaussian Mixture Models

2. Spectral Clustering

Gaussian Mixture Models

• Soft assignment since there’s a probability (?)

• Learns a pattern from the dataset so it can make different gaussian models from the different probabilities

• Covariance, not just means, determine the shape

Spectral Clustering

• More based on whether it’s connected

• Affinity (closest pair wise) and degree of connection to the next value 

• Graph-based machine learning technique that uses the eigenvectors of a graph's Laplacian matrix to find clusters within data, especially for non-convex shapes

Clustering Evaluation: How do we know if a clustering result is good?

Base it on

• Homogeneity

• Heterogeneity

Homogeneity

• How similar the instances are within a cluster

• More homogenous = more similar

• Points in a cluster should ideally be similar to each other

Heterogeneity

• How different the instances are across different clusters

• More heterogeneous = more different

• The further points are from one cluster to another, the better

How do we ensure best quality of clustering?

Try clustering methods with different k values and get the clustering with the best quality

Inertia

• Measures homogeneity (within cluster sum of squares)

• Elbow method to estimate best k

• within-cluster sum of squares of distances

• You want to keep inertia low

Silhouette score

• Measures and weighs both homogeneity and heterogeneity

• Compute a score for every instance, and then get the average

  • Homogeneity score

  • Heterogeneity score

  • Combining the homogeneity and heterogeneity scores

Steps to Compute Inertia

1. For each cluster, determine the cluster centroid

2. For each instance, square its distance from its cluster centroid

3. Sum all these squares

Inertia Formula

C: cluster

i: instance

d(i, μ(C)): distance between i and cluster C’s centroid

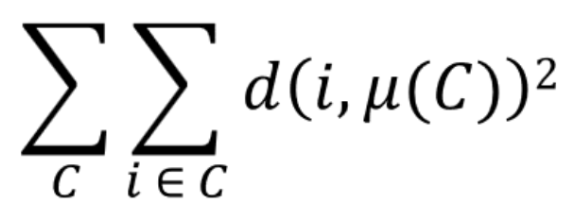
Inertia: Elbow Method

• Used when picking between multiple k-means clusterings (different values of k)

• Provides a balance between low k and low inertia

• Process involves calculating a metric called inertia (AKA Within-Cluster Sum of Squares, or WCSS) and plotting it. 

Inflection point

• Tangent line forms an angle closest to 45 degrees

• Determines the best k

• In practice, we often just estimate from the shape of the graph

Inertia: Elbow Method Steps

1. Perform K-Means with different k values

2. Get the inertia score for each final clustering

3. Plot the k values and inertias

   • x-axis: k values

   • y-axis: inertia

Silhouette Score: a(i): homogeneity score

• Get the average distance between the instance and other instances within the same cluster

• The smaller, the better

Silhouette Score: b(i) heterogeneity score

• Get the average distance between an instance and instances from its nearest neighboring cluster

• The larger, the better