PHIL 210

Logic

the study of what follows from what in virtue of their logical form

Valid

no case where all its premises are true and the conclusion is false

Invalid

there is at least one premise where all the values are true and the conclusion is false

Metalanguage

a language used to describe another language

Affirming the consequent

a fallacy of switching the cause and the consequence

it is not the case that

• is not

• does not

‘both A and B’

• and

• but

• even though

• although

‘either A or B or both

• or

• unless

If ‘A’ then ‘B’

• Is A then B

• If A, B

• A only if B

• provided A, B

• B provided A

• B if A

A if and only if B

• if and only if

• just in case

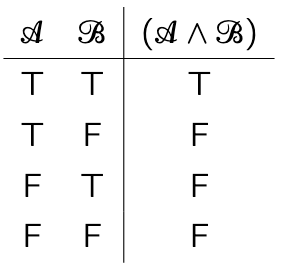
Conjunction TT

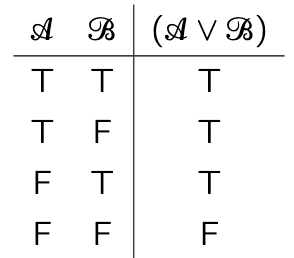
Disjunction TT

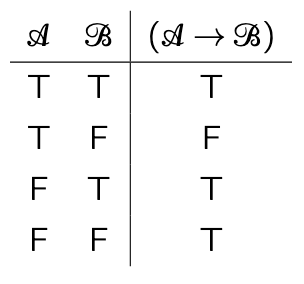
Conditional TT

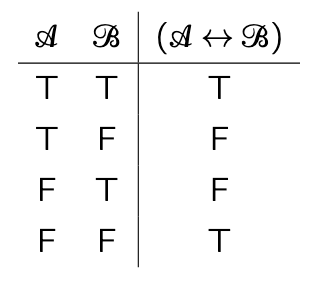
Biconditional TT

Negation TT

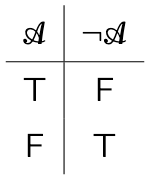
Base clause

Every sentence letter is a sentence, called an atomic sentence

Second clause

Is A is a sentence , then -A is a sentence

Third clause

If A and B are sentences, then, (A /\ B) is a sentence

Fourth clause

If A and B are sentences, then, (A \/ B) is a sentence

Fifth clause

If A and B are sentences, then, (A → B) is a sentence

Sixth clause

If A and B are sentences, then, (A ←> B) is a sentence

Seventh clause

Nothing else is a sentence

when is TFL valid

no valuation in which all premises are T and the conclusion is F

TFL is invalid

if there is at least one valuation that makes all premises T and the conclusion F

Equivalence

two sentences A and B are equivalent in TFL iff every valuation either makes both A and B true or makes both A and B false

(A → B)

( - B → - A)

( A /\ B)

-(-A \/ -B)

-(A /\ B)

(-A \/ -B)

-(A \/ B)

(-A /\ -B)

(A \/ B)

-(-A /\ -B)

A ←> B

((A → B) /\ (B → A))

— — A

A

Tautology

when the TFL is true on every valuation

necessary truth

tautology

Contradiction

when the TFL is false on every valuation

necessary falsehood

contradiction

Tautology and entailment

when there is a tautology then the statements always entail the other

converting tautology to a sentence

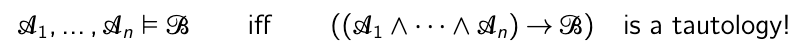
Contingent

A sentence that is neither tautology or a contradiction

Joint satisfiability

when there is at least one valuation which makes multiple sentences true

Jointly Unsatisfiable

When they are not jointly satisfiable

Proof

a finite sequence of sentences, such that each element in this sequence is either a premise or obtained from earlier sentences by the application of an inference rule

Proof system

a formal framework for proofs, consisting of a formal language and a fixed set of inference rules

Distinction between l- and l=

the l- is a syntactic rule

the l= is a semantic rule

sound proof-system

when the semantic notion of deduction corresponds to the semantic notion of entailment

Introduction ‘I’

introduces a new kind of connective into a sentence

Elimination ‘E’

eliminates a connective from a sentence

relationship between tautologies and premises

a biconditional relationship where whatever sentence you can prove from no premise will be a tautology

soundness

if an argument is sound then we may assume that if it is provable then it is also entailed

completeness

if an argument is complete then we may assume that if it is entailed then it is also provable