Graphs

Grpahs, graph traversals and graph implementations

What are neighbours?

Two nodes are connected by an edge

What is the degree of a node?

The number of other nodes that it is connected to (i.e. the number of neighbours that it has)

What is a loop?

An edge that connects a node to itself

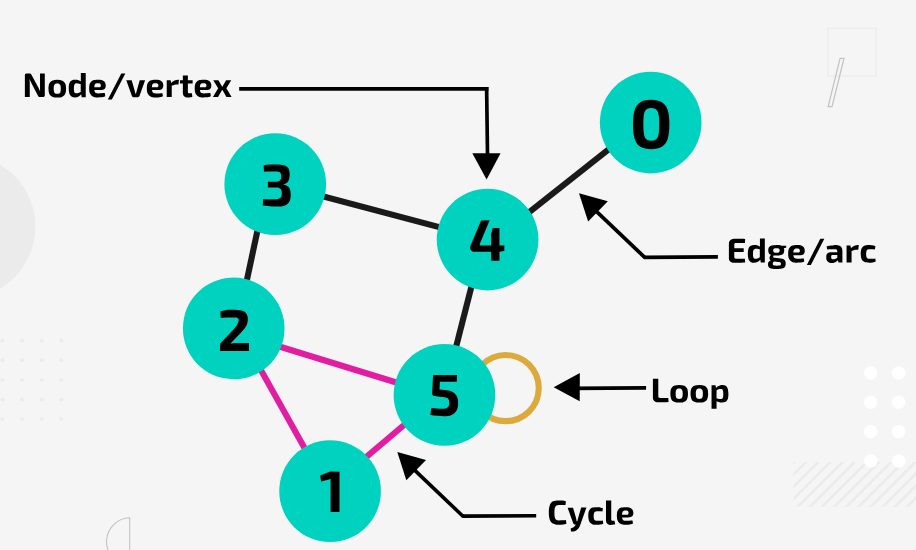
What is a path?

A sequence of nodes that are connected by edges

What is the length of a path (path length)?

The number of edges in a path

What is a cycle?

A path that starts and ends at the same node (and no node is visited more than once)

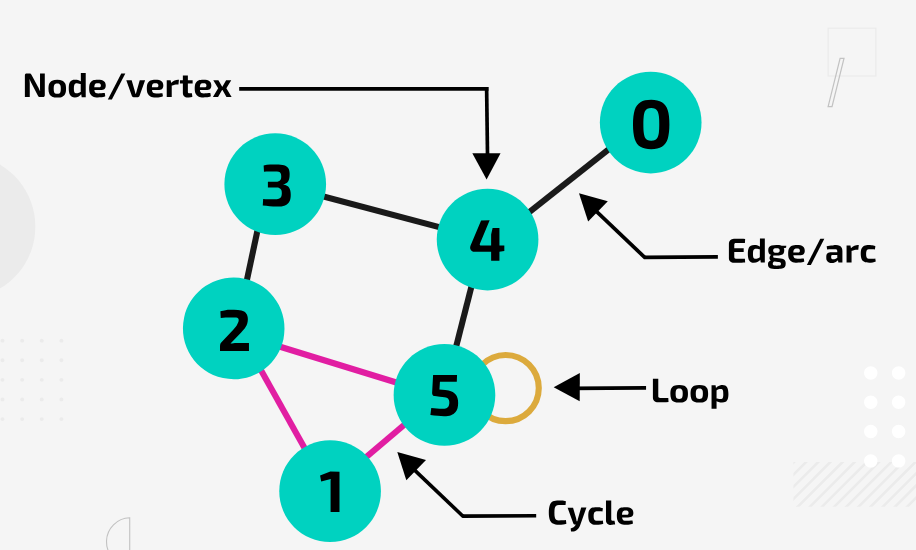
What is an undirected graph?

A graph allows you to move (traverse) in either direction between nodes.

How are the edges of an undirected graph shown in diagrams?

The edges are simple lines, not arrows.

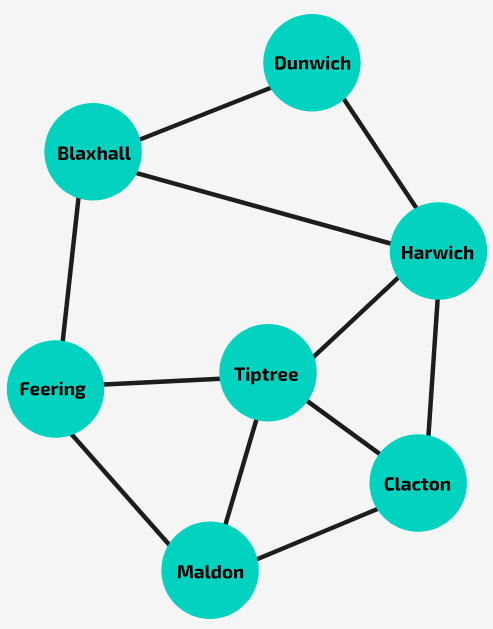
In the graph shown in the image, is Feering → Maldon → Tiptree → Harwich → Clacton → Tiptree → Feering a cycle?

No! In a cycle, no interim node can be visited more than once. In the example given, Tiptree is visited twice.

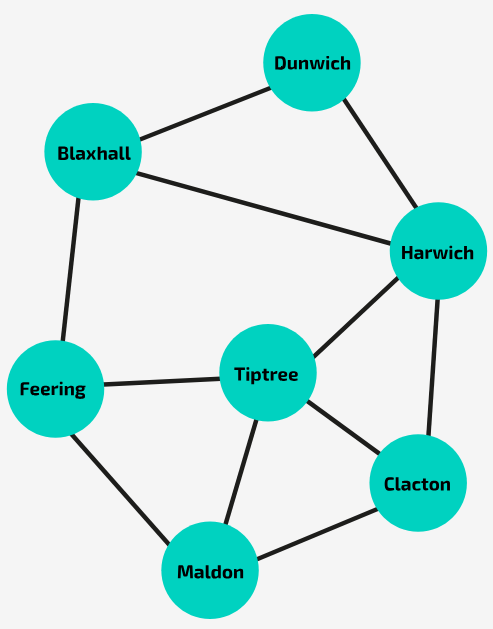
How many neighbours does Tiptree have?

4

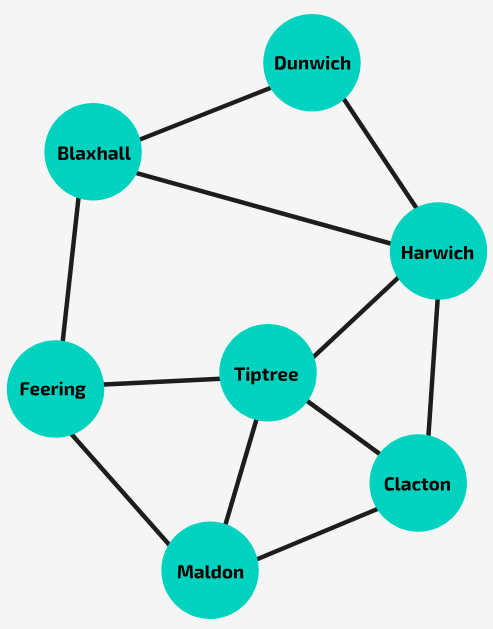
What is the degree of Tiptree?

This is the same as sking how many neighbours it has - 4

What is a directed graph (aka digraph)?

A graph in which the edges have direction, which means that you move between nodes in a specified direction.

How are the edges of a digraph represented in diagrams?

• Arrows are used (instead of lines) to represent the edges.

• If the edge is bidirectional, two arrows are used (or sometimes double-headed arrows).

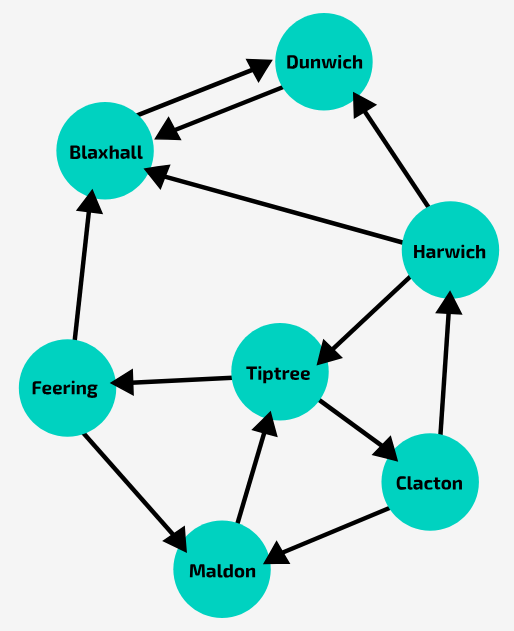
In the graph shown in the image, is Harwich → Clacton → Tiptree → Harwich a cycle?

No, because there is no edge from Harwich directed towards Clacton, nor from Clacton towards Tiptree, nor from Tiptree towards Harwich.

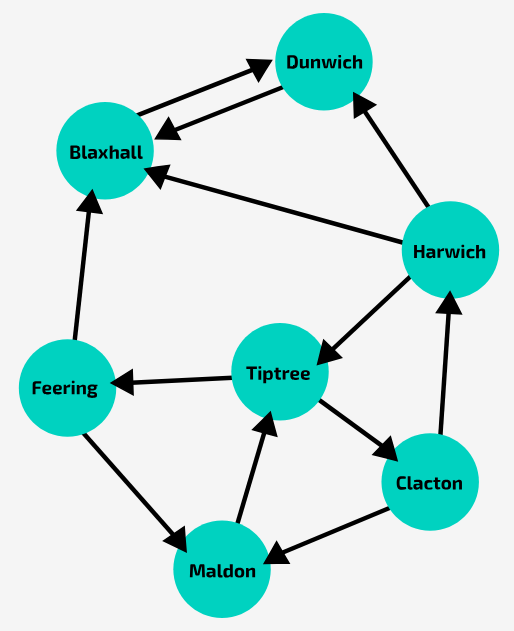
In the graph shown in the image, is Harwich → Tiptree → Clacton → Harwich a cycle?

Yes

Describe how a tree is related to a graph

A tree is a connected, undirected graph with no cycles.

• Connected means there is always a path between any two nodes in a tree. This means there is no node, or set of nodes, that is disconnected from the others.

• Unidrected so none of the edges in a tree are directed.

• There are no cycles in a tree, which means that there is only one possible path between any two nodes.

Is a tree traversal more or less complex than a graph treversal, and why?

A tree traversal is less complex than a graph traversal because a tree has no cycles.

What is a weighted graph (aka labelled graph)?

A graph that has values associated with each edge. Weighted graphs can be either directed or undirected.

Why are weighted graphs useful?

• The weights can be used to record information relating to the edges.

• For example, in a mapping application, you may want to record distance between towns, or the time needed to travel between one town and another. Weights will enable you to find the shortest path between nodes.

What is a graph traversal?

The process of systematically visiting each node in a graph

What must we keep track of during a graph traversal?

We must keep track of the state of each node. There are three states for each node:

• Unvisited – the node has not yet been encountered

• Discovered – the node has been encountered (partially explored) but will need to be returned to

• Visited – the node has been fully explored and does not need to be returned to again

As the traversal progresses, the state of each node will change.

Why must we keep track of the state of each node?

A graph can have cycles, and unless you keep a track of where you have been and where you have yet to go, you can end up going round in circles.

What is a common use of a breadth first search of a graph?

To find the path containing the least number of nodes between two points in an unweighted graph.

Describe the breadth first search algorithm for a graph in structured English

Declare the discovered list
Initialise a queue
Set found to False

Add start node to the discovered list
Enqueue the start node

While the queue is not empty and the target has not been found
Dequeue an item to become the current node
For each neighbour of current node
If neighbour is not in the discovered list
If neighbour is the target node
Set found to True
Else
Add the neighbour to the discovered list
Enqueue the neighbour
Return found

Write a breadth first search function in psuedocode that:

• Starts at a given node called start_node

• Searches for a given node called target_node

• Returns if the target_node was found

The graph is represented as a dictionary, like the one shown in the image

FUNCTION breadth_first_search(graph, start_node, target_node)

    IF start_node == target_node THEN
        RETURN true
	
    // Initialisation
    LIST queue = [start_node]
    LIST discovered = [start_node]
    LIST neighbours = []
    found = False

    // Repeat while there are items in the queue
    // and the target node has not been found 
    WHILE LEN(queue) != 0 and found == False
        
        // Set the current node to the first item in the queue
        current_node = queue[0]

        // Remove the current node from the start of the queue
        queue.REMOVE(0)

        // Get the current node's list of neighbours
        neighbours = graph[current_node]

        // Repeat for each node in the neighbours list
        FOREACH node IN neighbours
            // Check if the node has not already been discovered
            IF discovered.CONTAINS(node) == False THEN
                // Check if the target node has been found
                IF node == target_node THEN
                    found = True
                ELSE
                    // Add the node to the stack 
                    // and to the discovered list
                    queue.APPEND(node)
                    discovered.APPEND(node)
                ENDIF
            ENDIF
        NEXT node
    ENDWHILE
                    
    RETURN found
ENDFUNCTION

What is a common use of a depth first search of a graph?

To determine whether there is a path between two nodes of a graph. Remember that a graph (unlike a tree) does not need to be fully connected.

Describe the depth first search algorithm for a graph in structured English

Declare the discovered list

Initialise a stack

Set found to False

Add start node to the discovered list

Push start node onto the stack

While the stack is not empty and the target has not been found

Pop the item from the top of the stack to become the current node

For each neighbour of current node

If neighbour is not in the discovered list

If neighbour is the target node

Set found to True

Else

Add the neighbour to the discovered list

Push the neighbour onto the stack

Return found

Write a depth first search function in psuedocode that:

• Starts at a given node called start_node

• Searches for a given node called target_node

• Returns if the target_node was found

The graph is represented as a dictionary, like the one shown in the image

FUNCTION depth_first_search(graph, start_node, target_node)

    // Initialisation
    LIST stack = [start_node]
    LIST discovered = [start_node]
    LIST neighbours = []
    found = False

    // Repeat while there are items in the stack
    // and the target node has not been found 
    WHILE LEN(stack) != 0 and found == False
        
        // Pop the top item from the stack to be the current node
        current_node = stack.POP()

        // Get the current node's list of neighbours
        neighbours = graph[current_node]

        // Repeat for each node in the neighbours list
        FOREACH node IN neighbours
            // Check if the node has not already been discovered
            IF discovered.CONTAINS(node) == False THEN
                // Check if the target node has been found
                IF node == target_node THEN
                    found = True
                ELSE
                    // Push the node onto the stack 
                    // and add it to the discovered list
                    stack.APPEND(node)
                    discovered.APPEND(node)
                ENDIF
            ENDIF
        NEXT node
    ENDWHILE
                    
    RETURN found
ENDFUNCTION

What are the two established ways of implementing a graph?

• The adjacency matrix

• The adjacency list.

What is an adjacency matrix?

A two-dimensional array that records the relationship between each node and all other nodes in the graph.

How are edges represented in the adjacency matrices of unweighted graphs?

For unweighted graphs:

• 1 is set when an edge exists between two nodes

• 0 is set when there is no edge between two nodes

Is the data in an adjacency matrix for an undirected graph symmetric?

• Yes (imagine diagonal line from the top left-hand corner to the bottom right-hand corner in the example shown)

• This is true whether the graph is wighted or not

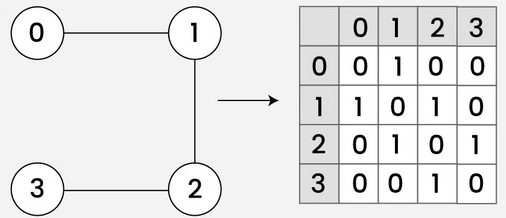
What is the adjacency matrix of this unweighted, undirected graph?

Notice the matrix is symmetric (imagine diagonal line from the top left-hand corner to the bottom right-hand corner)

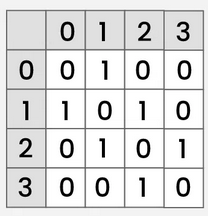
How are edges represented in the adjacency matrices of unweighted, directed graphs?

• 1 is set when an edge exists between two nodes

• 0 is set when there is no edge between two nodes

• A direction is chosen to represent edges directed away from a node. 

• In the image shown, each row represents the edges that are directed away from the node.

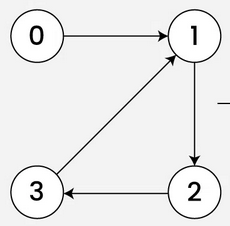
Is the data in an adjacency matrix for a directed graph symmetric?

• No

• This is true whether the graph is wighted or not

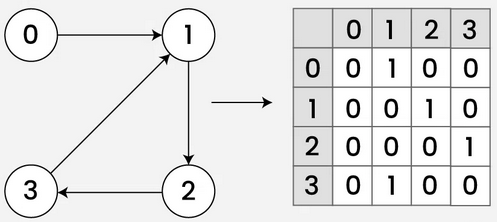
What is the adjacency matrix of this unweighted, directed graph, where each row represents the edges that are directed away from the node?

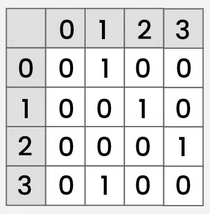
How are edges represented in the adjacency matrices of weighted graphs?

• The values of the weights are stored in the adjacency matrix (rather than just 1 or 0).

• If an edge does not exist between two nodes, a very large number (or often the infinity symbol, ∞) is set.

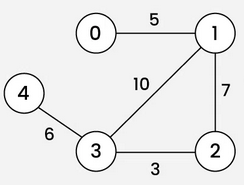
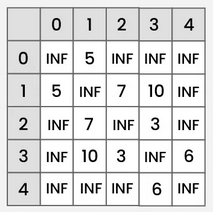
What is the adjacency matrix of this weighted, undirected graph?

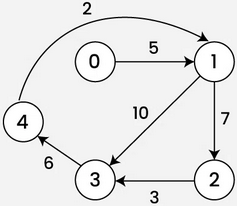
What is the adjacency matrix of this weighted, directed graph, where each row represents the edges that are directed away from the node?

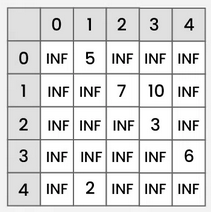
What is an adjacency list?

A list which records the existence of an edge between each node and all of its neighbours.

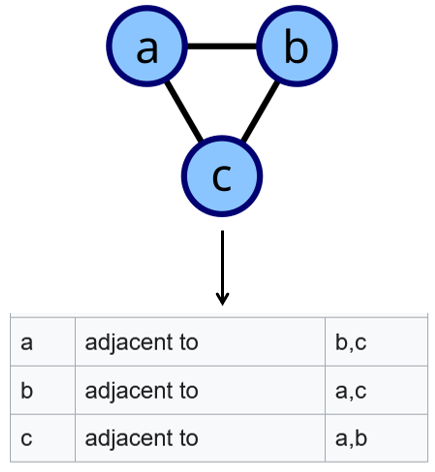
What does the adjacency list of a node contain in unweighted graphs?

The adjacency list of a node just lists each that node's neighbours.

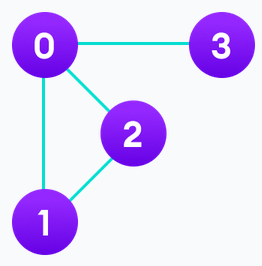
What is the adjacency list of this unweighted, undirected graph?

What does the adjacency list of a node contain in directed graphs?

The adjacency list of a node stores every neighbour of that node which has a directed edge from the node to the neighbour.

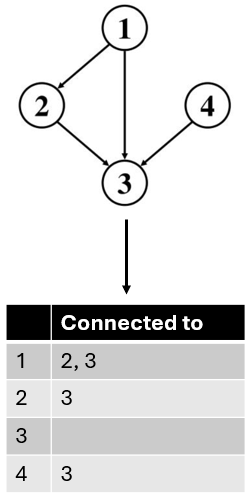
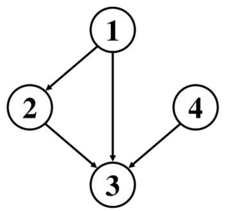
What is the adjacency list of this unweighted, directed graph?

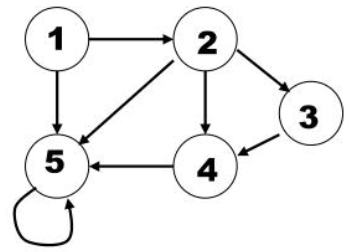
What is the adjacency list of this unweighted, directed graph?

What does the adjacency list of a node contain in weighted graphs?

The adjacency list of a node stores connections between two nodes, and the corresponding weights

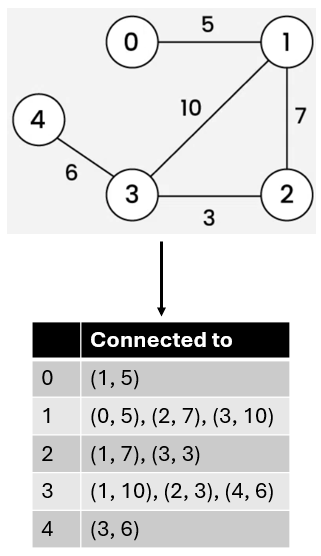
What is the adjacency list of this weighted, undirected graph?

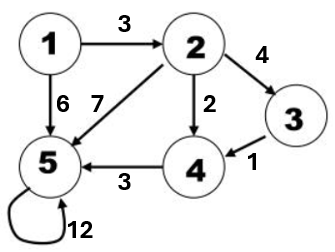
What is the adjacency list of this weighted, directed graph?

What are the advantage(s) of adjacency matrices?

• Finding data within the matrix is very time efficient, because the edge data is held in cells (intersections of rows and columns) that can be accessed directly by index.

• Offers a better time complexity than adjacency lists for removing edges

What are the disadvantage(s) of adjacency matrices?

• Adding and deleting nodes has a worse time complexity than adjacency matrices

What are the advantage(s) of adjacency lists?

• They are space efficient for graphs with few edges (sparesely populated graphs)

• Offers a better time complexity than adjacency matrices for adding and deleting nodes

What are the disadvantage(s) of adjacency lists?

• Determining the presence (or absence) of an edge will require a linear search (through the list of adjacent neighbours)

• Removing edges has a worse time complexity than adjacency matrices