biomechanics final

isotropic

materials that have UNIFORM properties in ALL directions

isotropic: stress and strain dimensions

3D

isotropic: stress/strain units

stress (Pa), strain (dimensionless)

orthotropic

materials that have DIFFERENT properties in 3 mutually perpendicular directions

orthotropic: stress and strain dimensions

3D

orthotropic: stress/strain units

stress (Pa), strain (dimensionless)

Vector Algebra: solve for magnitude of P1 + P2

P1 = (3i + 3j - 5k) P2 = (-2i + 3j + 10k)

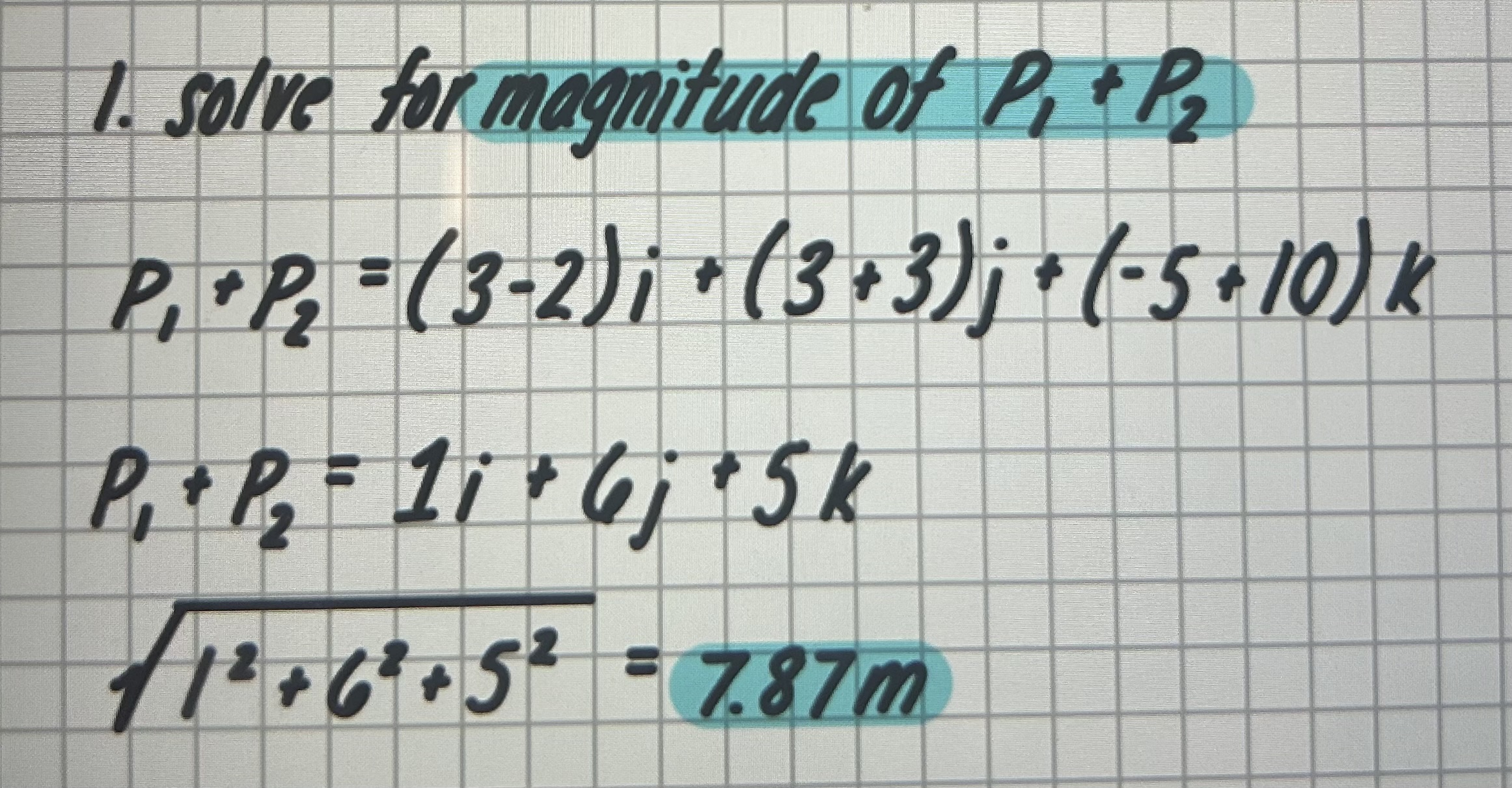
Vector Algebra: solve for angle between P1 and P2

P1 = (3i + 3j - 5k) P2 = (-2i + 3j + 10k)

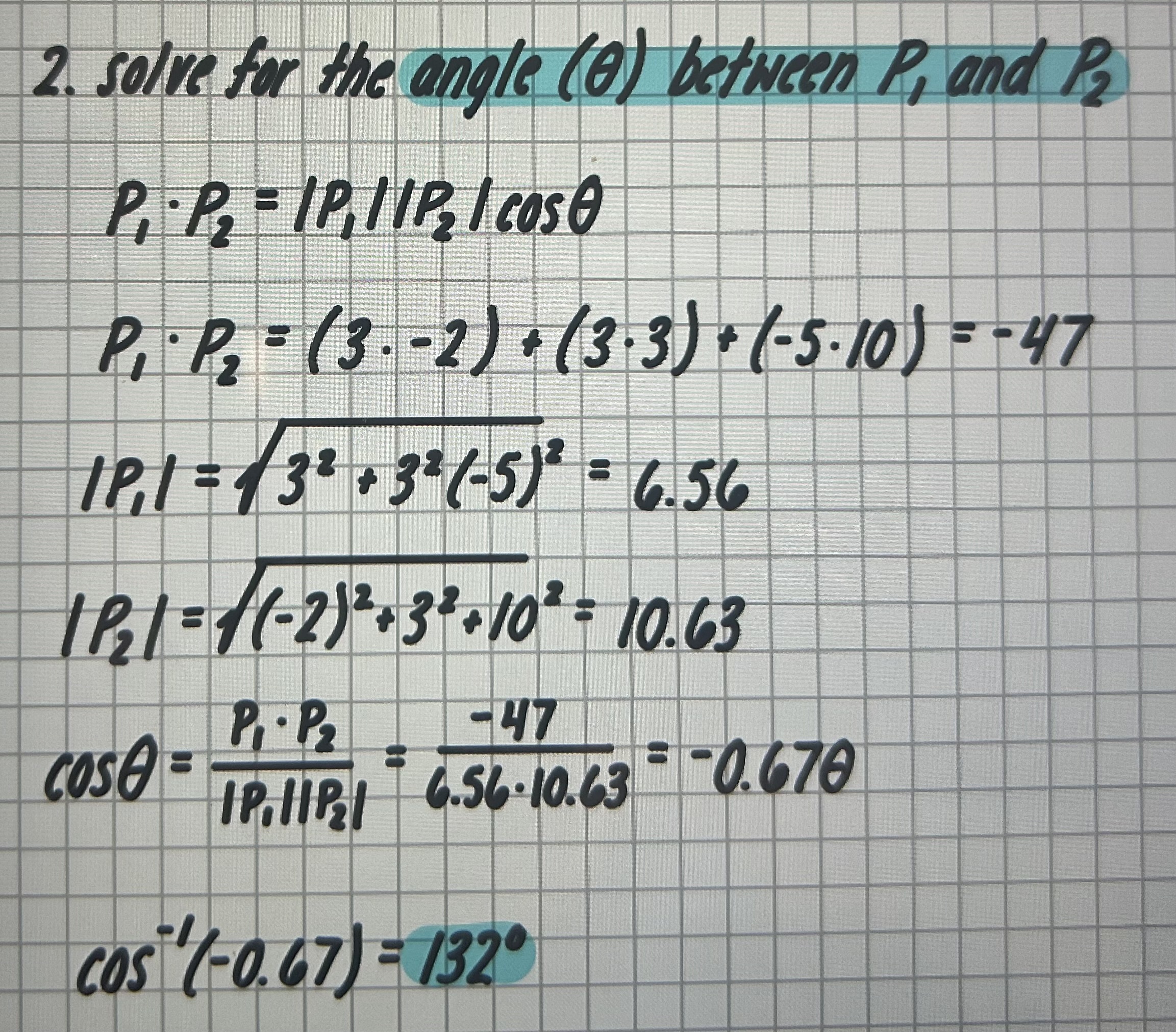
Vector Algebra: what is unit vector (in Cartesian form) associated with P1

P1 = (3i + 3j - 5k) P2 = (-2i + 3j + 10k)

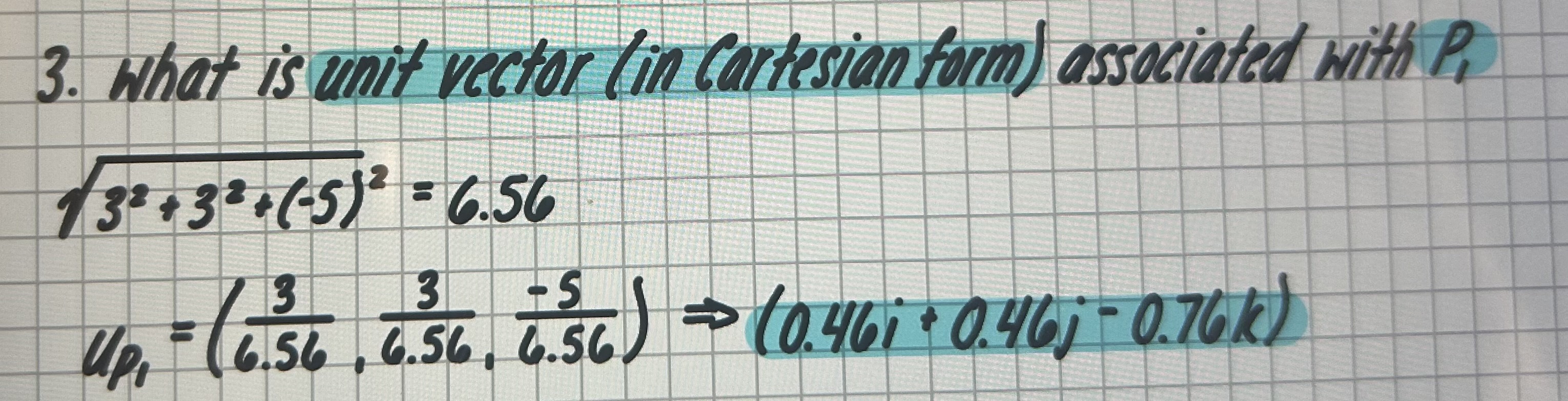
Vector Algebra: what is unit vector that is normal to the plane that contains P1 and P2

P1 = (3i + 3j - 5k) P2 = (-2i + 3j + 10k)

Vector Algebra: what is angle between P1 and positive x-axis

P1 = (3i + 3j - 5k) P2 = (-2i + 3j + 10k)

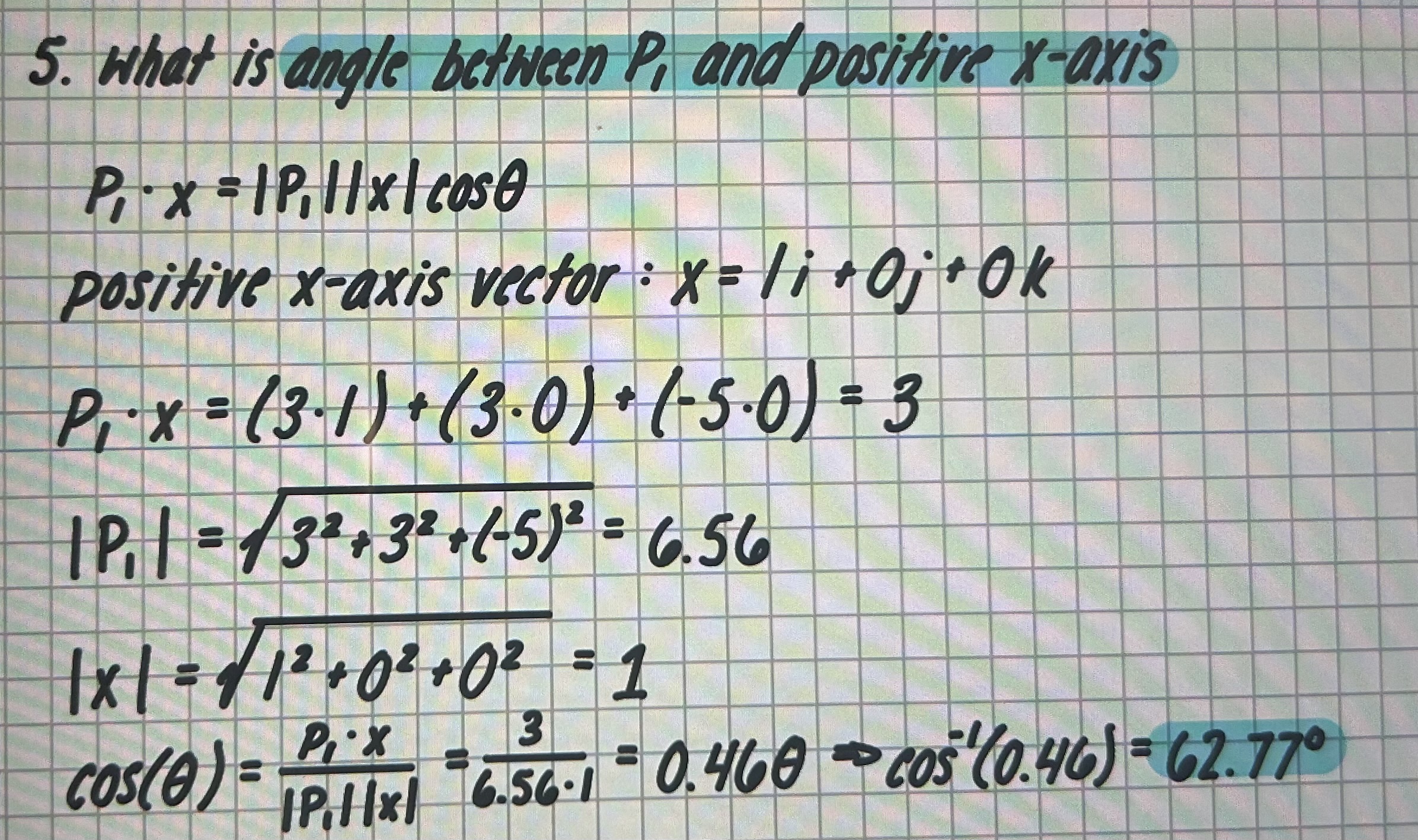
Thick-walled cylinder

circumferential stress (sigma theta,theta) varies in a thick-walled cylinder with radius r

• typically given by formula in picture where A and B are constants determined by boundary conditions

average circumferential stress process

1. integrate sigma theta, theta (r) over radial distance from ri to ro (inner to outer)

2. divide by length of the interval

Thin-walled cylinder

circumferential stress is assumed to be UNIFORM and can be approximated by formula in picture

• p: internal pressure

• ri: inner radius

• t: wall thickness

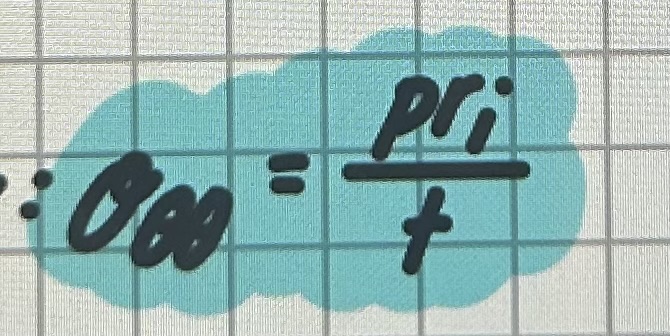
compare thick-walled vs thin-walled averages

to compare need to evaluate the integral for the thick-walled cylinder and see if it matches the thin-walled approximation

practice example for thick vs thin-walled average comparison

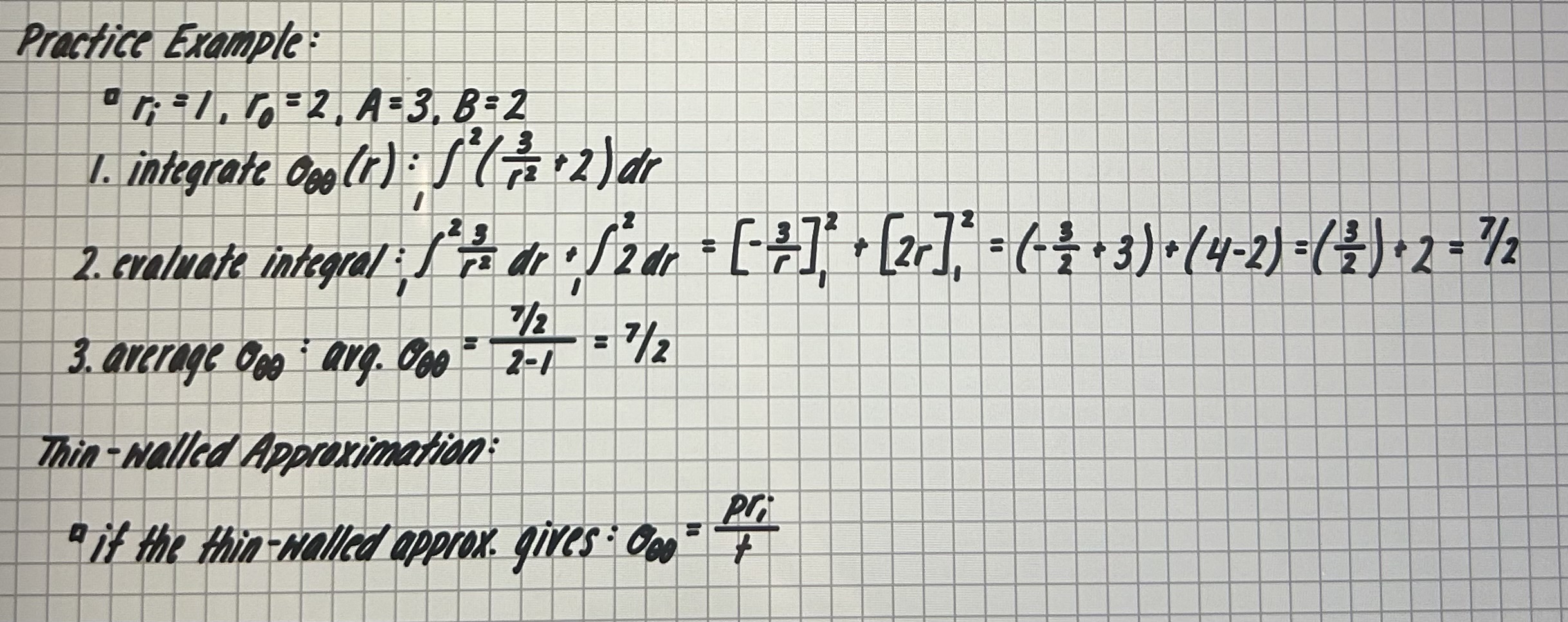
continuum hypothesis

• treats ALL properties and variables as continuous smooth mathematical functions

• ALL properties and variables are DIFFERENTIABLE

Hooke’s Law

• describes relationship between stress and strain in elastic materials

  • strain in a material is proportional to the applied stress within elastic limit of the material

stress

• Pa or N/m²

• stress is force applied per unit area within materials

Modulus of Elasticity (E)

• Young’s Modulus

• Pa

• measure of stiffness of a material

strain

• no units

• deformation or displacement of material relative to its original length

normal/shear stresses

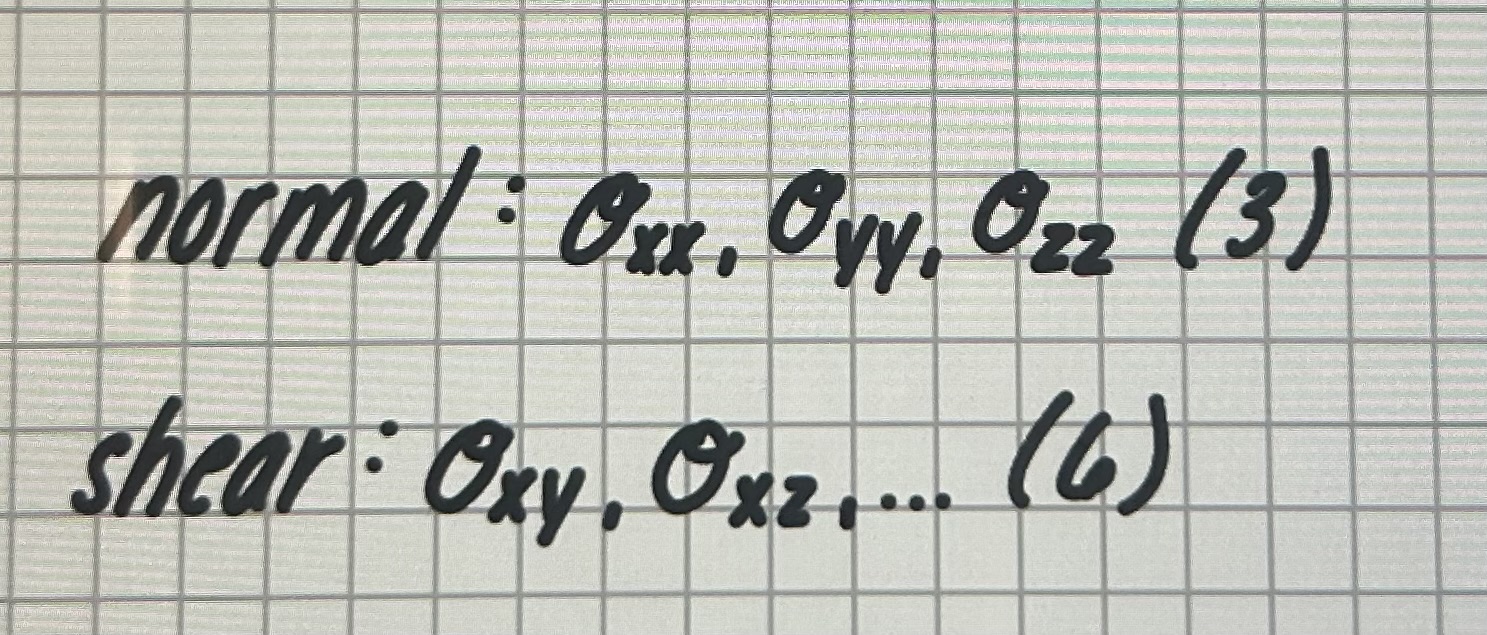
draw a principal stress

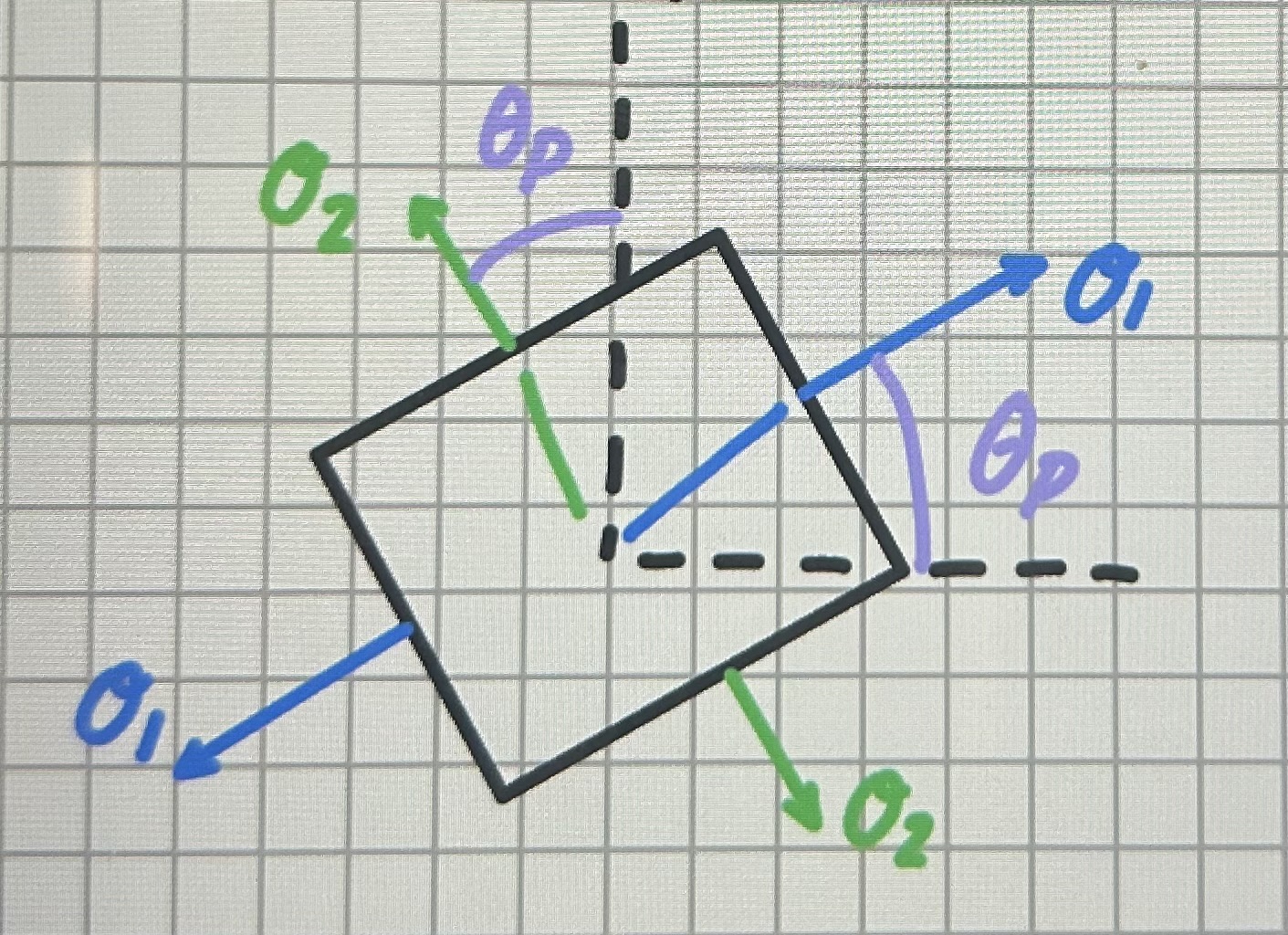
what tensor is a principal stress

• 2nd order tensor

• scalar

  • normal stresses on principal planes (no shear)

describe 2 reasons why you use Eularian acceleration in fluid mechanics

1. convective acceleration

2. local acceleration

convective acceleration

change due to movement through fluid

• in steady flow

local acceleration

time-rate of change at a fixed point

• unsteady flow

Derivation of Eularian Acceleration

Eularian

focuses on FIXED POINTS in space and observes how MATERIAL FLOWS PAST THEM

• ex. watching water pass a buoy

Lagrangian

tracks INDIVIDUAL PARTICLES or MATERIAL POINTS as they move through space and time

• ex. watching a swimmer

Derivation for thin-walled cylinder with pressure (closed ends)

For universal solutions, are stresses the same across different materials

No

• universal solutions must account for SPECIFIC MECHANICAL PROPERTIES (stress response of materials under load)

constitutive equations

force displacement relationship depending on conditions of interest or stress and strain

FBD for only equilibrium

No

• used for both equilibrium/non-equilibrium context problems

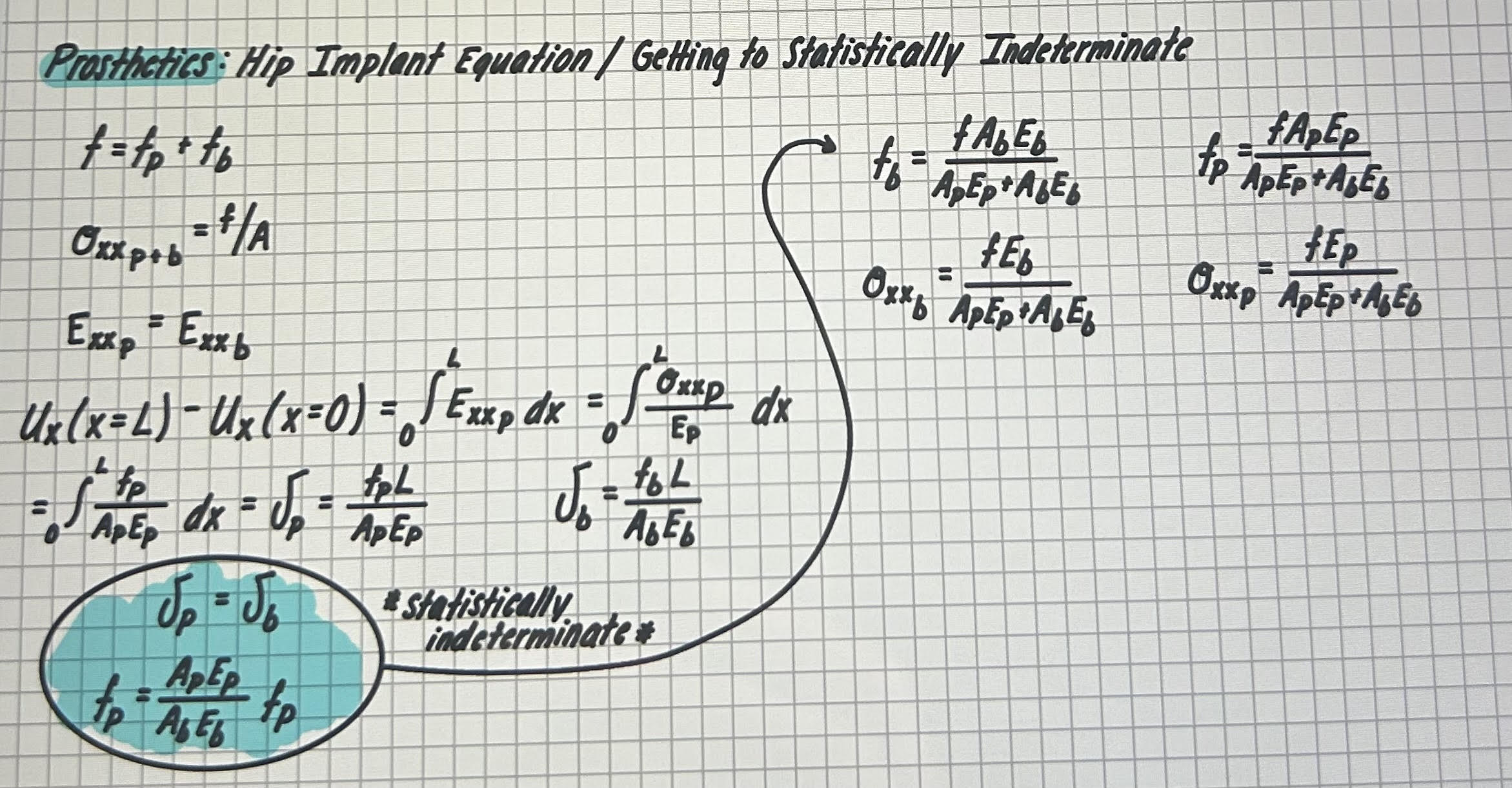
Prosthetic Hip Implant