function transformations SUPER IMPORTANT FOR GRAPHING EVERY THING TRIG TO

PHASE SHIFT

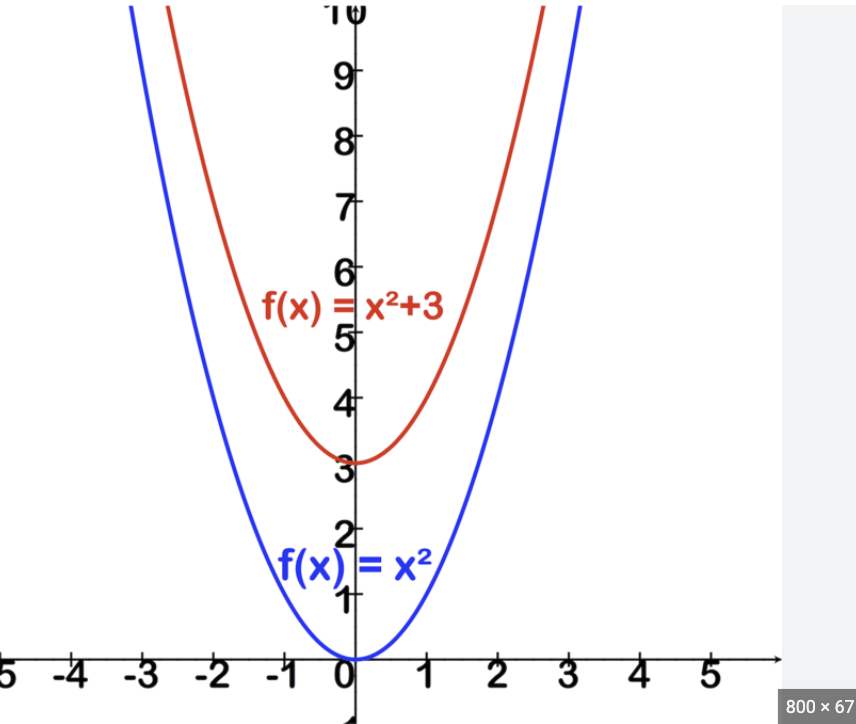
vertical shift

y=f(x)+d upward

f(x)-d downward

Shifting the graph verticaly d units

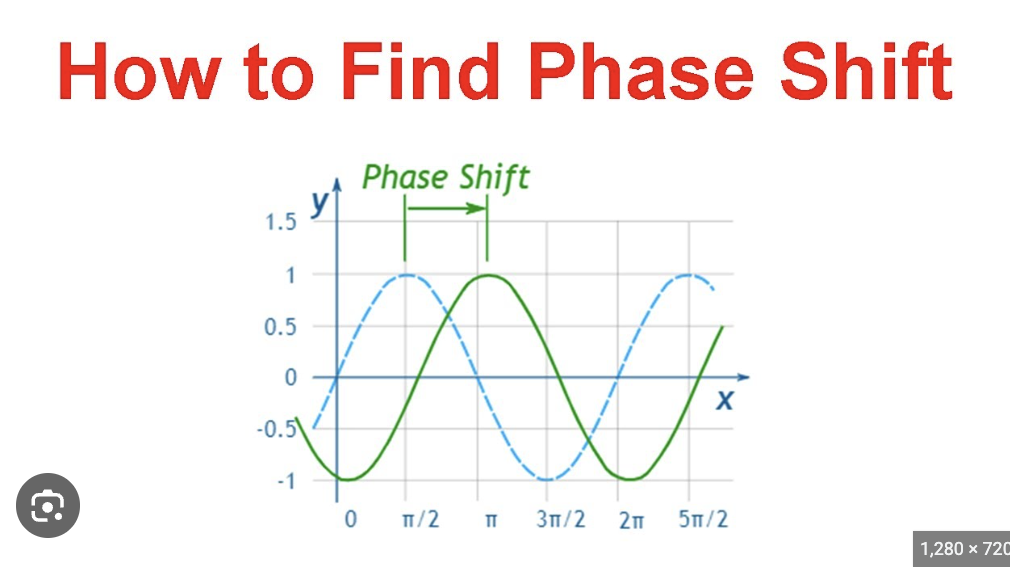
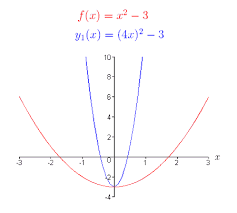
horizontal shift/ PHASE SHIFT SUPER IMPORTANT

example using trig

y = a sin (bx + c) + d

to get the horizontal shift which is

f(bx+c) you have to SET EQUAL TO ZERO AND SOLVE FOR X

bx+c=0

bx=-c

and then divide by B

get the PHASE SHIFT AS -C/B

You can also do it with normal functions

y=3(-x/3+1)²+2

set parenthesis equal to 0 and

-x/3+1=0

and get x= -3 so shift 3 units to the left

(left if c/b is positive, right if negative).

reflection on the y axis and reflection over x-axis

y=f(-x) Reflection over y-axis Reflection over y-axis is inside of the Parenthesis

y=-f(x) Reflection over x-axis Reflection over x-axis outside of parenthesis

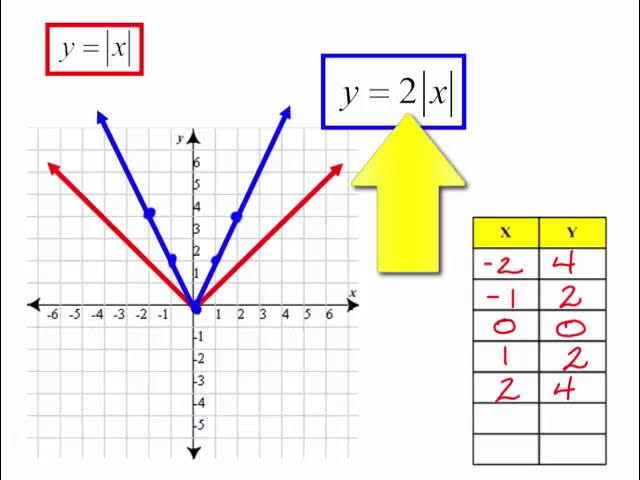
Vertical stretch

af(x), where a>1. Vertical stretch by A away from the x-axis

So outside of the parenthesis and greater than 1

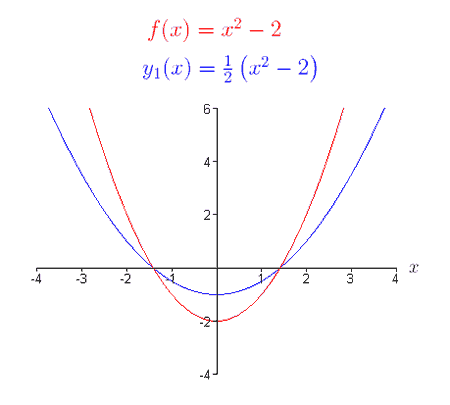
Vertical Shrink

af(x), where 0<a<1.  Vertical shrink by 1/a toward the x-axis 

So outside of the parenthesis and less than one but greater than 0 because negative is a reflection

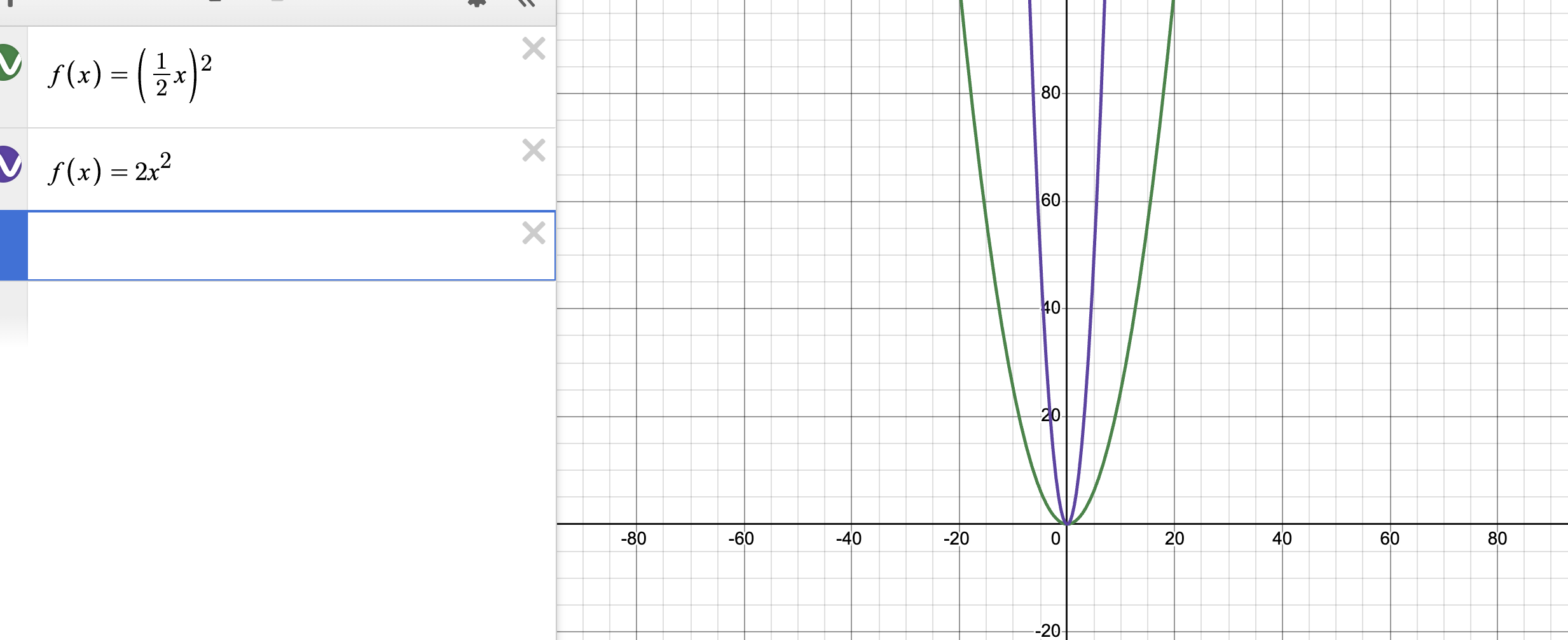
HARDEST PART IS HORIZONTAL STRETCH WEIRD PART ABOUT THEM

Horizontal Stretch different than VERTICAL

f(ax), where 0<a<1. Horizontal stretch by 1/a away from the y-axis

Horizontal Shrink different than VERTICAL

f(ax) where a>1 Horizontal shrink by 1/a toward the y-axis

Why horizontal stretch and shrink different than vertical shrink and stretch

• Vertical transformations affect the output (y-values) directly.

  • Stretch: Multiply the whole function by a number > 1 → graph gets taller.

    • Example: y=2f(x)y = 2f(x)y=2f(x) → y-values double.

  • Shrink: Multiply by a number between 0 and 1 → graph gets shorter.

    • Example: y=0.5f(x)y = 0.5f(x)y=0.5f(x) → y-values cut in half.

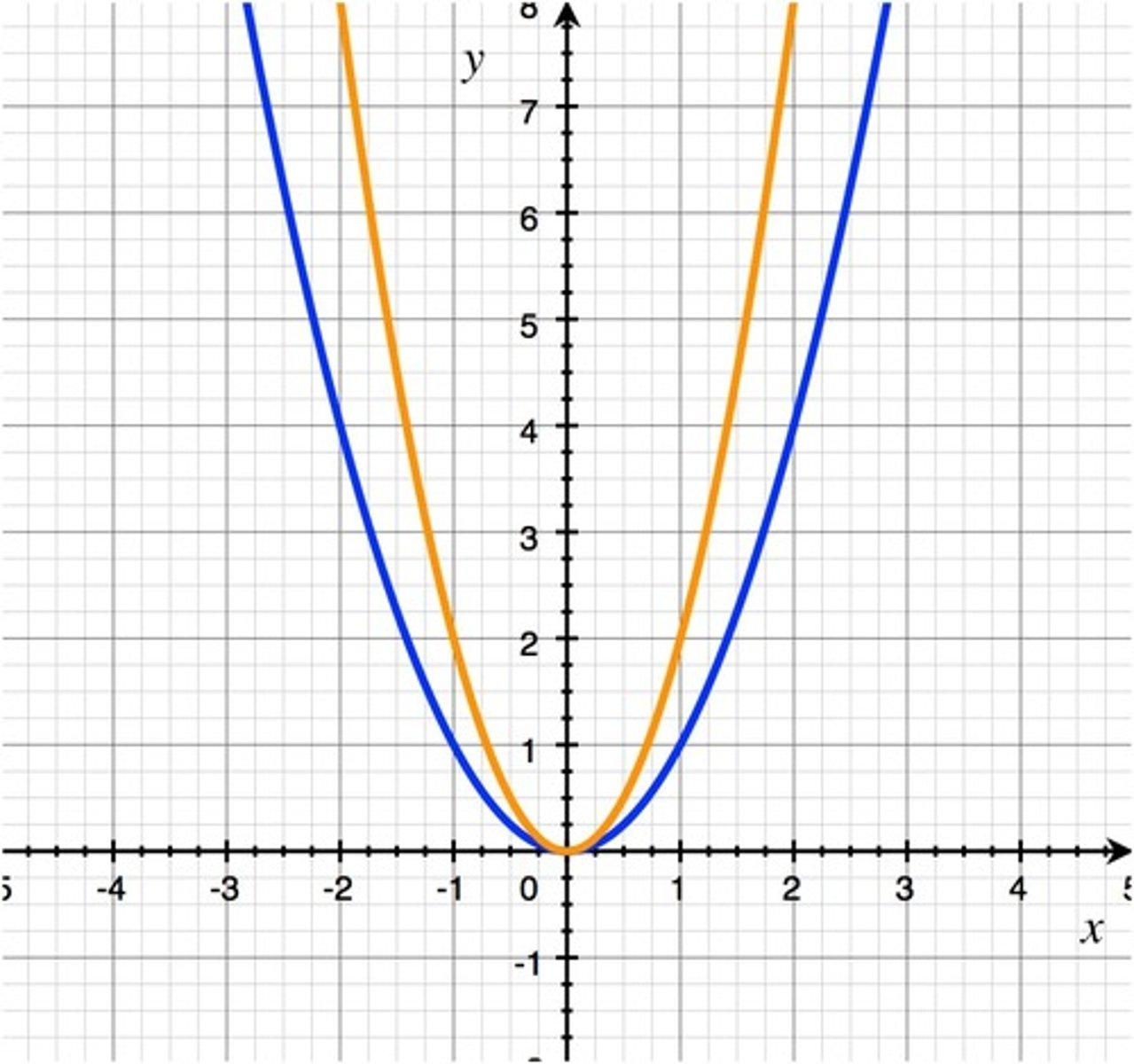
• Horizontal transformations affect the input (x-values) inside the function.

  • Shrink: Multiply x by a number > 1 → graph grows faster → graph gets “skinnier.”

    • Example: y=f(4x)y = f(4x)y=f(4x) → smaller x-values reach the same y.

  • Stretch: Multiply x by a number between 0 and 1 → graph grows slower → graph gets “wider.”

    • Example: y=f(0.5x)y = f(0.5x)y=f(0.5x) → larger x-values needed to reach same y.

• Why they are opposite:

  • Vertical changes move the graph up/down directly.

  • Horizontal changes move the graph left/right by changing how fast you reach the same y-values.

  • So a big number outside = taller (stretch), but a big number inside = faster growth → compressed (shrink).

x-axis

y=0

y-axis

x=0

Translation

A shift of a graph horizontally, vertically, or both, which results in a graph of the same shape and size, but in a different position.

Reflection

A flipping of graph of a function across a horizontal or vertical line that results in a graph with the same shape and size.

In an exponential function, f(x)=A*b^(Bx-C)+D, this value determines how far the graph shifts left and right.

C-value

In an exponential function, f(x)=A*b^(Bx-C)+D, this value determines how far the graph shifts up and down.

D-value

In an exponential function, f(x)=A*b^(Bx-C)+D, when this value is negative, the graph reflects across the x-axis.

A-value

In an exponential function, f(x)=A*b^(Bx-C)+D, when this value is negative, the graph reflects across the y-axis.

B-value

Write the function notation for the transformation from the parent function

f(x)=2^(x-3)

f(x-3)

Write the function notation for the transformation from the parent function

f(x)=2^(x+3)-2

f(x+3)-2

Write the function notation for the transformation from the parent function

f(x)=2^(x-3)+2

f(x-3)+2

Write the function notation for the transformation from the parent function

f(x)=2^(x)+2

f(x)+2

Write the function notation for the transformation from the parent function

f(x)=2^(-x-3)

f(-x-3)

Write the function notation for the transformation from the parent function

f(x)=-2^(x-3)

-f(x-3)

Write the function notation for the transformation from the parent function

f(x)=-2^(x)-2

-f(x)-2

Write the function notation for the transformation from the parent function

f(x)=-2^(x)+2

-f(x)+2

Write the function notation for the transformation from the parent function

f(x)=-2^(x+3)+2

-f(x+3)+2

Write the function notation for the transformation from the parent function

f(x)=2^(-x+3)+2

f(-x+3)+2

Write the function notation for the transformation from the parent function

f(x)=2^(-x-3)+2

f(-x-3)+2