Parties 1 et 2 (transfert thermique et principes de la thermo + équation de la diffusion thermique)

dans quel sens se fait le transfert thermique ?

Du corps le plus chaud vers le corps le plus froid pour homogénéiser les températures

transfert par conduction (définition)

• transfert thermique possible seulement dans les solides

• sans transport macroscopique de matière

transfert par convection (def)

• avec transport macroscopique de matière

• domine souvent la convection dans les fluides

transfert par rayonnement (def)

• dû à la température du matériau

• se fait sans transport de matière (possible dans le vide de l’espace par exemple)

premier principe de la thermodynamique

avec :

• E_m = E_c + E_p l’énergie mécanique du système

• Q le transfert thermique de l’extérieur vers le système

• W le travail reçu par le système ( W = -P_ext∆V lorsque l’évolution est monobare)

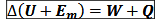
Second principe de la thermodynamique

∆S = S_échangée + S_créée avec : 

• S_échangée = Q/T_ext

•  S_créée ≥ 0

Version infinitésimale des 2 principes

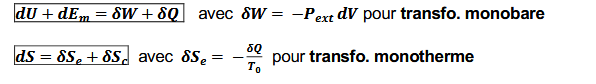
différence entre d et δ

• d est réservé aux variations d’une variable d’état ou fonction d’état, qui ne dépend pas du chemin suivi lors des transformations élémentaires

• δ s’applique à une grandeur qui n’est pas une fonction d’état, donc dépend du chemin suivi et n’est pas défini au cours des transformations

unité du vecteur densité thermique j_Q

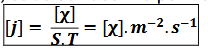
vecteur densité de courant (définition)

quantité de X qui traverse une surface par unité de temps et de surface

Quand apparait un transfert thermique par conduction ?

Quand il y a présence d’une inhomogénéité de température dans un milieu matériel sans mouvement macroscopique

Propriétés de ce transfert thermique par conduction ?

• la diffusion thermique cesse lorsque la température est homogène => j_Q^→ doit s’annuler lorsque le gradient de température est nul

• transfert thermique orienté des zones de température élevée vers les zones de température faible => j_Q est orienté selon les températures décroissantes, càd dans le sens inverse du gradient de température

• relation de linéarité entre le gradient de température et le vecteur densité thermique

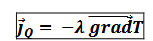
Loi phénoménologique de Fourier

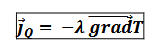
conductivité thermique λ (définition)

capacité du milieu à conduire le flux thermique

loi phénoménologique (définition)

elle est déduite de l’expérience et n’a pas de caractère universel. Elle s’applique dans un cadre limité

conductivité thermique de l’eau

λ = 0.6 W.K^-1.m^-1

conductivité thermique de l’air

λ = 2.10^-2 W.K^-1.m^-1

conductivité thermique du cuivre

λ = 4.10² W.K^-1.m^-1

conductivité thermique du bois

λ = 0.6 W.K^-1.m^-1

conductivité thermique des métaux bons conducteurs

λ ≈ 10² W.K^-1.m^-1

conductivité des métaux médiocres conducteurs électriques

λ ≈ 10 W.K^-1.m^-1

conductivité béton, verre, eau

λ ≈ 1 W.K^-1.m^-1

conductivité thermique de laine de verre, air

λ ≈ 10^-2 W.K^-1.m^-1

analogie entre la conduction électrique et la conduction thermique

équation locale du bilan énergétique

• j_Q le vecteur densité de courant thermique

• µ la masse volumique en kg.m^-3

• c la capacité calorifique massique en J.K^-1.kg^-1

• P_th la puissance thermique, appelée terme source de l’équation

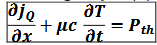
généralisation en géométrie quelconque de l’équation locale du bilan énergétique

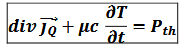
Laplacien (définition)

• ∆ : opérateur laplacien

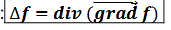
opérateur divergence (définition)

gradient (définition)

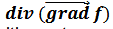
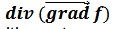
∆f = 

se retrouve en composant les opérateurs gradient et laplacien

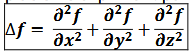
équation pilote de la diffusion thermique

se retrouve en : 

• appliquent la loi de Fourier : jth^→ = -λgrad^→T

• remplacer j_th par son expression à l’aide de la loi de Fourier dans l’équation du bilan d’énergie

• composer le gradient et le divergent pour faire apparaitre le laplacien

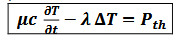
équation pilote sans le terme source

• avec D_th =

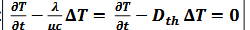
diffusivité thermique ou coefficient de diffusion

D_th = λ/µc

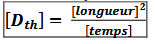
diffusivité thermique pour un solide bon conducteur

D ≈ 10^-4 m².s^-1

diffusivité thermique d’un solide mauvais conducteur

D ≈ 10^-7 m².s^-1

diffusivité thermique d’un fluide

D ≈ 10^-5 m².s^-1

• L : taille de l’objet en unité de longueur

• D_th la diffusivité thermique

• τ la durée du transfert thermique

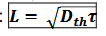
relation entre les variations dans l’espace et dans le temps 

les variations dans l’espace et dans le temps sont dissymétriques

conséquence de cette dissymétrie sur les phénomènes diffusifs

• la diffusion est plus efficace aux temps courts ou pour des petites échelles spatiale

• elle s’essouffle aux temps longs

• dans les gaz et liquides, les phénomènes diffusifs vont rapidement être masqués par la convection à grande échelle spatiale

irréversibilité temporelle de la diffusion thermique 

L’équation de diffusion (contrairement à l’équation d’Alembert de propagation),

n’est pas invariante par renversement du temps

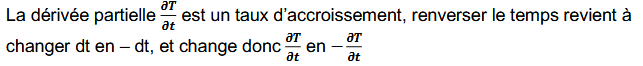
conditions aux limites (définition)

contraintes sur les variables spatiales à la frontière du système (surface extérieure)

conditions aux limites pour un contact entre deux solides sans flux imposé

température continue à l’interface => T₁ = T₂ 

cela est pour éviter que le flux thermique mettant en jeu des dérivées spatiales ne diverge sur la frontière

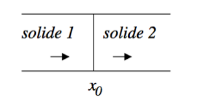
condition de contact thermique parfait

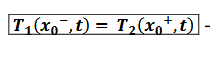
égalité des flux thermiques à l’interface

se retrouve en calculant le flux thermique de chaque côté de l’interface et en égalisant les deux expressions

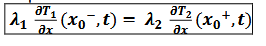
contacte entre deux solides avec flux imposé

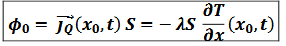
si la paroi est calorifugée, que peut-on dire de 𝝏𝑻/𝝏𝒙 ?

une paroi calorifugée impose la nullité de la composante normale du vecteur densité de courant (j_Q^→.n^→ = 0)

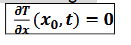
loi de Newton exprimant le courant conducto-convectif (cc) au voisinage de l’interface solide/fluide

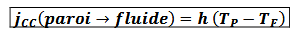
équivalent de la loi phénoménologique de Newton en fonction de Q_cc

se retrouver en calculant δQ_cc = Φ_ccdt puis en remplaçant Φ_cc par sa définition en fonction de j_cc et dS (Φ_cc = ∫∫_S (j_ccdS), puis on intègre cette relation et remplace le tout dans δQ_cc = Φ_ccdt

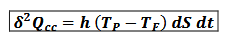
coefficient conducto-convectif h (unité)

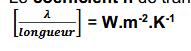
de quoi dépend la valeur du coefficient conducto-convectif h

• nature du fluide

• épaisseur de la couche limite

• viscosité du fluide

ordre de grandeur du coefficient conducto-convectif h

• plus élevé pour un liquide : h > 100 W.m^-2.K^-1

• plus bas pour un gaz : h ≈ 10 W.m^-2.K^-1

• plus la convection est intense, plus h augmente

dans le cas de l’ailette de refroidissement, quelle est l’équation différentielle qui pilote l’évolution de la température (en régime stationnaire) ?

avec :

• L : distance caractéristique

• T : la température en fonction de la position

• T_e : la température extérieure

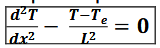
expression de la distance caractéristique L

L² = λR/2h avec : 

• R : le rayon de la surface

• λ : 

• h : coefficient conducto-convectif

expression du profil de température dans le cas d’une ailette de refroidissement (en régime stationnaire)

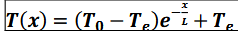
flux de conduction entrant pour l’ailette de refroidissement

se retrouve en calculant  Φ_e = ∫∫_S j_diff(x=0).dS qui nous donne le flux qui entre en x = 0

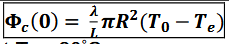
En l’absence d’ailette, le flux conducto-convectif évacué par une le disque de rayon

R est :

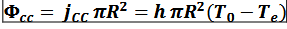
résumé des conditions aux limites