HSC 405: Unit 2: Stability/Static Equilibrium/ Angular Kinematics

External Moment Arm from Weight Machine

- external mA changes as machine angle changes (force stays the same, but Torque changes bc of moment arm)
- most muscle moment arms change as the joint angle changes + this results in varying torque producing capabilities
- many machines try to match the muscle torque producing capability to require constant muscle effort throughout the range of motion

center of gravity (center of mass)

the point in a body or system around which its mass or weight is evenly distributed or balances and through which the force of gravity acts
- human body COG= 1-2 inches below your navel

stability

- the capacity of an object to return to equilibrium or to its original position after it has been displaced
- affected by the position of an object's center of gravity above the ground + relative to the edges of the support base (heavier objects are inherently more stable than lighter objects)

base of support

the area within the lines connecting the outer perimeter of each of the points of support

factors that influence stability

- height of the center of gravity
- weight of the object
- size of the base of support

stability increases

- as the center of gravity is lowered
- if the object is moved farther from any edge of the base of support

are taller people less stable than short people?
does a cane increase stability in a older person?
is a basketball player more stable when they squat?
is a football player in tandem stance more stable?

- yes; higher center of gravity
- yes; widens base of support (distributes weight over larger area)
- yes; lower center of gravity + widens base of support
- no; narrows base of support (less contact area with ground)

static equilibirum

- no additional forces or torques going into the system
- balanced; everything has to sum to 0
- not moving or moving at a constant velocity (no acceleration)

anthropometry

- science that discovers how much body parts weigh in term of body percentage

sagittal plane

- divides body into right and left halves
- creates a medial/lateral axis or a R/L axis
- allows for flexion and extension

frontal plane

- divides body into front and back sections
- creates anterior/posterior axis
- allows for abduction and adduction

transverse plane

- divides body into superior and inferior segments
- creates a superior/inferior axis
- allows for internal and external rotation

plane

- a surface that is infinitely high, wide, + thin
- have to follow orientation of planes (around an axis; axis is always perpendicular to the plane)

Angular Kinematics

- everything moves about a fixed point (= axis of rotation) which is different than linear motion

Measuring angles

- 1 radian = 57.3 degrees
- 1 revolution = 360 degrees = 2π radians
- θ (degrees) = (180/π ) x θ(radians)

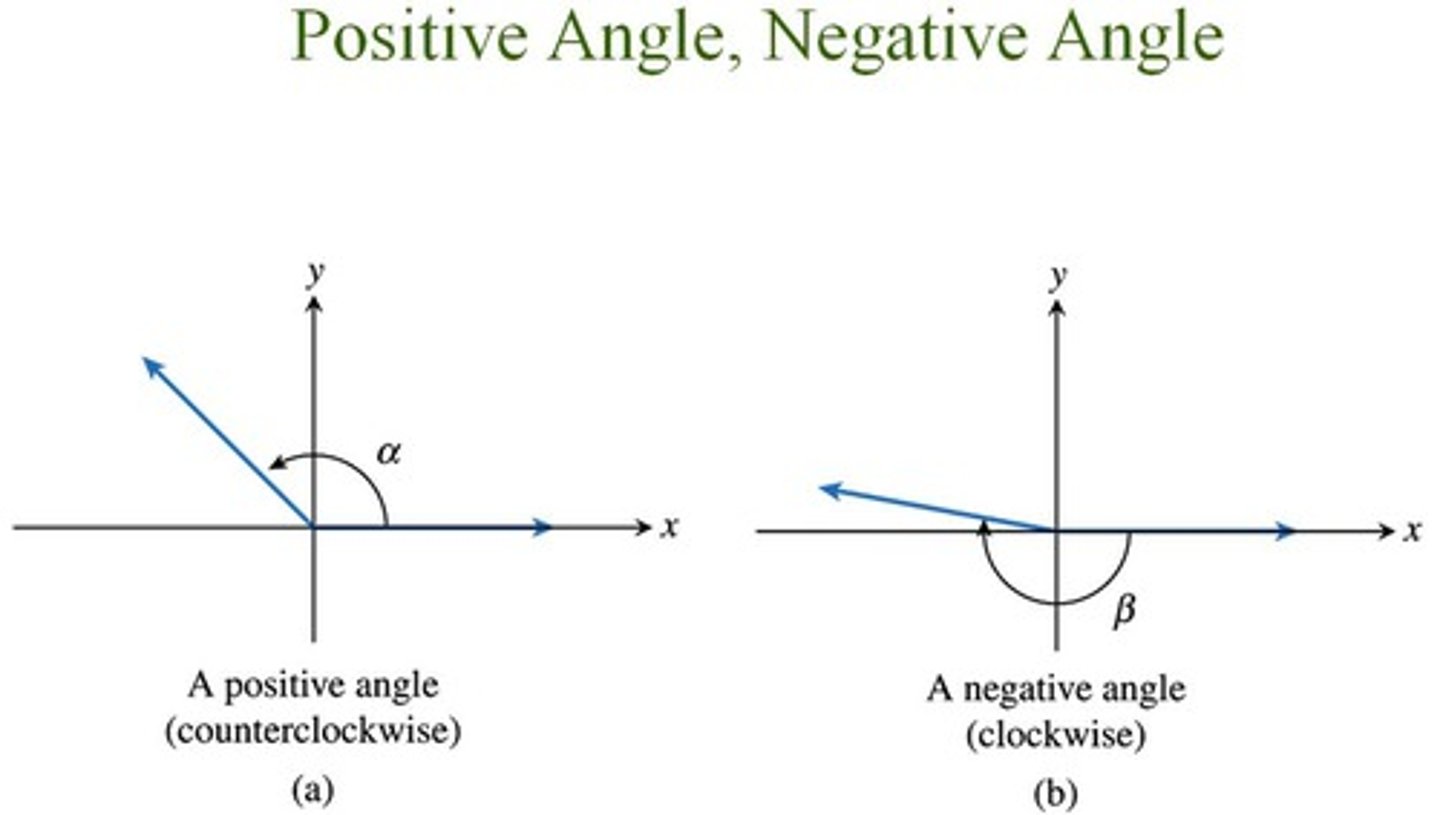
Positive vs Negative Angles

+ = CCW
- = CW

Angular Displacement

- change in the angle of an object or segment between 2 instants in time (final - initial)
- units = degrees/radians
- issue = don't know path = anything that happened in between

Angular Distance

- sum of the magnitude of all the changes in angle by rotating body
- units: degree/radians
- scalar (direction doesn't matter)

Angular Velocity

- rate of change of the angular position of an object
- equation: ω = θfinal - θinitial / tfinal - tinitial
- units: radian/s or degrees/s

Angular Speed

- the angular distance traveled divided by the time taken to cover it (scalar)
- equation: angular speed = angular distance/change in time
- units: radian/s or degrees/s
- angular speed cannot be smaller than angular velocity (distance is always greater than or equal to displacement)

Angular Acceleration

- the rate of change of angular velocity
- equation: angular acceleration = change in angular velocity / change in time
- units: rad/s^2 or degrees/s^2

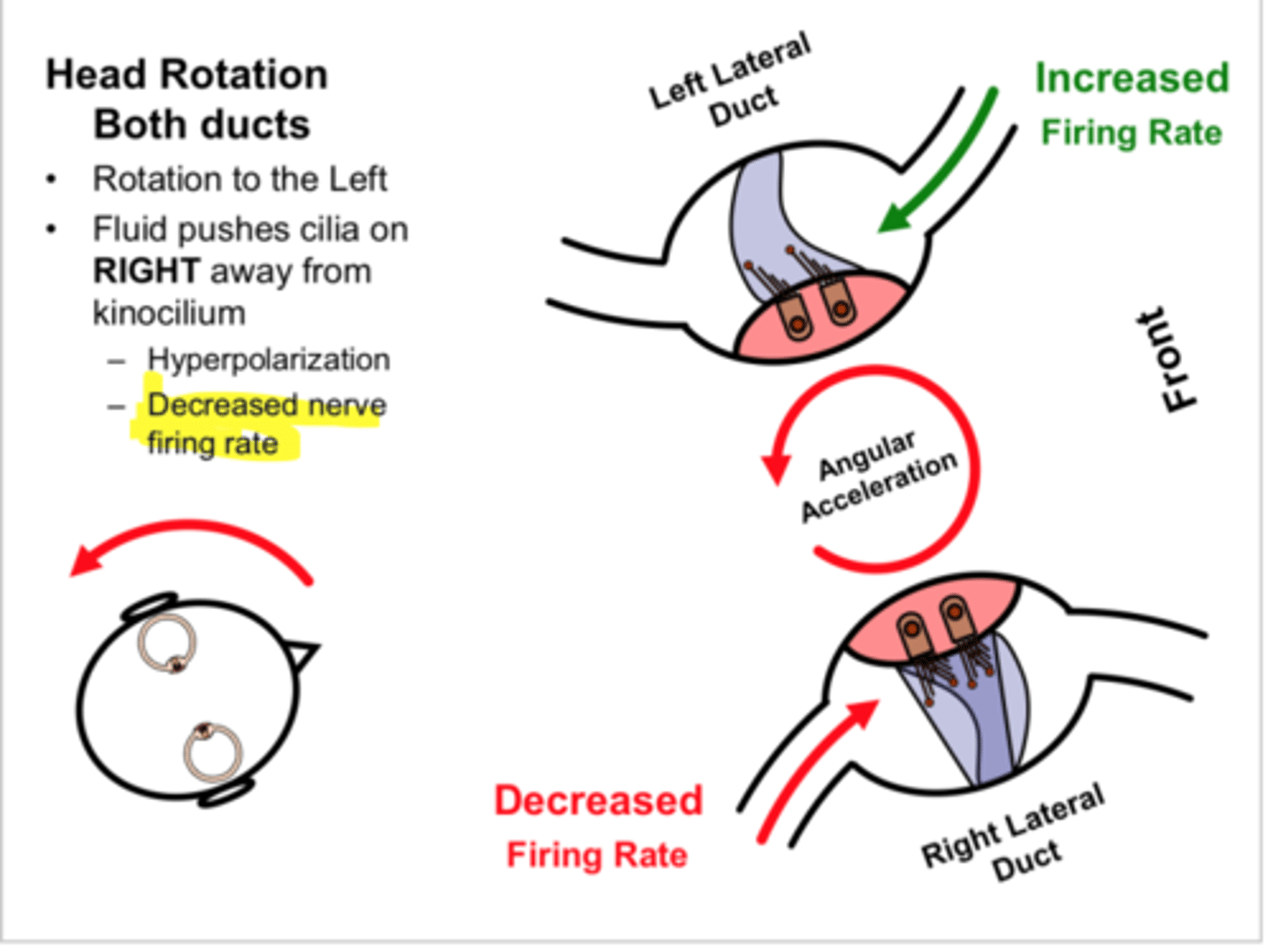
Effects of Angular Acceleration

- velocity and acceleration in the same direction: angular velocity increases
- velocity and acceleration in opposite directions = angular velocity decreases
- look at chart

propulsion

- speeding up (moving in the same direction as the muscle is pulling)
- when velocity and acceleration are both in positive or both in negative direction

breaking

- slowing down (acceleration is in the different direction as the motion)
- ex: top of motion of lifting arms up > triceps pull into extension to slow arms down (acceleration in opposite direction > eccentric movement)
- opposite directions (causes decrease in positive or negative direction)

can you list 2 factors at the time of release that influence the speed of a softball pitch?

- angular velocity: how fast you swing your arm
- radius of rotation: extending the elbow increases radius of rotation which will increase angular velocity

why is it easier to hit a home run off an outside pitch than an inside pitch?

- increased ROR > increased linear displacement > increased impulse (using more of bat so it takes more time to complete swing which increases impulse) > increased change of momentum (the longer you accelerate the faster your velocity becomes)

at what point in her spin does a discus thrower need to release the discus so that it will stay in bounds?

- has to release it somewhere behind her

why do distance runners typically run in the inside lane of a track, but sprinters prefer to run in lanes 3 or 4?

- lanes 3/4 = larger radius of rotation >> increased angular velocity >> sprinters can use the curves to help them run faster

Linear and angular rotation

the body uses angular motion to accomplish linear motion
- ex: gait, reaching, swinging a bat

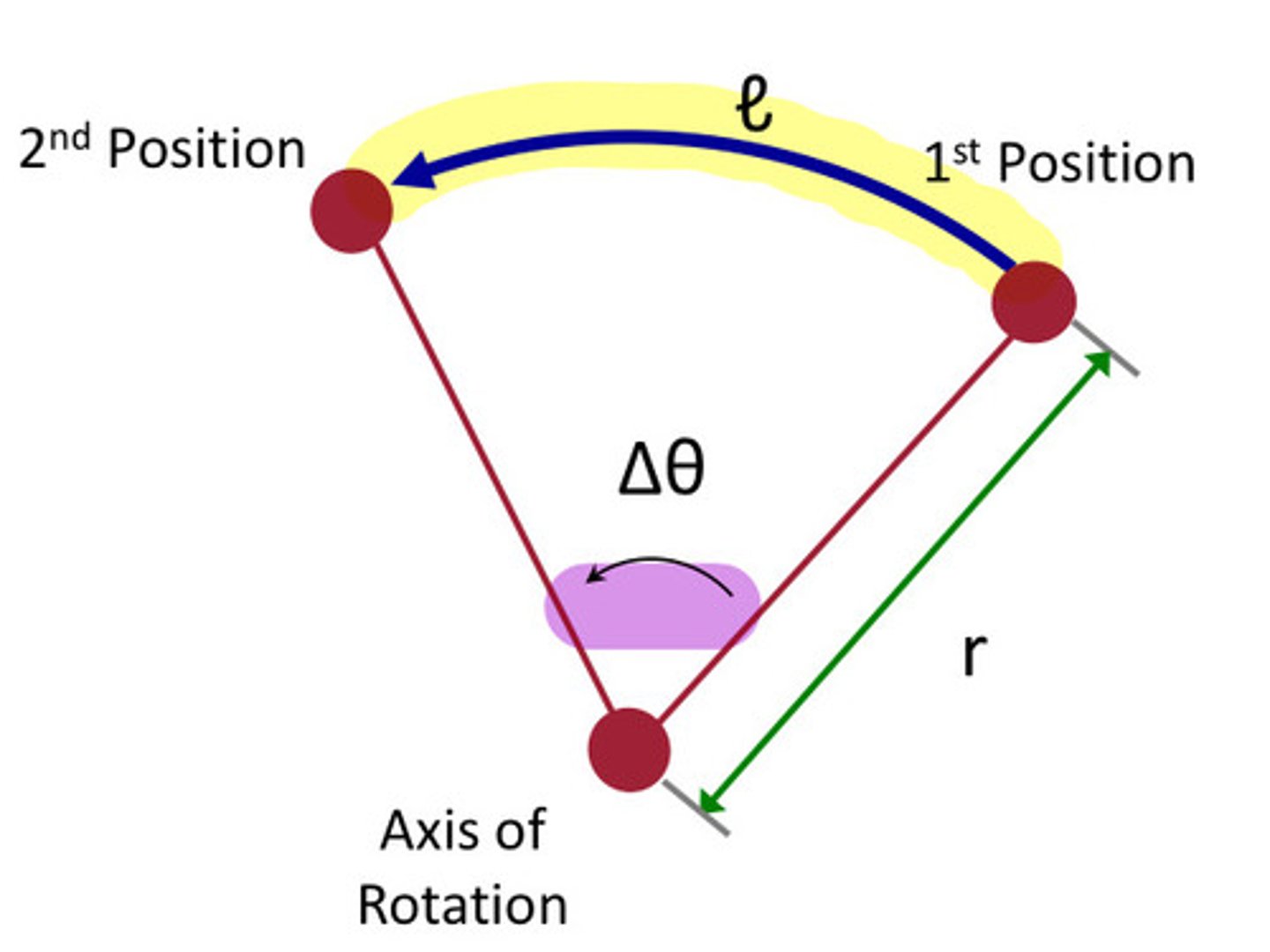
radius of rotation

- the distance from a point on a segment versus the axis
- the bigger the radius of rotation, the bigger the linear distance
- units: m/ft

curvilinear distance

- d = r|Δθ|
- units: m/ft

Linear and Angular velocity

- linear velocity is always tangential to the path of motion
- equation: v=rw
- w = radian/s

the greater the radius of rotation

- the greater the curvilinear distance (d) for a given change in angle + the greater the magnitude of linear velocity for a given angular velocity

Linear and Angular Acceleration

two components:
- tangential: along the path of motion
- radial: perpendicular to the path of motion

Tangential Acceleration

- acceleration along the path of motion
- produces a change in linear speed
- equation: aT = change in velocity / change in time
- if r is constant: aT= r (FIX)

Centripetal Acceleration

- acceleration towards the axis of rotation
- produces a change in direction
- equation: aR = v^2/radius
- equation if radius is constant: aR=rω^2

Most skeletal muscles in our limbs attach close to the joints. a. What are the advantages of this arrangement? b. What is the disadvantage of this arrangement?

a. Advantages of Close Muscle Attachments:
Muscles close to joints allow for increased limb range of motion and speed. When muscles contract to rotate a limb, their attachment point moves through a small arc length, while the limb's distal end moves through a larger arc length. This proximity to the joint allows for sufficient muscle stretch and contraction, enabling a wide range of motion. Additionally, the longer radius of the distal limb compared to muscle attachment sites results in faster linear velocity, enhancing speed.
b. Disadvantage of Close Muscle Attachments:
Close muscle attachments mean shorter moment arms, requiring muscles to generate large forces for relatively small torques around a joint.

In golf, the longest club is the driver, and the shortest club is the pitching wedge. Why is it easier to hit the ball farther with a driver than with a pitching wedge?

If the two clubs can be swung with the same angular velocity, then the longer swing radius of the driver will cause a faster linear velocity of the club head according to the relationship v = ωr.

3. What advantages does a longer-limbed individual have in throwing and striking activities?

Besides having the ability to do greater work due to greater displacement (see review question 4 in chapter 4), a longer-limbed individual has a longer swing radius, which may cause a faster linear velocity at the end of the limb according to the relationship v = ωr.

4. Explain how step length (a linear kinematic variable) might increase if flexibility exercises increase the range of motion at the hip joint, thus increasing the angular displacement (an angular kinematic variable) of the hip joint during a step.

The angular displacement of the leg during a step is related to the linear distance traveled by the foot during a step (which is related to the step length) as shown in the following equation: Arc length = θr

5. Why is sprinting around a curve in lane 1 (the inside lane) more difficult to do than sprinting around the curve in lane 8 (the outside lane)?

It is more difficult to run fast in lane 1 because your centripetal acceleration is greater due to the smaller radius of lane 1 compared to lane 8. This means that you must generate greater frictional forces under your feet in the radial direction to cause your centripetal acceleration.

6. What is the plane of motion for most of the joint actions that occur during sprint running? What is the corresponding axis of motion for these joint actions?

Sagittal plane and transverse axis

7. When you swing a baseball bat, what is the plane of motion for the action occurring at your leading shoulder? What is the axis of motion? What joint action occurs at the leading shoulder during the swing?

Horizontal abduction (or horizontal extension) in the transverse plane around a longitudinal axis

8. During the delivery phase of a baseball pitch, what joint actions occur at the shoulder and elbow joints of the throwing arm?

Internal rotation, adduction, and extension at the shoulder joint; extension at the elbow joint

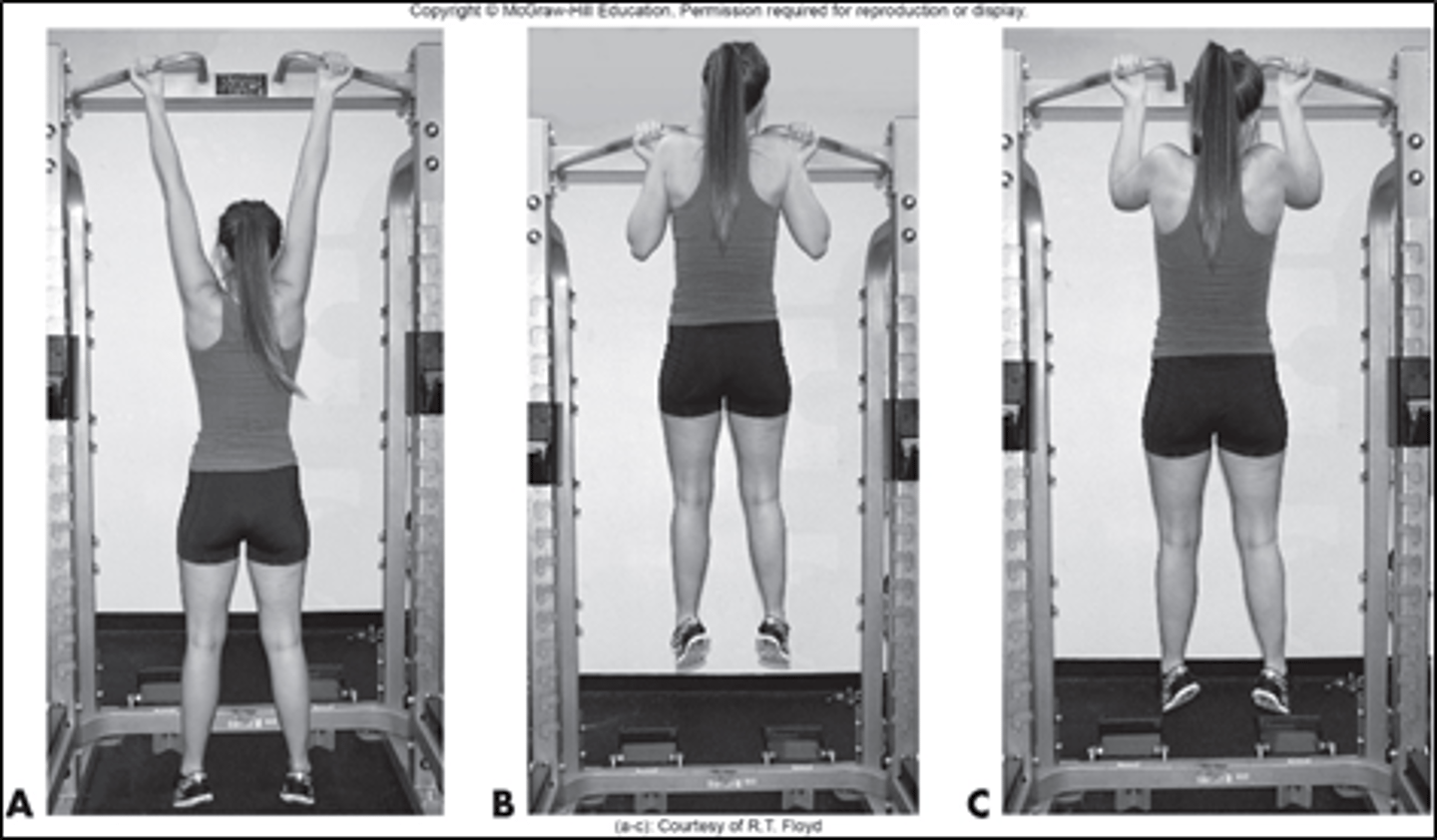
9. What joint action occurs at the shoulder joint and what are the plane and axis of motion during the pulling-up phase of a wide-grip pull-up?

Adduction in the frontal plane around the AP axis

How do the actions at the shoulder joint differ between a wide-grip pull-up and a narrow grip pull-up?

In a narrow-grip pull-up, extension and flexion occur at the shoulder joint in the sagittal plane around a transverse axis. In a wide-grip pull-up, adduction and abduction occur at the shoulder joint in the frontal plane around the AP axis