Precalc MATH 125 - DP

exam 1

Use transformations of the graph of y=x^4 or y=x^5 to graph the function:

• f(x) = 1/2(x-3)^4 + 3

Use transformations of the graph of y=x^4 or y=x^5 to graph the function:

• f(x) = (x+3)^5 + 4

Form a polynomial whose zeros and degree are given.

• Zeroes: -3, -2, 2

• degree: 3

f(x) = x³-4x+3x²-12 for a=1

Form a polynomial whose zeros and degree are given.

• Zeroes: 2, multiplicity 2; -2 multiplicity 2

• Degree: 4

F(x) = x^4 -8x²+16

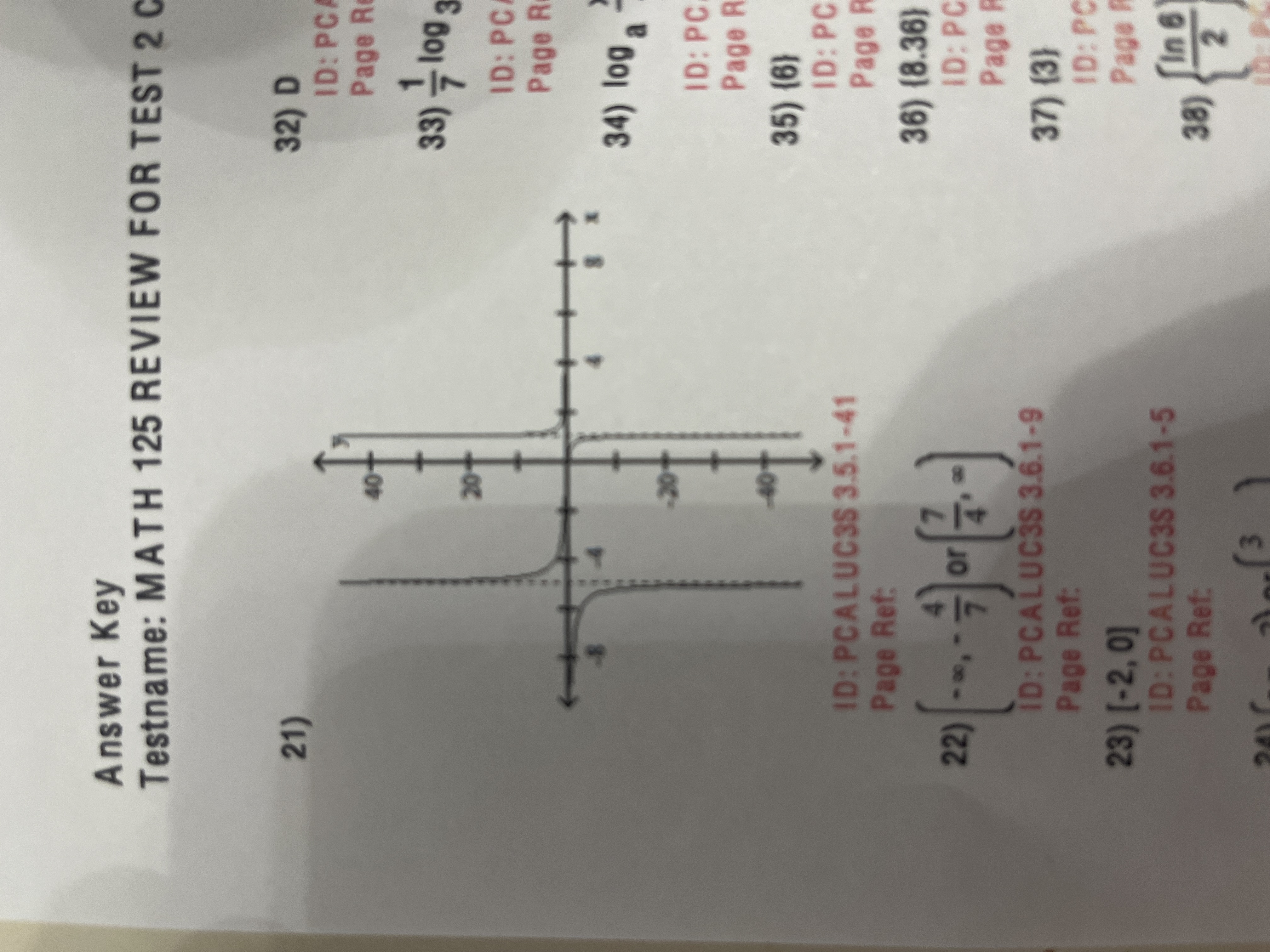
For the polynomial, list each real zero and its multiplicity. Determine whether the graph crosses or touches the x-axis at each x-intercept

• f(x) = 5(x-7)(x-5)²

7, multiplicity 1, crosses x-axis 

5, multiplicity 2, touches x-axis

Find the x - and y - intercepts of f.

• f(x) = (x+1)(x-9)(x-1)²

X-intercepts: -1, 1, 9

Y-intercepts: -9

Analyze the graph of the given function f as follows:

a) determine the end behavior: find the power function that the graph of f resembles for large values of |x|

b) find the x- and y- intercepts of the graph

c) determine whether the graph crosses or touches the x-axis at each x-intercept

d) graph f using a graphing utility 

e) use the graph to determine the local maxima and local minima, if any exist. Round turning points to two decimal places. 

f) use the information obtained in (a)-(e) to draw a complete graph of f by hand. Label all intercepts and turning points. 

g) find the domain of f. Use the graph to find the range of f. 

h) use the graph to determine where f is increasing and where f is decreasing 

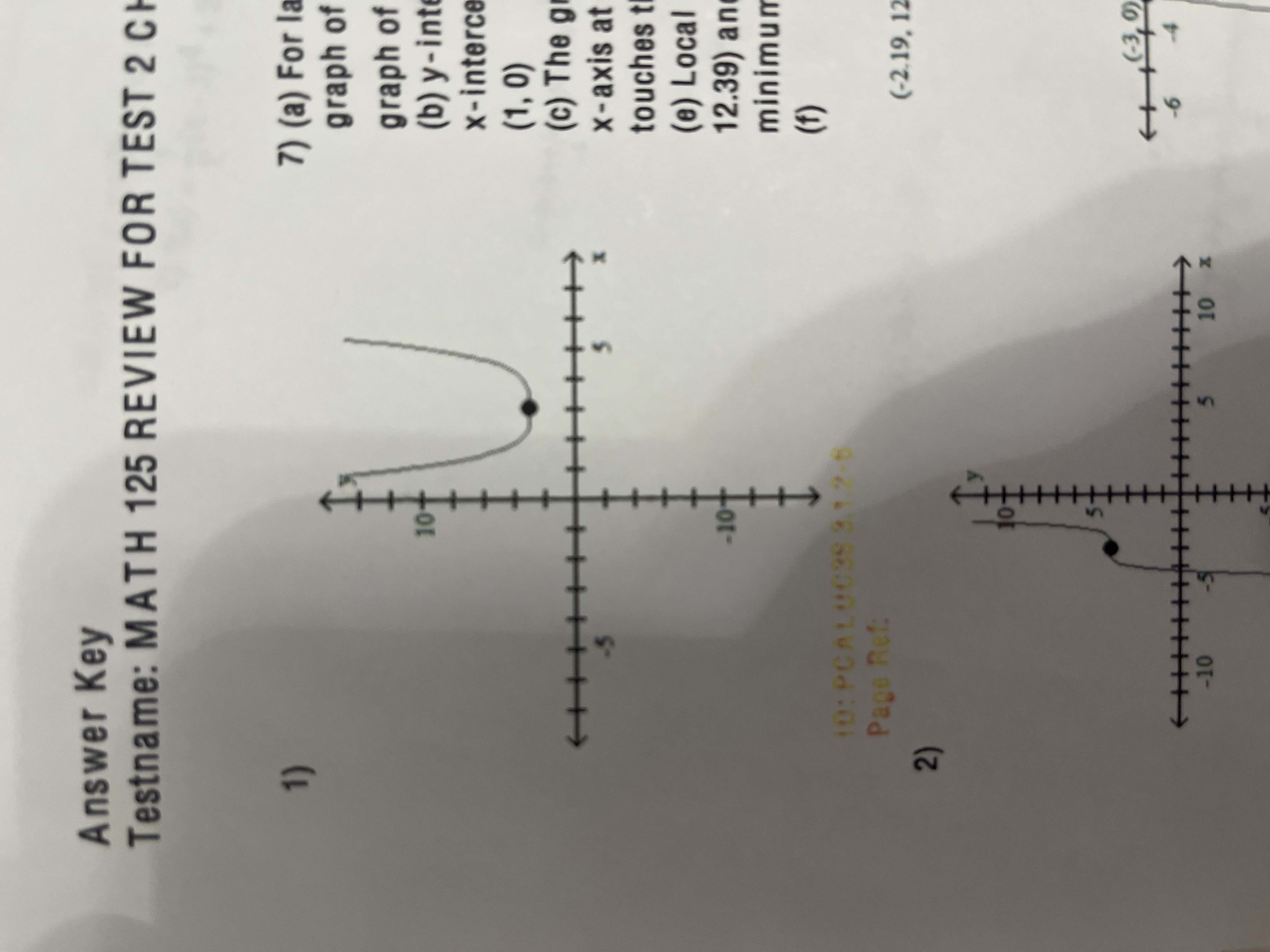
• f(x) = x²(x-1)(x+3)

(a) for large values of |x|, the graph of f(x) will resemble the graph of y=-x^4 

b) y-intercept: (0,0) ; x-intercepts: (-3,0),(0,0), and (1,0)

c) the graph of f crosses the x-axis at (1,0) and (-3,0) and touches the x-axis at (0,0)

e) local maxima at (-2.19,12.39) and (0.69,0.55) ; local minimum at (0,0)

f) GRAPH PICTURED BELOW

g) domain of f: all real numbers; range of f: (-infinity, 12.39]

h) f is increasing on (-infinity, -2.19) and (0,0.69) ; f is decreasing on (-2.19,0) and (0.69, infinity) 

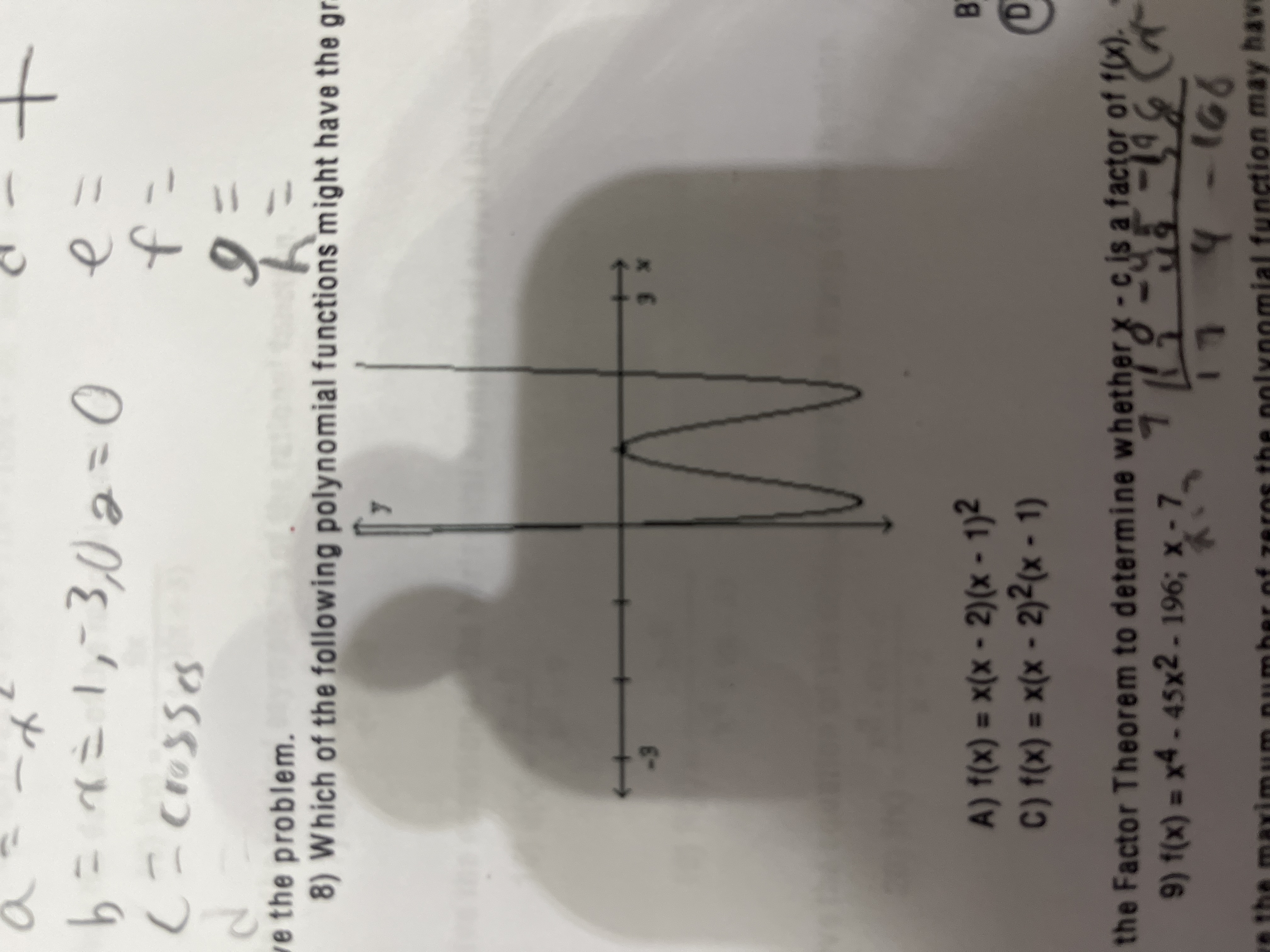
Solve the problem.

• which of the following polynomial functions might have the graph shown in the illustration below?

Answer choices:

A. f(x) = x(x-2)(x-1)²

B. f(x) = x²(x-2)(x-1)

C. f(x) = x(x-2)²(x-1)

D. f(x) = x²(x-2)²(x-1)²

A

Use the factor theorem to determine whether x - c is a factor of f(x)

• f(x) = x^4 -45x²-196 ; x-7

Yes

Hint: plug in for x. If zero, it IS a factor!!

Give the maximum number of zeroes the polynomial function may have. Use descarte’s rule of signs to determine how many positive and how many negative zeroes it may have. 

• f(x) = 4x^5 - 2x² + x+ 8

5; 2 or 0 positive zeroes; 1 negative zero

Lost the potential rational zeros of the polynomial function. Do not find the zeroes.

• f(x) = 6x^4 + 3x³-2x²+2

±1/6, ±1/3, ±1/2, ± 2/3, ± 1, ± 2

1. Identify leading coefficient (6) then identify constant (2)

2. Find factors of constant (p)

3. Find factors of coefficient (q)

4. Fractions (±) p/q

Use Descartes rule of signs and the rational zeroes theorem to find all the real zeroes of the polynomial function the zeroes to factor f over the real numbers. 

• f(x) = 2x^4-5x³+11x²-20x+12

1, 3/2; f(x) = (x-1)(2x-3)(x²+4)

Sign change with negative exponent; no sign change with positive exponent

1. Sign changes, however many = positive zeroes

2. Change to f(-x). Apply above rule

3. Sign changes, however many = negative zeroes

Solve the equation in the real numbers system

• 2x³-x²-14x+7=0

*hint group terms

{1/2, square root 7, - square root 7}

Form a polynomial f(x) with real coefficients having the given degree and zeroes. 

• degree: 3, zeroes: -2 and 3+i

*hint complex-conjugate rule

*hint factor each zero

f(x) = x³-4x²-2x+20

Use the given zero to find the remaining zeroes of the function.

• f(x) = 2x^4-19x³+71x²-109x +39; zeroes: 3+2i

3-2i, 3, 1/2

Find the domain of the rational function.

• h(x) = 9x/(x+5)(x+3)

{x|x does not equal -5, x does not equal -3}

Find the vertical asymptotes of the rational function.

• h(x) = x+9 / x²-49

X=-7, X=7

Give the equation if the horizontal asymptotes, if any, of the function

• g(x) = x+9 / x²-9

Y=0

Give the equation if the horizontal asymptotes, if any, of the function

• r(x) = -3x² / x²-8x-33

Y=-3

Give the equation of the oblique asymptote, if any, of the function

• f(x) = x² -6x+6 / x+2

Y=x-8

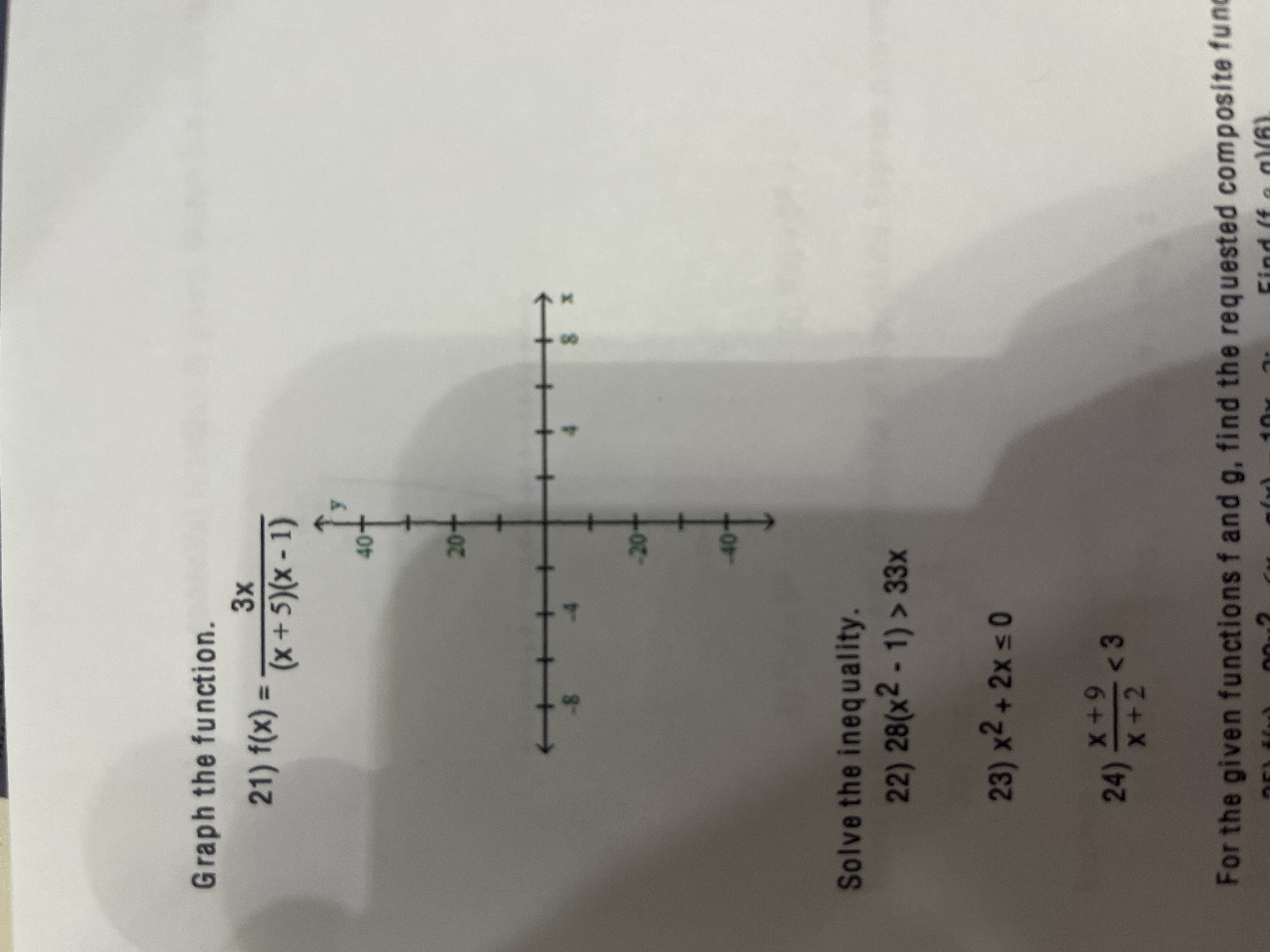
Graph the function

• f(x) = 3x / (x+5)(x-1)

Solve the inequality

• 28(x²-1)>33x

(-infinity, -7/4) or (7/4, infinity)

Solve the inequality

• x²+2x < or = 0

[-2,0]

Solve the inequality

• X+9 / X+2 < 3

(-infinity, -2) or (3/2, infinity)

For the given functions f and g, find the requested composite function value

• f(x) =20x²-6x, g(x)=19x-2

Find (f open circle g)(6)

250,208

For the given functions f and g, find the requested composite function value

• f(x)=6x+9, g(x) = 2x-1; find (f open circle g)(x)

12x + 3

Decide whether or not the functions are inverses of each other

• f(x) = 4x-9, g(x) = x+4 / 9

No

The function f is one-to-one. Find its inverse

• f(x) = x² +2, x > or = 0

F^-1(x) = square root x-2, x > or = 2

Solve the equation

2^x²-3 = 64

(2 and then rest is exponent)

{3,-3}

Solve the equation

• logg (x²-8x)=1

(Log and then g is small g)

{9,-1}

Solve the equation

• e^x+2 = 8

(e and then the rest is exponent)

{ln 8-2}

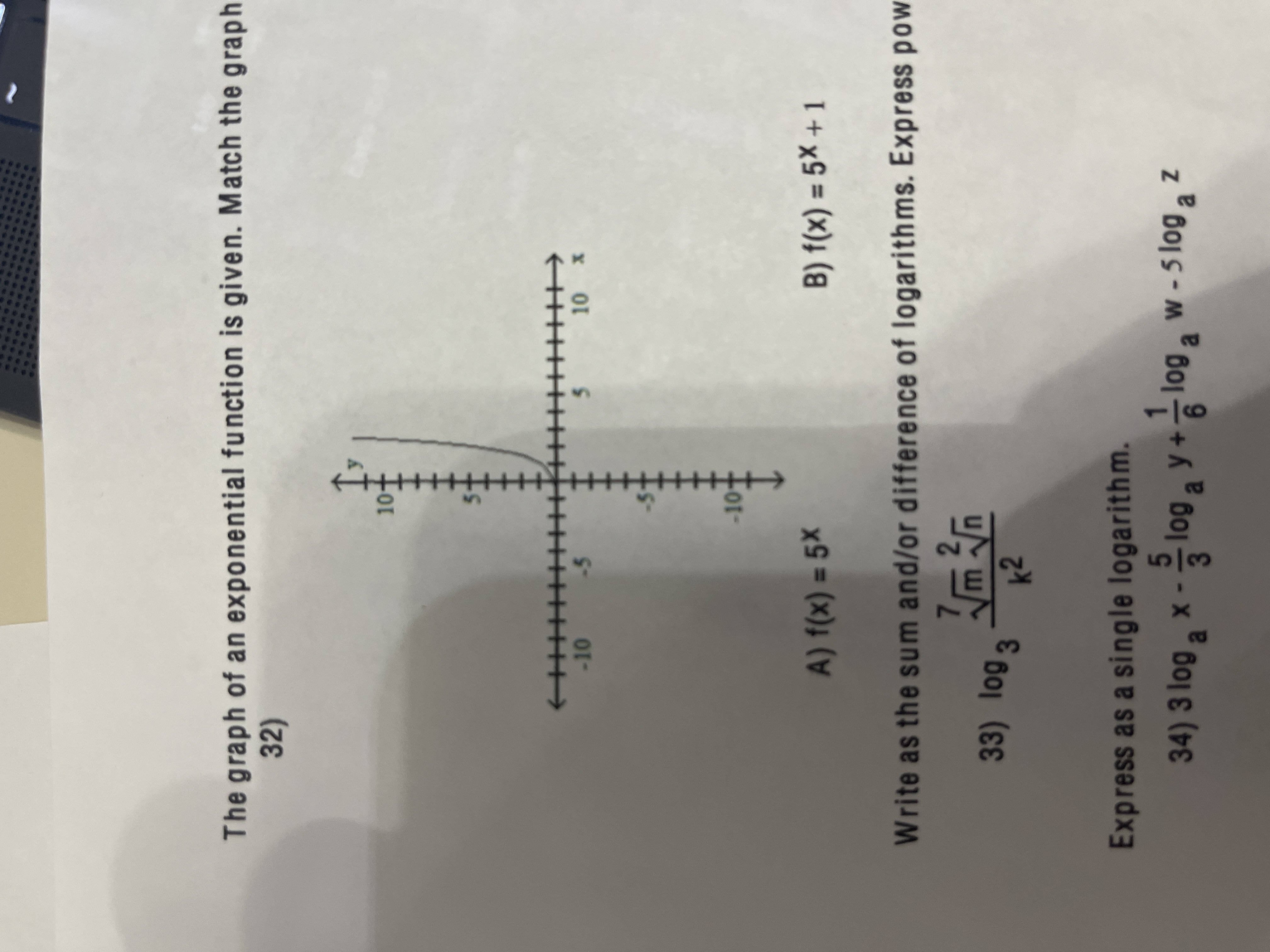
The graph if an exponential function is given. Match the graph to one of the following functions.

A) f(x)=5^x

B) f(x)=5^x + 1

C) f(x)= 5^x -1

D) f(x)= 5^x-1 (all exponent)

D

Write as the sum and/or difference of logarithms. Express powers as factors

• log3 7square root m 2square root n / k²

1/7log3 m+1/2 log3 n-2 log3 k

Express as a single logarithm

• 3 loga x - 5/3 loga y + 1/6 loga w - 5 loga z

Loga x³ w^1/6 / y^5/3 z^5

Solve the equation

• log2 (3x-2) - log2 (x-5) = 4

{6}

Solve the equation

• loga(x-7) - loga(x-2) = loga(x-4) - loga(x+12)

{8,36}

Solve the equation

• 2^(5-3x) =1/16

{3}

Solve the exponential equation. Express the solution set in terms of natural logarithms

• e^2x = 6

{ln 6 / 2}

Solve the exponential equation. Express the solution set in terms of natural logarithms

e^x - e^-x / 2 = 1

{ln (-1 + square root 2)}

Solve the problem

a fossilized lead contains 26% of its normal amount of carbon 14. How old is the fossil (to the nearest year)? Use 5600 years as the half-life of carbon 14

10,863