BCM. Energy and entropy

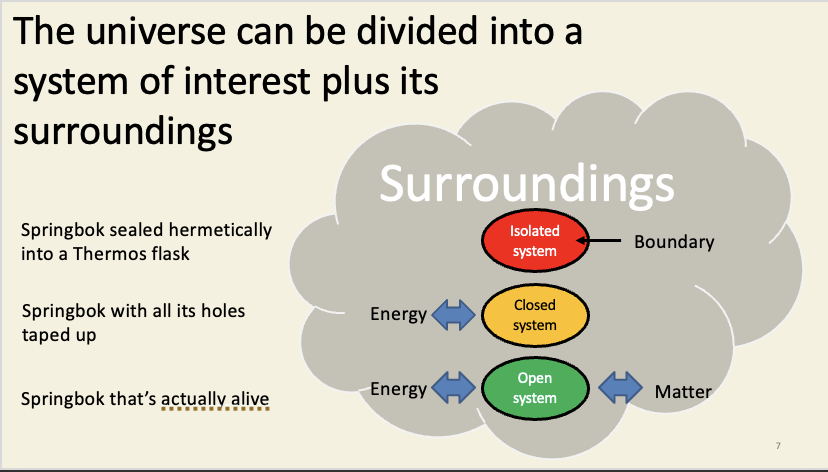
Systems

• you define what the system is

System kinds:

• isolated system - exchanges neither matter nor energy with the surroundings (easier to model)

• closed system - energy is exchanged with its surroundings

• open system - can exchange matter and energy with its surroundings (mathematically difficult to analyse)

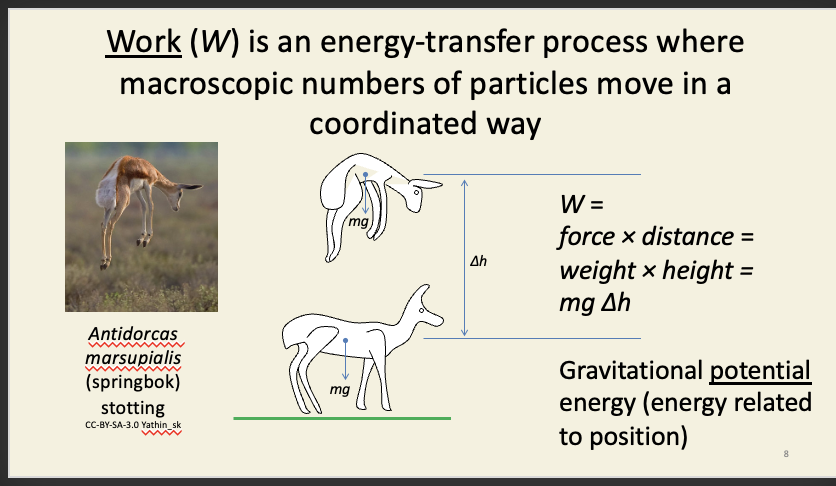
Work (W)

• all particles in the ‘system’ move upwards when the springbok jumps up

• can be used to calculated how much energy is needed to do this work

• Work is usually written as W.

• g here is the acceleration of gravity (9.81 m s⁻²), which is a measure of the strength of the Earth’s gravitational field at sea level. g itself varies with altitude and latitude, but not substantially enough to worry about here.

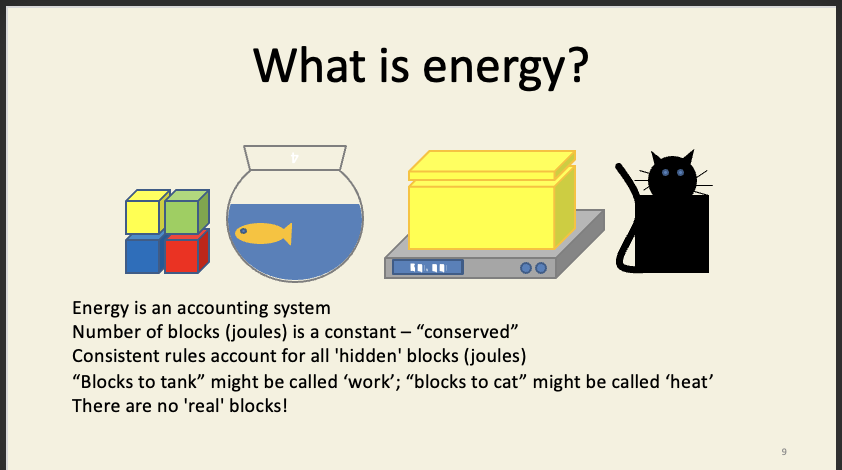
Energy

• energy is like the building blocks - e.g. can be transferred but neither created or destroyed - energy never exists in a ‘pure’ unadulterated form, it always exists as the mathematical accountancy of volume displacement, mass increase, and suspicious lumpiness

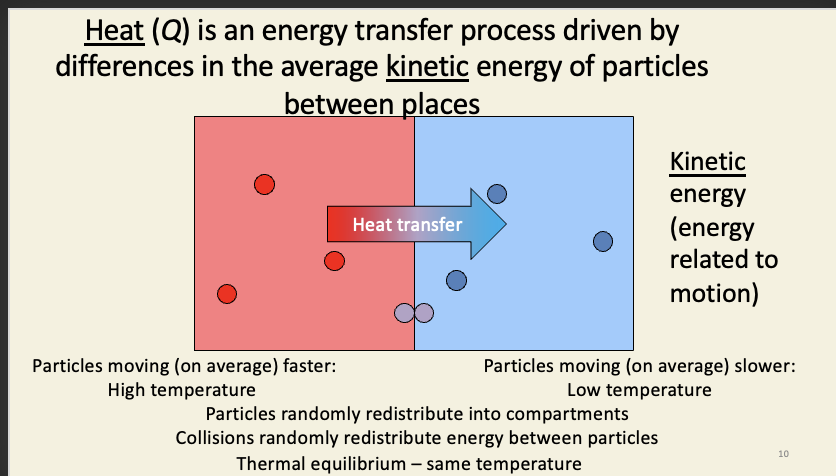
Heat (Q) 

• heat is the energy transfer process (not same as temperature) 

• particles are constantly in motion (apart from absolute freezing) 

• avg. KE of particles in the hotter compartment is higher than the colder compartment 

• collisions between particles = transfers energy from the fast moving particles to slow moving particles (results in mixture of fast, medium, and slow particles) 

First law of thermodynamics

• change in energy of the system = an equal and opposite change in the energy of the surroundings

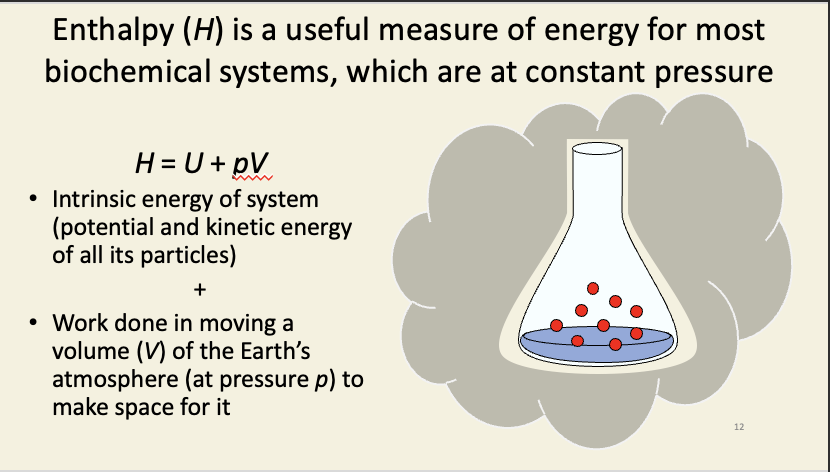
Enthalpy (H)

• intrinsic energy of the system + the work done on the earths atmosphere to make it exist

• intrinsic energy - energy needed to stick particles into the system

• U = W + Q, i.e. all the work done to put the particles into the system against gravitational/electrical/etc. fields in the surroundings and to therefore give them some particular potential energy; plus the heat energy required to warm them from absolute zero to some temperature, and to therefore give them some particular kinetic energy.

• The useful thing about enthalpy is that it factors-in any work done against (or by) the atmosphere. Most of the work that living things do is chemical, not mechanical, so this is a reasonable approach.

• The useful thing about enthalpy is that it factors-in any work done against (or by) the atmosphere. Most of the work that living things do is chemical, not mechanical, so this is a reasonable approach.

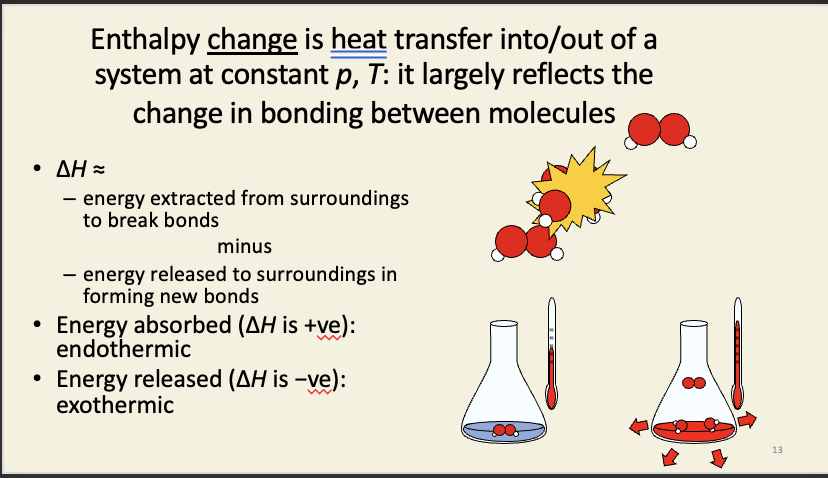
Enthalpy change 

• Most reactions in aqueous systems (e.g. hydrolysis of ATP in a cell) have no effect on the volume of the system = none of the intrinsic energy change is consumed in e.g. pushing the atmosphere out of the way during expansion.

• → the enthalpy change is more-or-less the same value as the intrinsic energy change

• the only other thing (besides volume) that can change during a simple chemical reaction is the arrangement of bonds between atoms.

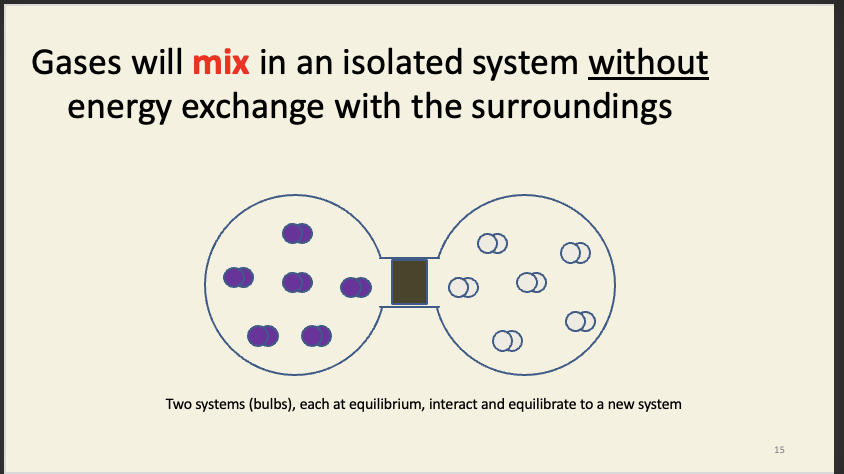
Entropy intro

• entropy - measure of disorder

Increasing entropy - more disorder

• adding energy into the system = ice melts into water but temperature change does not occur (this is because highly ordered ice particles are being turned into a much more disordered state - driven by entropy change)

Calculating entropy

• T = in kelvin 

• Q = Joules (J)

Second law of thermodynamics

• all processes increase the entropy of the universe

• when two equilibrium systems interact, they will equilibrate to a new system with the same or higher entropy than the original two systems

• energy is dispersed by all spontaneous processes

• you cannot convert temperature differences to work with 100% efficiency

Boltzmann

Microstate specifications

As long as the average molecular velocity remains the same, the temperature will be the same. As long as the total number of each kind of molecule remains the same, the overall composition will remain the same. As long as the average kinetic energy in each direction remains the same, the pressure will be unchanged. And so on. There are countless permutations of the particles that are indistinguishable at a macroscopic level.

If S = k_B ln Ω then Ω = e^S/k . For even a small entropy like 1 J.K⁻¹, Ω = e^{1/1.38*10^-23}=  e^{1.38*10^23}, that is e raised to the power of 13 800 000 000 000 000 000 000, which is inconceivably large!

Compatibility of microstates and macrostates

Equilibrating system 

• Nonequilibrium systems tend to evolve over time to equilibrium systems because systems take a random walk through “microstate space”, and this is overwhelmingly likely to wander into the ‘boring’ regions of this vast space than it is to wander into the exciting regions where e.g. all the alanine is in the L form, or all the iodine is in the left bulb, or all the fast-moving particles are in the same slab of metal.

• It’s the same process as coin flipping: each flip is equally likely to give a head as a tail, but getting 6.022 × 102³ heads in a row is ‘very’ unlikely.

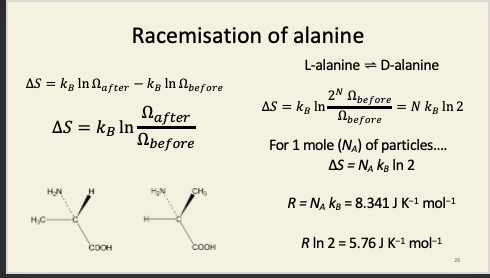
Racemisation of alanine

• In a system composed of pure L-isomer, before the racemase enzyme is added, there are a ludicrously large number of compatible microstates, so how on earth do we go about calculating Ω _before? We don't. What we do note is that – however many compatible microstates there are before we add the enzyme, there will be 2^N times as many possible compatible microstates in the presence of the enzyme, where N is the number of particles in the system. Why? Each and every particle in the system can now be in one of two states (D or L), so, for every particle present, we double the number of possible microstates of the system.

  This is actually the two-bulb experiment in disguise. Imagine you had two bulbs, each filled with either D or L alanine, and separated by a biological membrane. If there were D- and L-specific pores in that membrane, then each amino acid would flow down its own concentration gradient into the other bulb. If those pores were ATP synthase enzymes, this could be coupled to the phosphorylation of ADP to ATP. There is energy associated with “all D” and “all L” compared to “equimolar mixture of D and L”: the directional flow can be coupled to the doing of useful chemical work in just the same way that proton flow can be coupled to ATP production in mitochondria and plastids. However, if the pores were just holes, each amino acid would simply flow down its gradient, until eventually both were at the same concentration in both bulbs. Once we reach an equimolar mixture of D and L isomers, no useful work can be done, because the energy  of the two gradients has now been dissipated. Note that adding racemase to both bulbs at the same time would have the same eventual effect as removing the barrier between the two bulbs: you’d end up with racemic mixtures in both compartments. Entropy is a state function: its final value doesn’t actually depend on how you get there. The entropy change in allowing two (idealised) gases to mix (like the oxygen and iodine vapour we saw earlier) is the same as the entropy change of racemisation: in both cases, every molecule has twice as many available states at equilibrium as it does before (D vs. L for the amino acids; left bulb or right bulb for the gases), so the entropy increases by R ln(2) in both cases

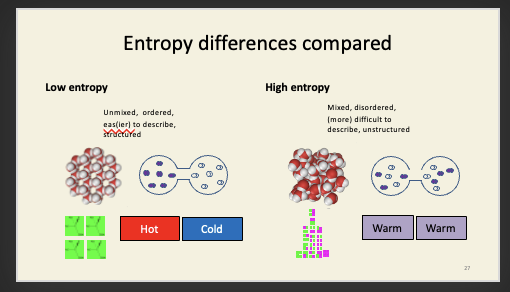
Entropy differences compared

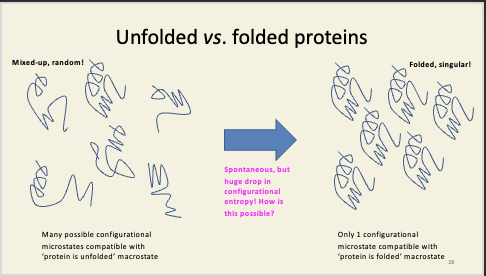
Unfolded vs. folded proteins

• unfolded = many microstates can be compatible

• folded = only one possible configuration of microstate is compatible with this enzyme