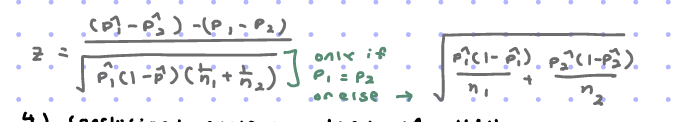Review- Chapter 8 Statistics

Statistical inference

• drawing a conclusion about a population parameter based on a sample statistic

Confidence Interval

• used to estimate the value of a parameter with a range of plausible values

• estimate population proportion(p) with a z test

• " I am % confident that the true proportional of ALL is within the interval__to__)

• Width of CI=1/√n

• CI increase →width increase →z* increase

• CI decrease →width decrease →ME and SE decrease

• MORE narrow graph

  • decrease CI or Increase n

• Higher CI

  • accept a wider interval OR increase n

*MUST compare to population, not only the sample

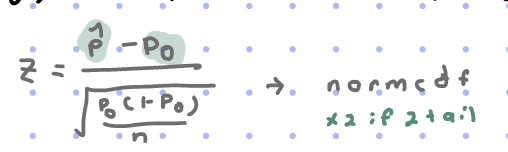
1 Proportion Z test

Confidence Level

• “if you took ____samples and constructed the resulting confidence interval, the true proportion of ALL___ will be in __%(as a number) of these intervals”

  increase

Significance test

• Assess the plausibility of a particular claim about a parameter

• TEST claim about the population(p) with a z-interval

CONDITIONS

1. Random sample(SRS)

2. n₁ p₁ >=10, n_1(1- p₁ )>=10

3. The sample size is <= 10% of the population size

• condition of independence & not population >10n =okay!

• the increase in variation due to the dependence almost offsets the decrease due to a relatively large sample

STEPS

Title

1. Conditions

2. Hypothesis, label

3. Test statistic→pvalue→diagram(if need)

4. Conclusion in context, doubts of validity

   1. Compare p-value with α, level of significance

   2. compare test stat to z*

• “Since p value _α, there is/is not statistically significant evidence to reject the null hypothesis, that is there is/is not statistically significant evidence…’

Pooled estimate

p̂ =total success in BOTH sample size/total sample size

means and standard error of sampling distribution formula

P value

• probability of obtaining a sample statistics as EXTREME or MORE EXTREME than one obtained by the null hypotheses( H_o ) is assumed to be true

• small(<0.05,0.1)→ sufficient evidence to reject H_o

z*

• Critical z

• Ways to increase z*

  1. farther p̂ from p

  2. sample size decrease

  3. p_o farther from 0.5

Margin of error

• exactly ½ the width of CI

• determined by…

• small MOE→ large n

1. how MUCH statistic typically varies from parameter σ_p̂

2. how confident do we want our answer to be z*

MATH

z*√((p̂(1-p̂))/n

use 0.5 for p̂ if not given

Hypothesis

H_o = null hypothesis, must use an = sign

H_a= alternate hypothesis, can use <, >, <=,>=, ≠

• defines the parameter of interest → refers to the population

p̂

sample proportion

p_o

assumed proportion in the null hypotheses(H_o ), the given in text

2 tail

≠

2p(z____)

1 tail

• either < or >

• in context, could be testing for strength, effectiveness…

Errors

are inversely related

Type I error (α)

• rejecting the null hypotheses(H_o ) when it is true

• increase if α increase

Type II error(β)

• failing to reject null hypotheses(H_o )when its false

• MORE likely for small n

  *the only way to have power

Power

(1-β)

• probability that type II error does not occur → correctly rejecting null hypotheses(H_o )when its false

• influenced by α

Power Increase by…

1. n Increase

2. α Increase

3. SE decrease

4. True parameter further from null

Difference of 2 Proportions

CONDITIONS

1. 2 samples are taken randomly or randomly assigned

2. n₁p̂_{1 ,} n₁(1-p̂₁)_, n₂p̂_2, n₂(1-p̂₂) >=5

3. The sample size is <= 10% of the population size

Confidence Interval of Difference of 2 Proportions

Captures 0

• yes → __% confident that there is no difference between p1 and p2

  →means that 1 value is positive, 1 value is negative

• no → __% confident that there is a difference between p1 and p2

  →not plausible for there to be no difference

• n can sometimes be split in half

• “the true difference in proportion between___and___is”

• 2 groups having the SAME “proportion”→ risk ratio =1, so for a positive/greater proportion than the other CI range is the decimal +1.

Test statistic of Difference of 2 Proportions

STEPS
name 2 proportion z test

result → C up, C Low

1. Conditions

2. Hypotheses

3. Test statistic → p value → diagram(if need)

4. Conclusion in context, doubts of validity

   1. compare p value and α