quarks to cosmos: final exam

What is the difference between white dwarfs, neutron stars & pulsars, and black holes?

• White dwarfs are remnants of stars that have exhausted their nuclear fuel, around the same size as Earth (7000km) but 200k times denser

• neutron stars are incredibly dense cores left after supernova explosions, around 10k in size.

  • pulsars are rotating neutron stars that emit beams of radiation

• black holes are regions in space where gravity is so strong that nothing can escape from them.
  

  key differences lie in their formation and characteristics: white dwarfs are less dense and smaller than neutron stars, which are more massive and formed from supernovae; pulsars are a specific type of neutron star that emits radiation due to rotation; black holes are the remnants of massive stars with gravitational pull so strong that not even light can escape.

What different types of stars become these objects, relative sizes, how do we detect them, what forces hold them up (push against gravity)

Different types of stars become these objects based on their mass and life cycle stages. White dwarfs form from low to medium-mass stars, neutron stars from massive stars that undergo supernova explosions, and black holes from the remnants of very massive stars.

Detection methods vary:

• white dwarfs are observed through their thermal emissions through telescopes, although very faint and small

• neutron stars through gravitational influence on their surroundings, strong magnetic fields can exist around neutron stars that also cause light to be created, gravitational waves

• pulsars via their radio pulses/radio waves through a radio telescope

• black holes indirectly through their effects on nearby matter and light, because they don’t directly emit or reflect light.

What is escape velocity?

Escape velocity is the minimum speed an object must reach to break free from a celestial body's gravitational pull without any additional propulsion. It depends on the mass and radius of the body. It is the speed needed to overcome gravitational attraction.

How do we calculate escape velocity?

Escape velocity is calculated using the formula: (image)

• G is the gravitational constant

• M is the mass of the celestial body

• r is its radius.

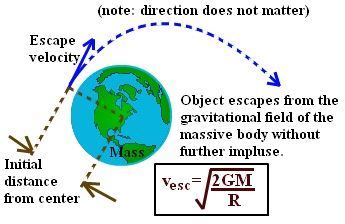
How is escape velocity key to determining what a black hole is?

Escape velocity is crucial in determining what a black hole is because it defines the speed needed to escape a black hole's gravitational pull. If an object's escape velocity exceeds the speed of light, it cannot escape the black hole's influence, leading to the conclusion that nothing, not even light, can escape from it.

What is an event horizon?

The boundary around a black hole beyond which nothing can escape, including light. Escape velocity = speed of light. It marks the point of no return for objects approaching the black hole. If mass ( M ) increases or the radius ( r ) decreases, gravity gets bigger, more KE can escape.

vesc (escape sound) = c (speed of light).

The speed of light is constant in all reference frames. How does this apply to the idea that different observers will measure different distances and times for events?

The speed of light is a constant in all references frames, regardless of their relative velocity. Thus, time and space are relative to the observer.

The constancy of the speed of light means that all observers, regardless of their motion, measure the same speed for light (c). This principle underpins special relativity (there is no special place in the universe) and leads to key effects like time dilation and length contraction.

• Time dilation: A moving clock ticks more slowly as observed from a stationary frame. This ensures that the time interval measured by different observers adapts to keep the speed of light constant.

• Length contraction: Objects moving relative to an observer appear shorter in the direction of motion. This change in measured length, combined with time dilation, ensures consistency in light-speed measurements.

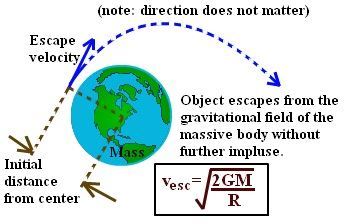
How do the observers in the train and on the ground observe different things with the example in class of the light going up and down in the moving boxcar?

Train Observer:

• Sees the light beam travel straight up and down vertically.

• The motion is purely vertical because they are stationary relative to the boxcar.

Ground Observer:

• Sees the light beam travel diagonally in a V-shaped path.

• This is because the boxcar moves horizontally while the light travels vertically.

Key Differences:

• For the train observer, the light travels a shorter vertical path.

• For the ground observer, the light travels a longer diagonal path due to the boxcar's horizontal motion.

• Different observers measure different times between events. They also measure different distances between events.

• Time and space are relative to the observer— relative to your frame of reference
  

Einstein determined that space and time were part of the same thing—that all observers must agree on the “spacetime” of events.

What is the principle of equivalence?

The principle of equivalence, a cornerstone of Einstein's general theory of relativity, states that the effects of gravity and acceleration are indistinguishable in small, localized regions of spacetime.

This essentially means that gravity and acceleration are equivalent; there is no way to distinguish between being in a uniformly accelerating reference frame and being in a gravitational field.

• A reference frame in free-fall cannot be distinguished from an inertial reference frame. (in order to be in a free fall, there must be gravity)

• “inertial reference frame”- uniform motion: no forces

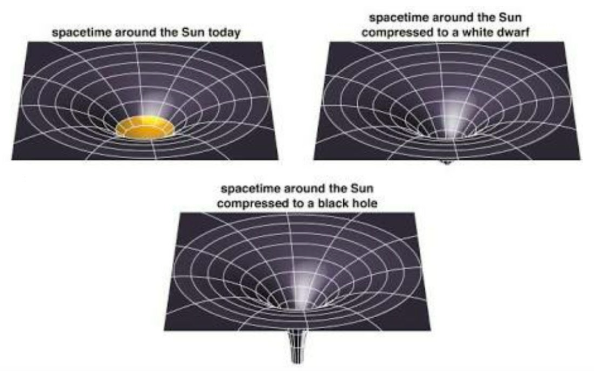
How does the principle of equivalence imply that gravity can bend the path of light?

(use the analogy of the two elevators— one in free fall and one off in space without any forces acting on it, which is an “inertial” reference frame)

• Being in a freely falling elevator is equivalent to being in an inertial reference frame (no forces acting).

• Being in an elevator at rest in a gravitational field is equivalent to being in one accelerating upward in space without gravity.

1. Elevator in Deep Space (No Gravity):
   In deep space, a light beam entering an elevator travels in a straight line, as there is no gravity or acceleration.

2. Freely Falling Elevator:
   In free fall, the elevator and everything inside accelerate downward equally. To someone inside, the light still seems to travel straight, but to an outside observer, the elevator's downward motion causes the light to appear curved.

3. Elevator at Rest in Gravity:
   On Earth, the elevator is stationary in a gravitational field. A light beam entering appears to bend downward, just as it would in an accelerating elevator in space, illustrating how gravity affects the path of light.

Light traveling in a "straight line" in an inertial frame will appear curved in a frame affected by gravity or acceleration.

This is why massive objects, like stars or black holes, bend the path of light passing near them (gravitational lensing).

Light will always find the shortest path between two points— but the shortest path in 4-dimensional spacetime is not always the shortest path in our 3-dimensional space.

How does the presence of a gravitational field impact time, and how do clocks move slower in a gravitational field?

Einstein's theory of general relativity predicts that where gravity is stronger, time passes more slowly. That's called time dilation. Gravity is stronger closer to the center of the Earth. So, according to Einstein, time should pass more slowly closer to the ground.

Time slows down in stronger gravitational fields because mass curves spacetime. Clocks near massive objects tick slower compared to those farther away. For distant observers, the clock in strong gravity appears slower due to time stretching. This effect is key to GPS satellite adjustments and is a direct prediction of general relativity.

What is the structure of the Milky Way Galaxy?

• Galactic Disk:

  • Contains stars, gas, dust, and spiral arms.

  • Most of the galaxy's stars, including the Sun, are located here.

  • Active regions of star formation are found in the spiral arms.

• Galactic Bulge:

  • A dense, spherical region at the center of the galaxy.

  • Composed of older stars, little gas or dust, and a supermassive black hole.

• Galactic Halo:

  • A roughly spherical region surrounding the disk and bulge.

  • Contains old stars and globular clusters.

  • Almost no gas or dust, and is dominated by dark matter.

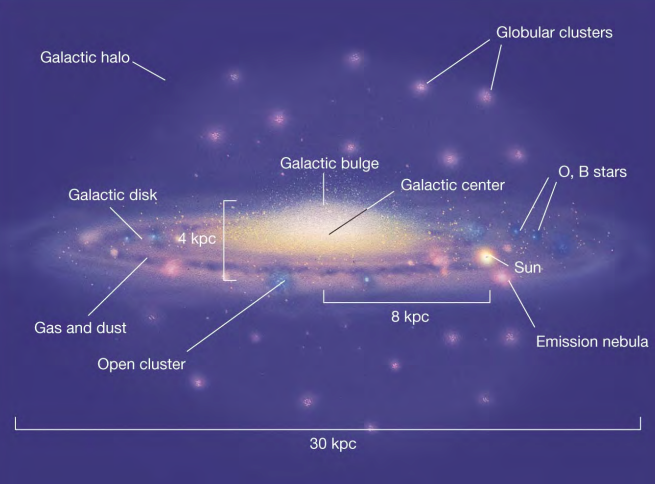
In the Milky Way Galaxy: Where are the stars? Where is the gas? What’s in the halo?

• Stars:

  • Galactic Disk: Most stars, including the Sun, are found here, especially in the spiral arms where active star formation occurs.

  • Galactic Bulge: Older stars are concentrated in the dense central region of the galaxy.

• Gas:

  • Galactic Disk: The gas is primarily found in the interstellar medium of the disk, especially in the spiral arms, where it fuels star formation.

  • Galactic Bulge: Less gas here, but there is still some, especially near the central black hole.

• Halo:

  • Contains old stars and globular clusters (tight groupings of older stars).

  • Very little gas or dust.

  • Dominated by dark matter, which provides the gravitational pull to hold the galaxy together.

How do the stars and gas in the Milky Way Galaxy move?

Stars and gas in the Milky Way Galaxy primarily move in an orderly rotation, with most stars within the galactic disk orbiting the galactic center in nearly circular paths, all generally moving in the same direction, similar to a spinning record, while stars in the halo have more randomly oriented orbits. 

• Stars in the Disk:

  • Move in circular orbits with differential rotation (inner stars faster).

  • Bob up and down relative to the disk.

• Gas in the Disk:

  • Rotates around the center, often in spiral arms, with turbulent motion.

• Stars in the Bulge:

  • Move in random, elliptical orbits.

• Stars and Gas in the Halo:

  • Move in elliptical orbits with high velocities and random motion.

How do we use the rotation speed of the disk of the Milky Way to estimate its total mass? What was the conclusion from these calculations?

• Rotation Speed and Mass:
  The orbital speed of stars (v) gives the total enclosed mass using M = v²r / G

• Flat Rotation Curve:
  Observations show that the rotation speed remains constant at large distances, rather than decreasing as expected if mass were only in visible stars and gas.

• Conclusion:
  The flat curve reveals the Milky Way is surrounded by a dark matter halo, making up most of its mass

• Out at around 30 kpc from the center of the galaxy, the rotational speed is measured at ~200 km/s.

• Using our equation, we can calculate the amount of mass needed to sustain that rotational velocity.

• From looking at starlight, we can estimate the amount of mass in stars within the Milky Way galaxy.

• Comparing these two numbers, the stars account for less than half of the mass required to produce the MWs rotational motion.

• Thus, most of the mass in the MW indicates the presence some unseen “dark matter.”

What is the equation for circular motion and how do we use it?

The force of gravity between two masses, M1 (central object) and m2 (orbiting object)

Objects like planets, stars, or gas clouds move in circular orbits because of gravity. Gravity acts as the centripetal force that keeps these objects in orbit around a massive central object, like a star, black hole, or galaxy.

• Estimating Mass: Orbital speeds and distances reveal the mass of stars, galaxies, or black holes.

• Dark Matter Discovery: Stars in galaxies orbit faster than expected, showing the presence of invisible dark matter.

What is in the center of the Milky Way? How do we know its there?

A supermassive black hole is in the center of the milky way.

1. Star Orbits:

   • Stars near the center orbit very quickly around an invisible massive object.

   • By tracking these orbits, astronomers calculated the mass of Sgr A* to be about 4 million times the Sun’s mass.

2. X-Ray and Radio Waves:

   • Powerful emissions of X-rays and radio waves come from the region, consistent with material falling into a black hole.

What is the equation for Hubble’s Law? How did Hubble get the data to make the law?

The units of H are a bit odd: the best fit value of that slope is H = 72 km/s/Mpc

how?

• Measured Distances (r):

  • Used Cepheid variable stars, which have a known relationship between their brightness and pulsation period, as standard candles to calculate their true luminosity and determine the distance to galaxies.

• Measured Velocities (v):

  • Used redshift of light from galaxies to determine how fast they are moving away.

• Found Relationship:

  • Plotted v vs. rrr and discovered they are proportional, showing that galaxies farther away are moving faster, evidence of the expanding universe.

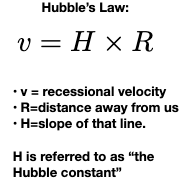
How do you calculate the Hubble constant?

v = H₀ × r

Where:

• v is the recessional velocity (km/s),

• r is the distance to the galaxy (in megaparsecs, Mpc),

• H₀ is the Hubble constant (in km/s/Mpc).

how to calculate?

• Measure the Recessional Velocity (v):

  • Using redshift from galaxy spectral lines to determine how fast the galaxy is moving away.

• Measure the Distance (r):

  • Use standard candles (like Cepheid variable stars or Type Ia supernovae) to calculate the galaxy's distance.

• Calculate the Hubble Constant (H₀​):

  • Rearrange equation to H₀ = v / r

How is recessional velocity of a galaxy calculated using by Doppler shifts?

by looking at the spectra..

The recessional velocity (v) of a galaxy can be calculated using the Doppler shift with this formula:

v / c = Δλ​ / λemit​

Where:

• v is the recessional velocity,

• c is the speed of light,

• Δλ is the change in wavelength (λobs−λemit)

• λemit is the emitted wavelength.

steps:

1. Measure the observed wavelength (λobs) and compare it to the emitted wavelength (λemit)

2. Calculate the change in wavelength (Δλ)

3. Use the formula to calculate the velocity: v = Δλ / λemit × c

This method reveals how fast the galaxy is moving away based on the shift in its light.

also can use z = v / c

• z is redshift

• v is recessional velocity of the galaxy

• c is speed of light

• The redshift z measures how much the light from a galaxy has shifted due to its motion away from us.

• To find the recessional velocity, rearrange the formula: v = z × c

This formula helps calculate how fast a galaxy is moving away based on its redshift.

How does Hubble’s Law combine with the Cosmological Principle to imply that the universe is expanding?

• Hubble’s Law: galaxies move away from us, and the farther they are, the faster they recede.

• Cosmological Principle: The universe is homogeneous and isotropic, meaning it looks the same everywhere and in every direction on large scales.

Together, these imply that the universe is expanding uniformly, with galaxies receding from each other, and the expansion happening the same everywhere.

How does the expansion of the universe create the Doppler shifts that we see in far away galaxy spectra?

space is expanding, and the light expands with it.

As the universe expands, the space between galaxies stretches, causing the light from distant galaxies to redshift (shift to longer wavelengths). This happens because the wavelengths of light are stretched as they travel through expanding space. The farther a galaxy is, the greater the redshift, reflecting the rate of expansion. This redshift is a cosmological Doppler shift, similar to the Doppler effect, but caused by the expansion of space itself.

If the emitter or observer have relative velocity (along the line of sight), the wavelengths observed are not the same as wavelengths emitted

All these spectra have the same set of lines, just shifted further and further to the right (redder longer wavelengths).

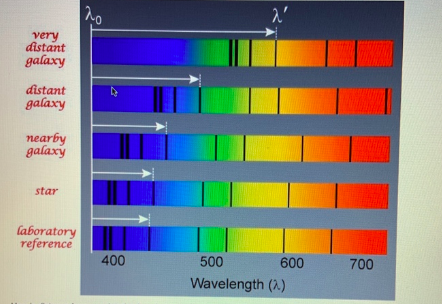
What does “redshift” mean in terms of the relative size of the universe?

Redshift refers to the stretching of light’s wavelength, which occurs when an object (like a galaxy) moves away from the observer. In the context of the universe, redshift indicates that the universe is expanding. Higher redshift = larger expansion.

Redshift is a sign of the universe’s expansion—more redshift means the universe has expanded more since the light was emitted, indicating a larger universe today.

to calculate:

• As space expands, it stretches out the light. Thus, if Δλ / λ = 1, then the universe today is twice the size as the universe was when the light was emitted.

• Redshift z is a measure of the relative size of the universe.

• R = 1 / 1 + z, where R is the relative size of the universe

What are the three different types of galaxies? How do their properties compare to each other Shape, motions, colors, different populations of stars?

1. Elliptical Galaxies:

   • Shape: Oval or ellipsoidal; no distinct structure. No disk, no halo, essentially a big bulge. No gas/dust.

   • Motion: Stars move in random, irregular orbits. Little to no rotation.

   • Colors: Generally reddish due to older stars (mainly low-mass stars).

   • Star Population: Primarily older stars, no spiral arms: no star formation.

   2. Spiral Galaxies (MW):

   • Shape: Flat, disk-like structure with spiral arms, a central bulge, and a halo.

   • Motion: Stars and gas mostly orbit in the disk, with some random motion in the bulge.

     • “differential rotation”—inner angular rotation is faster than outer angular rotation.

   • Colors: Blue in the spiral arms (due to young, hot stars) and yellow or red in the bulge (due to older stars).

   • Star Population: A mix of young stars (in the spiral arms: “density waves”) and older stars (in the bulge). Active star formation in the arms.

   3. Irregular Galaxies:

   • Shape: No defined shape, often asymmetric and chaotic. No clear disk.

   • Motion: Stars move in random directions; lack a coherent structure.

   • Colors: Varied, with blue areas indicating ongoing star formation.

   • Star Population: Both young and old stars; often active star formation.

What happens when galaxies merge with each other?

• Their shapes distort and can form elliptical or irregular galaxies.

• Gas clouds collide, triggering intense star formation (starburst).

• Supermassive black holes may merge, creating quasars or active galactic nuclei.

• Some stars may be ejected, and new stars may form.

• Over time, a larger galaxy is formed.

The merger “disrupts” the disk: the normally ordered rotational motion is converted into chaotic random motions. No more disk: ellipsoid.

The merger smashes together all the gas, which is rapidly converted into stars at elevated rate: No more gas. No more star formation. Red colors.

“Major mergers” are when the two galaxies are close in mass. These are the types of mergers that create elliptical galaxies.

“Minor mergers” are when the secondary galaxy is significantly smaller than the primary galaxy. The remnant of the merger is still a spiral galaxy, but is larger.

What are the three possible fates of the universe?

• Too Heavy (Closed Universe) – If the universe has enough mass, gravitational forces will eventually slow the expansion, reverse it, and cause a Big Crunch, where the universe collapses back on itself.

• Too Light (Open Universe) – If the universe has too little mass, it will expand forever, but at a decreasing rate. This leads to the Big Freeze, where the universe becomes increasingly cold and dark as stars burn out and matter spreads out.

• Just Right (Flat Universe) – If the universe's mass is just right, the expansion will slow down but never completely stop. The universe will expand forever at a steady rate, leading to the Big Freeze. This is the most likely scenario, given current observations.

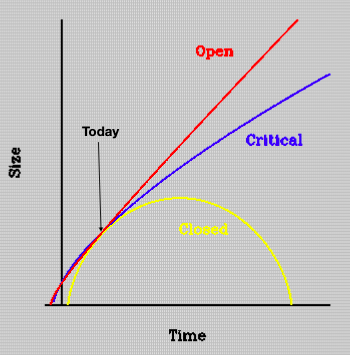
How do the three possible fates of our universe relate to the “critical” density?

The critical density is the specific density of the universe that determines its ultimate fate. It represents the exact amount of matter and energy needed for the universe to expand at a rate that would stop after an infinite amount of time but never collapse back in on itself.

1. Too Heavy (Closed Universe):

   • If the universe's density is greater than the critical density, gravitational forces will eventually slow the expansion and reverse it, causing the universe to collapse back in on itself in a Big Crunch.

2. Too Light (Open Universe):

   • If the universe's density is less than the critical density, it will continue to expand forever, but the expansion will slow down over time. Eventually, this leads to the Big Freeze as stars burn out and the universe becomes dark and cold.

3. Just Right (Flat Universe):

   • If the universe's density is exactly equal to the critical density, the expansion will continue forever, but at a slower rate, eventually leading to the Big Freeze without ever collapsing or slowing completely. until t = infinity

How do the three possible fates of our universe relate to the three possible “geometries” of the universe, as indicated by Einstein’s General Relativity? What do light rays do in the three geometries?

Closed Universe (Positive Curvature)

• Geometry: Spherical, like the surface of a ball.

• Fate: If the universe's density is greater than the critical density, it will eventually collapse in a Big Crunch.

• Light Rays: Light curves inward, and distant objects appear closer due to the curvature.

2. Open Universe (Negative Curvature)

• Geometry: Hyperbolic, like a saddle.

• Fate: If the universe's density is less than the critical density, it will expand forever, leading to a Big Freeze.

• Light Rays: Light rays diverge, and distant objects appear farther apart.

3. Flat Universe (Zero Curvature)

• Geometry: Flat, like Euclidean space.

• Fate: If the universe's density is exactly at the critical density, it will expand forever but slowly, leading to a Big Freeze.

• Light Rays: Light travels in straight lines.

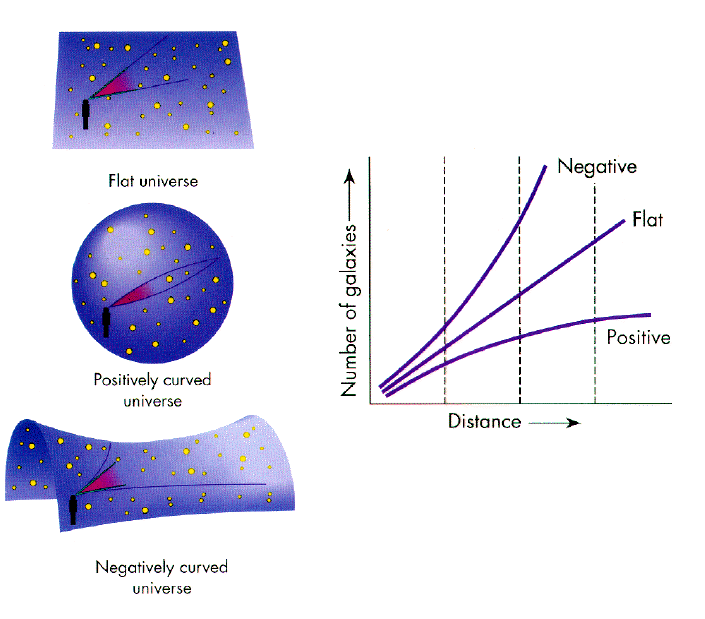
We think our universe is a low-density universe but has a flat geometry. What are the main observational pieces of evidence pointing to this result?

1. Ages of Globular Clusters: The oldest clusters suggest the universe is about 13.8 billion years old, which fits a flat universe model.

2. CMB Spot Sizes: Temperature fluctuations in the CMB match the predictions for a flat geometry.

3. Supernova Distances: Observations of distant supernovae show accelerating expansion, consistent with a low-density, flat universe.

These observations support the idea of a low-density, flat universe.

How does the Hubble constant relate to the age of the universe?

Age of the universe = 1 / H₀

• The Hubble time gives an estimate of the universe's age.

• Units: If H₀​ is in km/s/Mpc, the age will be in billions of years.

As the value of H₀​ increases, the estimated age of the universe decreases, and vice versa.

How does the matter density relate to the age of the universe?

The matter density of the universe affects its age:

• Higher matter density (Ω_m > 1): The universe would have collapsed sooner, so the age of the universe would be younger.

• Lower matter density (Ω_m < 1): The universe would have expanded more slowly, so the age of the universe would be older.

• More matter → younger age

• Less matter → older age

We observe that the expansion of the universe is currently speeding up. How does Einstein’s Cosmological Constant explain that data?

Einstein's Cosmological Constant (or dark energy) acts like a repulsive force that pushes galaxies apart. As the universe expands, this force becomes stronger, causing the expansion to accelerate. This explains the observed speeding up of the universe's expansion.