Comprehensive CAT Formula Reference 2024

Sum of first n natural numbers

n(n+1)/2

Sum of squares of first n natural numbers

n(n+1)(2n+1)/6

Sum of cubes of first n natural numbers

[n(n+1)/2]^2

Sum of first n odd numbers

n^2

Dividend

(Divisor x Quotient) + Remainder

Profit Percentage

(Profit/Cost Price) x 100

Loss Percentage

(Loss/Cost Price) x 100

Selling Price

Cost Price + Profit

Selling Price (Loss)

Cost Price - Loss

Cost Price (Profit)

Selling Price - Profit

Cost Price (Loss)

Selling Price + Loss

Profit

Selling Price - Cost Price

Loss

Cost Price - Selling Price

Discount

Marked Price - Selling Price

Discount Percentage

(Discount/Marked Price) x 100

Marked Price (Selling Price)

Selling Price/(1 - Discount Percentage/100)

Marked Price (Cost Price)

Cost Price/(1 - Profit Percentage/100)

Profit Percent

Profit x 100 / C.P.

Loss Percent

Loss x 100 / C.P.

Selling Price (Profit)

Cost Price (100 + Profit%) / 100

Loss%

(x/10)²

Value of Loss

2x²S / (100² - x²)

HCF of A, B and C

The highest divisor which can exactly divide A, B, and C

LCM of A, B and C

The lowest dividend which is exactly divisible by A, B, and C

Other number

LCM x HCF / 1st number

HCF of fractions

HCF of the numerators / LCM of the Denominators

LCM of fractions

LCM of the numerators / HCF of the Denominators

Simple Interest (SI)

SI = Prt/100

Amount (A)

A = P + Prt/100 = P(1+rt/100)

Compound Interest (CI)

CI = A - P

Amount for Compound Interest

A = P(1+r/100)ⁿ

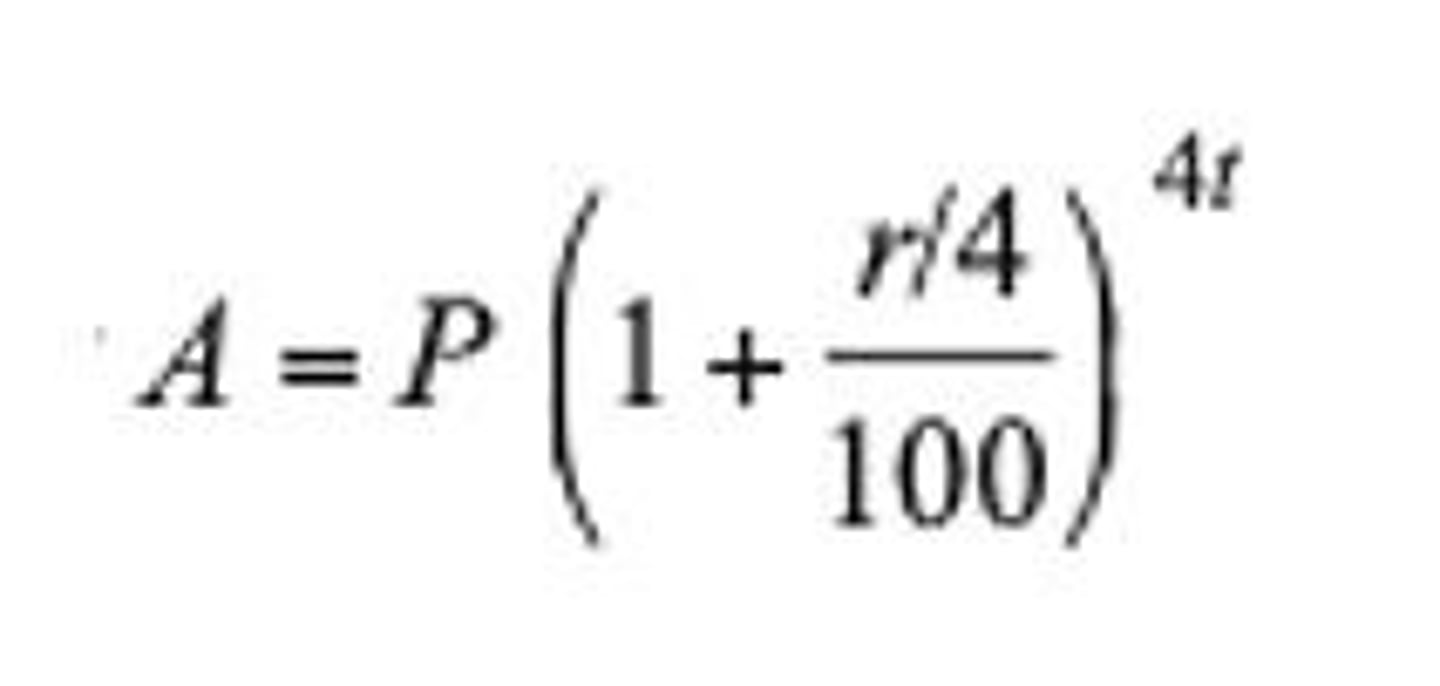
Half-yearly Compound Interest

A = P(1+r/2/100)²t

Quarterly Compound Interest

A = P(1+r/4/100)⁴t

Difference between CI and SI for two years

p(r/100)²

Difference between CI and SI for three years

p(r/100)² (r/100+3)

Depreciation

When the value of an item decreases in terms of currency

Initial value of the article (Vi)

The starting value before depreciation

Final value of the article (Vf)

The value after depreciation

Rate of interest (r)

The rate at which the price of article decreases over time period 't'

Work Done

Time Taken × Rate of Work

Rate of Work

1 / Time Taken

Time Taken

1 / Rate of Work

A's 1 day's work

1/n if A can finish the work in n days

Work done by A and B

1/x + 1/y if A can do work in x days and B in y days

Time taken by A and B

(xy) / (x + y)

Speed

Distance/Time

Average Speed

(Total distance travelled) / (Total time taken)

Distance

Speed X Time

Average

(Sum of observations) / (Number of observations)

New average after adding m numbers

(nA + mB) / (n + m)

New average after increasing each number by x

(nA + nx) / n

New average after decreasing each number by x

(nA - nx) / n

Product rule

a^m × a^n = a^(m+n)

Quotient rule

a^m / a^n = a^(m-n)

Power rule

(a^m)^n = a^(m×n)

Negative exponent rule

a^(-m) = 1 / a^m

Rational exponent rule

a^(m/n) = nth root of a^m

Fractional exponent rule

a^(p/q) = qth root of a^p

Surds multiplication rule

√a × √b = √(ab)

Surds division rule

√a / √b = √(a/b)

Logarithm definition

If x>0 and b is a constant (b≠1), then y = log bx if and only if x = by.

Logarithmic identity (product)

Log b(xy) = log bx + log by

Logarithmic identity (quotient)

Log b(x/y) = log bx - log by

Logarithmic identity (power)

Log b(x^p) = p log bx

Logarithmic identity (base)

Log b1 = 0

Logarithmic identity (same base)

Log bb = 1

Change of base formula

log b(x) = log a(x) / log a(b)

Common logarithm

log10(x) = log(x)

Natural logarithm

log e(x) = ln(x)

De Morgan's Law

(A ∩B)' = A' U B' and (A U B)' = A' ∩B'

Cardinality of a set

The number of elements in a set is called its cardinality.

Union of sets

A U B = {x: x ∈A or x ∈B}

Intersection of sets

A ∩B = {x: x ∈A and x ∈B}

Complement of a set

A' = {x: x ∉A}

Difference of sets

A - B = {x: x ∈A and x ∉B}

Cartesian product of sets

A × B = {(a, b): a ∈A and b ∈B}

n( A ∪B )

n(A) +n(B) - n (A ∩B)

n(A∪B)

n(A)+n(B) {when A and B are disjoint sets}

n(U)

n(A)+n(B)-n(A∩B)+n((A∪B)c)

n(A−B)

n(A∩B)−n(B)

n(Ac)

n(U)−n(A)

n(PUQUR)

n(P)+n(Q)+n(R)-n(P⋂Q)-n(Q⋂R)-n(R⋂P)+n(P⋂Q⋂R)

Commutative Laws

A B = B A

Associative Laws

(A B) C = A (B C)

Distributive Laws

A (B ∩C) = (A B) ∩(A C)

Identity Laws

A = A

Complement Laws

A Ac = U

Sine

Opposite/ Hypotenuse

Cosine

Adjacent/ Hypotenuse

Tangent

Opposite/ Adjacent

Secant

Hypotenuse/ Adjacent

Cosecant

Hypotenuse/ Opposite

Cotangent

Adjacent/ Opposite

Sum and Difference Formulas

sin(u + v) = sin(u)cos(v) + cos(u)sin(v)

Reciprocal Identities

cosec θ = 1/sin θ

Circumference of circle

2πr

Area of circle

πr2

Length of arc

θ/360×2πr

Area of Sector

θ/360×πr2

Area of Segment

θ/360×πr2-1/2×r2×sinθ