ENGR421 -Clustering

What is the purpose of EM

well assume you are given a dataset,

5 coin toss trials, and you know for each trial what the coin is, and the result, you can easily estimate the probability of heads for both coins using MLE, but what if you didn’t know what class each coin belonged to? Then how would you figure out the probability of heads for both coins, and the (hidden variable) a trial belonging to some class? This is where EM comes into play.

The non-mathematical example for EM

Well, obviously you start with some params, for the coin flip example lets say, pA (probability of coin A heads is ) = 0.6, and for B it is 0.4

then for all trials, you can get P(trial #x | coin A/B) using bayes rule

then with these you can do a soft count, for each trial and estimate again.

The matrix for EM.

here hik, is acutally the expectation of a data point belonging to some cluster (zik) (class whatever), given the current parameters.

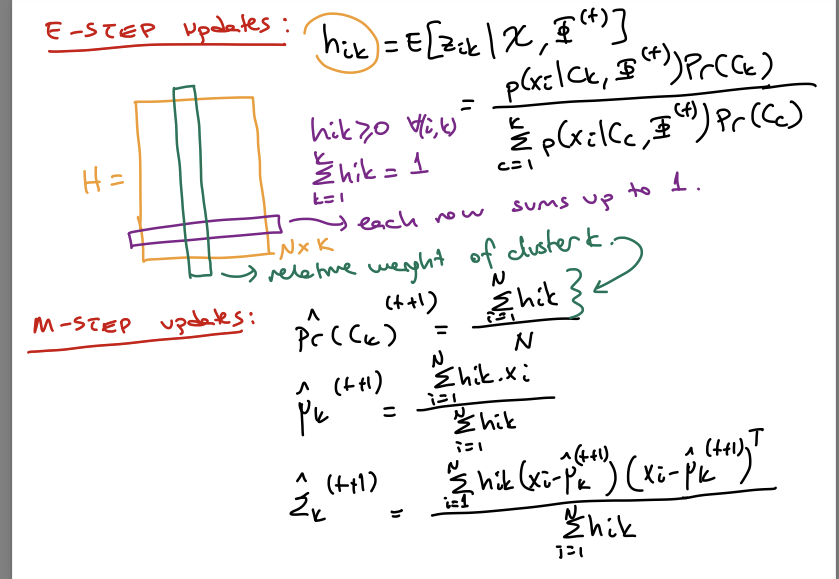
This is for reaching to four cards

a

k-means example from the book

assume you have a 8 bit screen where you can display at most 256 colors (you can pick these to be whatever you want from the 16 million colors from the 24 bit system)


the goal is to pick the best color mapping from 24 bit to 8 bit that best represents this image (color quantization)


best representation means, the most similar pixel for each color.

here each reference vector is a cluster,

and we try to minimize the reconstruction error

hierarchical clustering

we discussed clustering from a probabilistic pov as fitting a mixture model to the data, or in terms of finding code words minimizing the reconstruciton error,

but there are also methods for clustering that use only similarities of instances, without any other requirement on the data.

tha aim is to find groups such that instances in a group are more similar to each other than instances in different groups.

This is the approach taken by hierarchical clustering.

what you do in hierarchical clustering

well first of all you need to have a measure of similairty between instances or equivalently distance.

ie this can be the euclidian distance (special form of minkowksi distance with p = 2)

or city-block distance

but after being able to measure distances between instances, you also need to have a way of measuring distance between clusters

then you could have an algorithm that starts with N clusters, each cluster is a single instance, then you could merge the closes two and so on…

agglomerative clustering

starts with N clusters, each being a single instance, merging similar groups to form larger groups, until there is a single one.

divisive clustering

goes in the other direction of agglomerative clustering, starting with a single group and dividing large groups into smaller groups, until each group contains a single instance.

single link clustering

the distance between two clustes is the min possible distance between instances of each clusters

complete link clustering

distance between two groups is taken as the largest distance between all possible pairs

other ways of measuring distances between groups / clusters

centroid clustsering, average link (their names clearly explain the methods)

once an agglomerative method is run, the result is generally drawn as a hiearchical structure known as

the dendogram

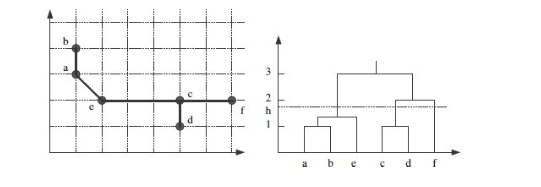
the problem with single link chaining

can cause chaining effect.

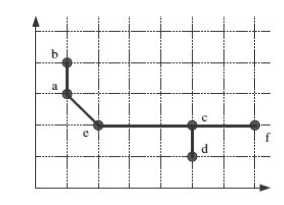
like assume there was an instance between e and c,