Plane Geometry

Geometry

It was derived from the Greek words “ge” meaning earth and “metria” meaning measurement

Plane Geometry

it deals with the properties of plane figures or geometrical shapes of two dimensions, such as angles, triangle, square, polygons, conic sections, etc.

Solid Geometry

Deals with the properties of geometrical shapes of three dimensions, such as cones, pyramids, cylinders, prisms, spheres, etc.

Euclidean Geometry

a geometry that is based on the assumptions of Euclid.

Non-Euclidean Geometry

a geometry that is not based on the assumption of Euclid

Projective Geometry

deals with the study of those properties of plane figures that are unchanged when a given set of points is projected onto a second plane

Trigonometry

a geometry which specializes on the study of triangle

Analytical Geometry

a geometry which deals with geometric problems by using the coordinates system and transforming them into algebraic problems

Differential Geometry

a geometry that applies differential and integral calculus to curves, surfaces and other geometric entities

Basic Postulates of Euclid (Parallel Postulate)

Point

a dimensionless geometric figure having no properties other than location or place

Line

the shortest distance between any two points.

Angle

the opening between two lines or two planes that meet

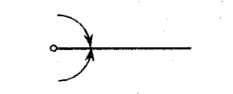
Null or Zero Angle

angle equal to 0

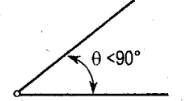
Acute Angle

angle greater than 0 but less than 90deg or pi/2 rad

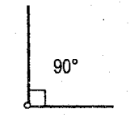
Right Angle

angle equal to 90 deg or pi/2 rad

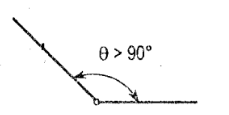
Obtuse Angle

angle greater than 90deg or pi/2 rad but less than 180deg or pi rad

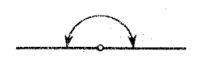
Straight Angle

angle equal to 180deg or pi rad

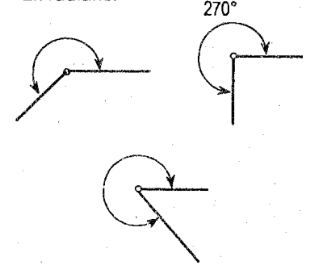
Reflex Angle

angle greater than 180deg or pi rad but less than 360deg or 2pi rad

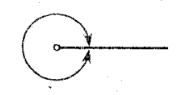
Full angle or Perigon

angle equal to 360deg or 2pi rad

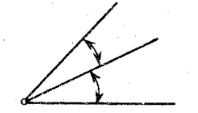
Adjacent Angles

two angles with a common leg

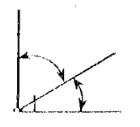
Complementary Angles

two angles whose sum is a right triangle (90deg)

Supplementary Angles

two angles whose sum is a straight angle (180deg)

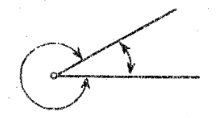
Explementary Angles

two angles whose sum is a perigon (360deg)

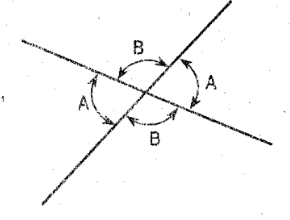
Vertical Angles

angles formed by two intersecting lines.

Bisector

it is a straight line which divides a geometric figure into two equal figures

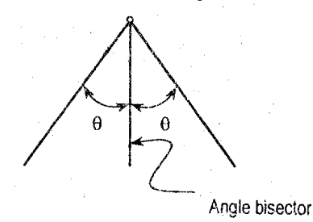
Angle Bisector

it is a line which divides an angle into two equal angles

Different Unit of Angles

Regular Polygon

it is a polygon having all sides equal and all angles equal

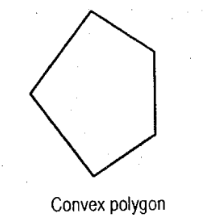
Convex Polygon

it is a polygon having interior angle less than 180deg

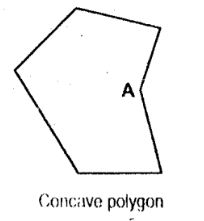
Concave Polygon

it is a polygon having an interior angle greater than 180deg

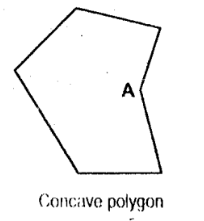
Reentrant Angle

it is the inward-pointing angle (A) of the concave polygon

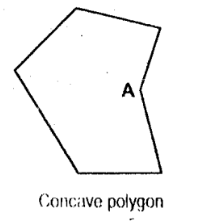
Salient Angle

it is the outward-pointing angle of the concave polygon

Diagonal

it is the line in a polygon connecting two opposite vertices

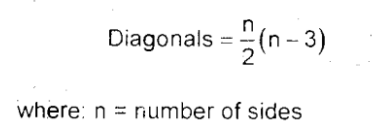
Number of Diagonals = (n/2) (n-3)
Where:
n = number of sides

formula derivation:
Square: 4 Sides; 2 Diagonals

Number of Diagonals Formula:

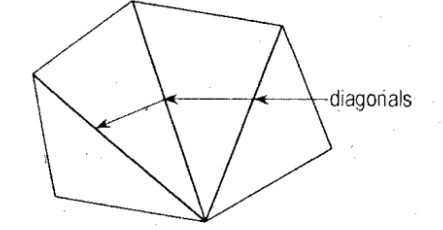
Sum of Interior Angles = (n-2) 180deg
Where:
n = number of sides

formula derivation:
Triangle: 3 Sides; Sum of interior angles 180deg

Sum of Interior Angles Formula:

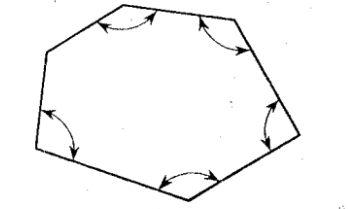
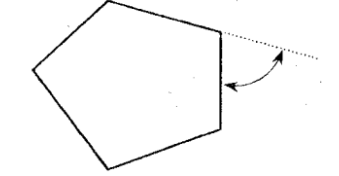
Deflection Angle

it is the angle subtended on a polygon by the prolongation of the side to the next side

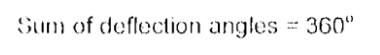
360deg

Sum of Deflection Angles:

Triangle

it is a polygon with three sides

Classifications of Triangle according to their Sides:

Classifications of Triangles according to their Angles:

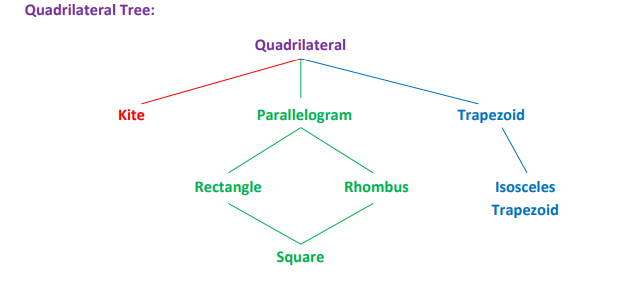
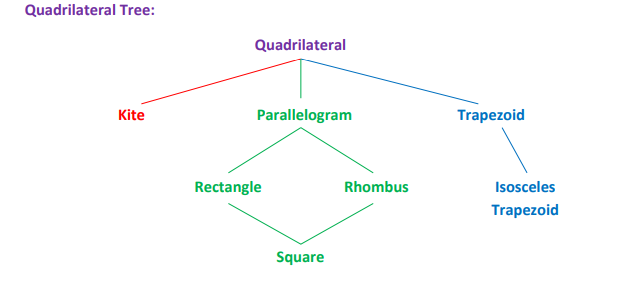
Quadrilateral (quadrangle or tetragon)

It is a polygon with four sides

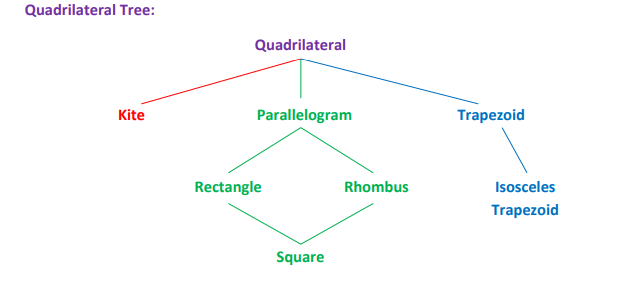
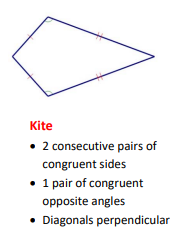
Kite

A quadrilateral with two consecutive pairs of congruent sides, but with opposite sides not congruent.

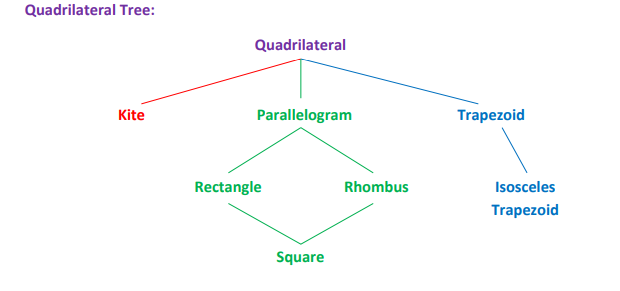
Trapezoid

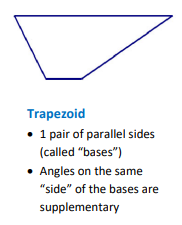
A quadrilateral with exactly one pair of parallel sides.

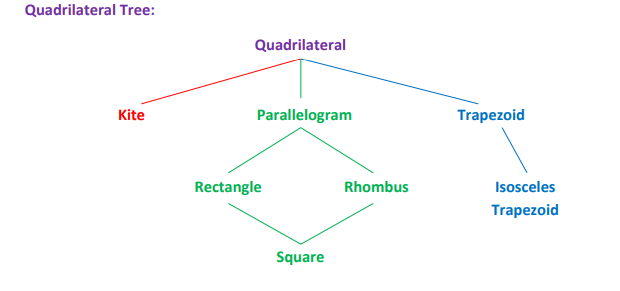
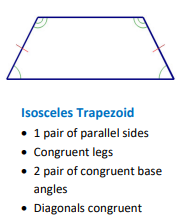
Isosceles Trapezoid

A trapezoid with congruent legs.

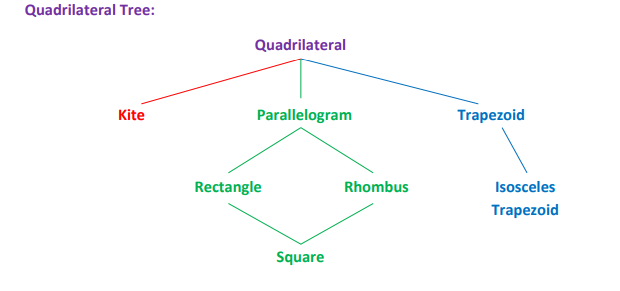
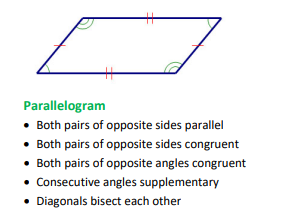
Parallelogram

A quadrilateral with both pairs of opposite sides parallel.

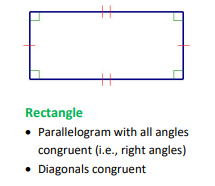
Rectangle

A parallelogram with all angles congruent (i.e., right angles).

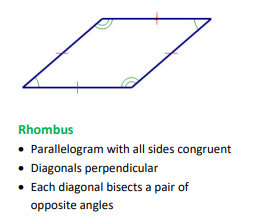
Rhombus

A parallelogram with all sides congruent.

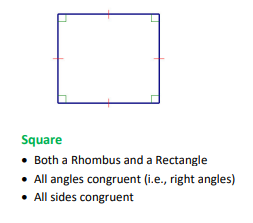
Square

A quadrilateral with all sides congruent and all angles congruent.

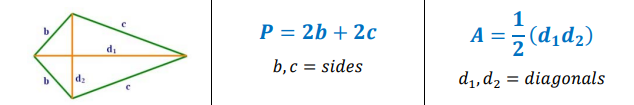
Perimeter and Area of a Kite

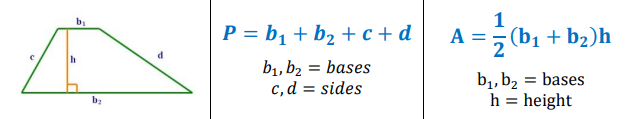
Perimeter and Area of a Trapezoid

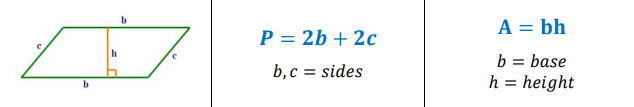
A = ½ (d₁)(d₂) sin(theta) = bc sin(theta)

Perimeter and Area of a Parallelogram

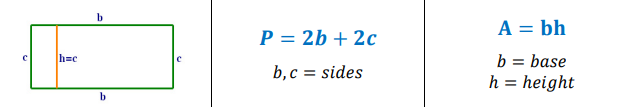
Perimeter and Area of a Rectangle

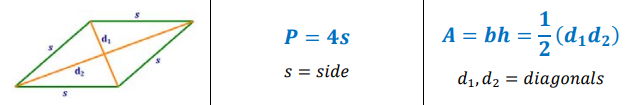
A = s² sin (theta)

Perimeter and Area of a Rhombus

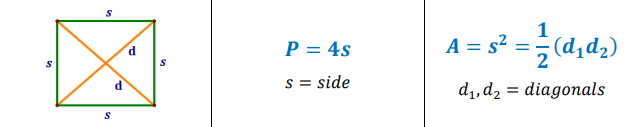
Perimeter and Area of a Square

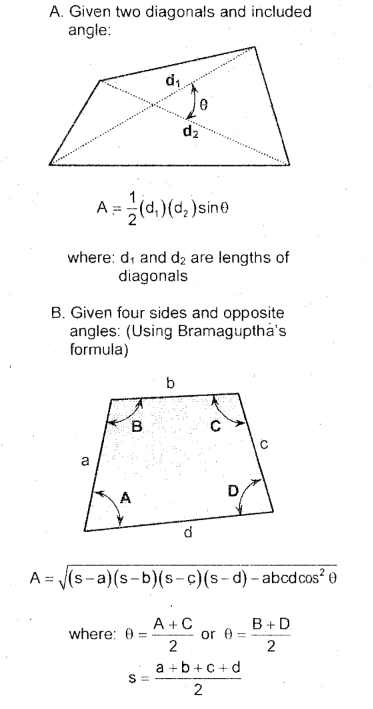
Heron’s Formula & Bramaguptha’s Formula alike
theta = median of opposite angles
semi-perimeter = sum of sides/2

Area of a Trapezium (General Quadrilateral)

Area of Cyclic Quadrilateral

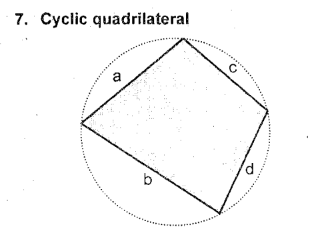
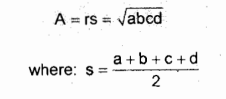
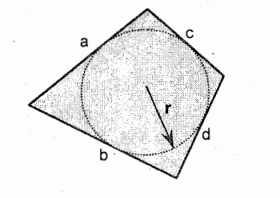
Area of Quadrilateral Circumscribing a Circle

Bramaguptha’s Theorem

"In a cyclic quadrilateral having perpendicular diagonals, the perpendicular to a side from the point of intersection of the diagonals always bisects the opposite side"

Ptolemy’s Theorem

"The sum of the products of two pairs of opposite sides of a convex cyclic quadrilateral is equal to the product of the lengths of the diagonals."

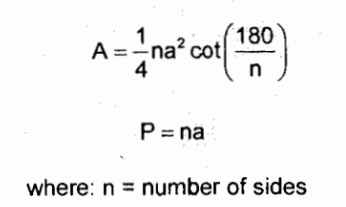
A = (na²)/(4 tan(180/n))
P = na

Perimeter and Area of a Regular Polygon

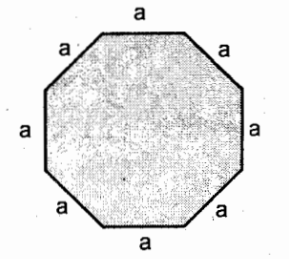
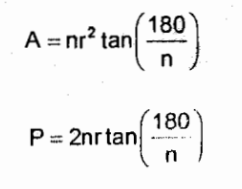
A = nr² tan (180/n)
*looks alike with Area of circle with pi as n and multiplied with tan(180/n)

P = 2nr tan (180/n)
*looks alike with Perimeter of circle with pi as n and multiplied with tan(180/n)

Perimeter and Area of a Regular Polygon Circumscribing a Circle

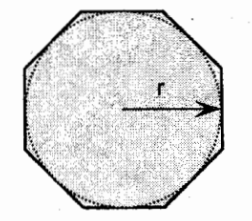
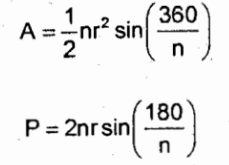
A = ½ nr² sin(360/n)
*looks alike with Area of circle with pi as n and multiplied with ½ sin(360/n)

P = 2nr sin(180/n)
*looks alike with Perimeter of circle with pi as n and multiplied with tan(180/n)

Perimeter and Area of a Regular Polygon Inscribed in a Circle

Perimeter

it is a distance around a two-dimensional shape

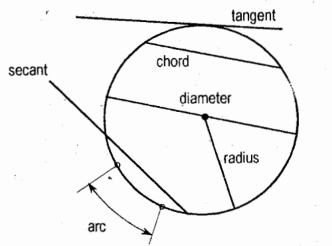
Circle

it is a plane curve that is the locus of all points in the plane equidistant from a given point, called center.

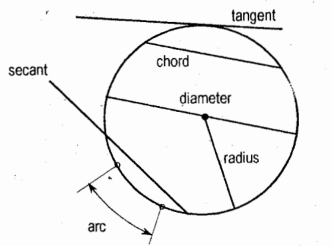
Arc of a Circle

it is the length of circle between two points on the circle or between two radii

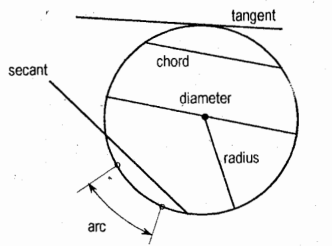
Tangent of a Circle

it is a line touching the circle in one place

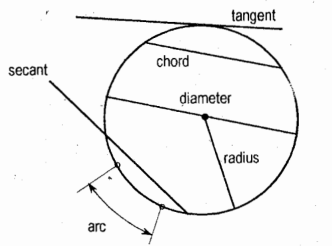
Secant of a Circle

it is a line cutting the circle in two places

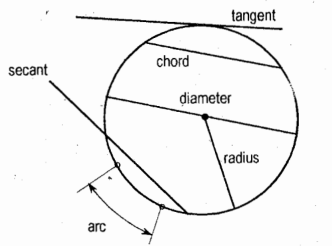
Diameter of a Circle

It is the longest chord of a circle that passes through the center

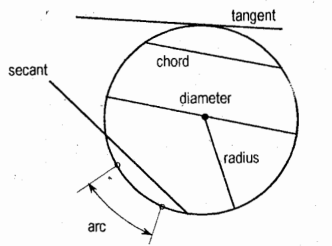
Radius

it is the distance from the center to the circle
it is ½ of the diameter

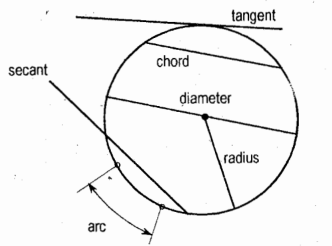
Chord

it is the segment of a secant bounded by the circle

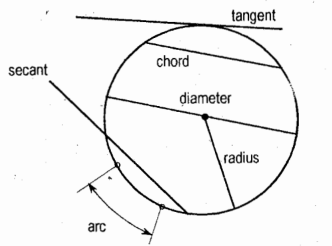
Circumference (Periphery)

it is the perimeter of a circle

Radian

it is the measure of an angle whose arc length is equal to the radius of a circle

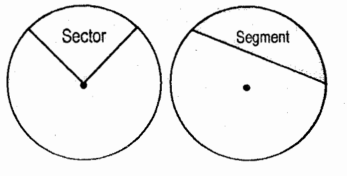
Sector of a Circle

it is the area bounded by two radii and the included arc

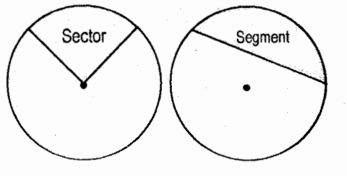
Segment of a Circle

it is the area bounded by a chord and the arc subtending the chord

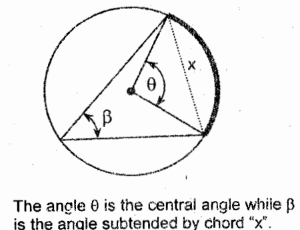
Central Angle

it is an angle whose vertex is at the center of a circle and whose sides are the radii

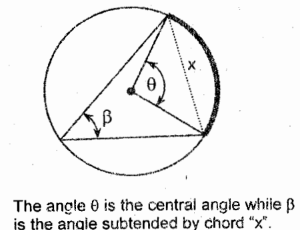
Angle subtended by a Chord

it is an angle whose vertex is along the periphery or circumference and its sides are chords

Area and Circumference of a Circle

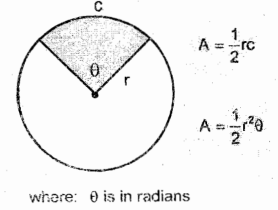
Area of Sector of a Circle

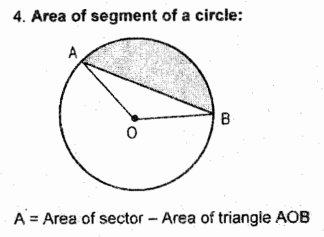
Area of Segment of a Circle

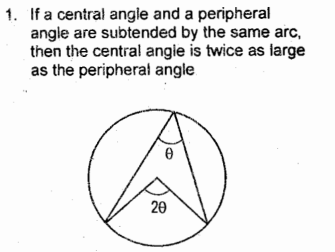
Relation of Central Angle and Peripheral Angle

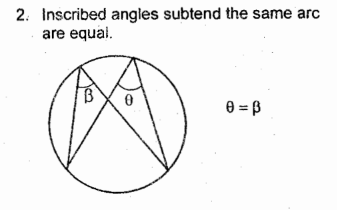
Inscribed Angles subtended the same Arc

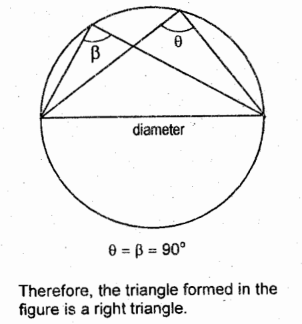
Inscribed Angles subtended by the Diameter

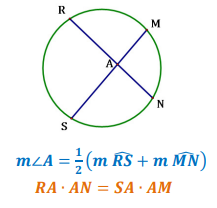
Vertex Inside the Circle

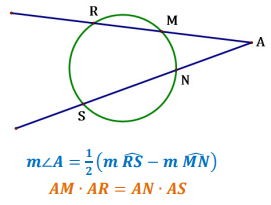
Vertex Outside the Circle

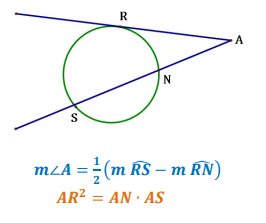
Tangent on One Side

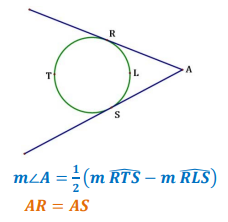
Tangent on Two Sides

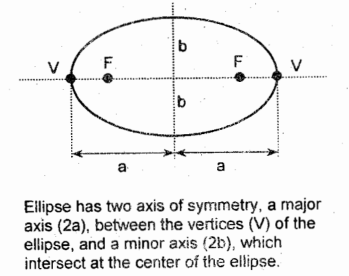
Ellipse

it is a locus of a point which moves so that the sum of its distances to the fixed points is constant and is equal to the length of the major axis

A = (pi)(a)(b)
*looks alike with the Area of a Circle but replacing r² with ab

Area of an Ellipse