7 & 8. Population Growth

Population size

number of individuals of same species living in a defined geographical area

Population sizes change

• births-deaths

• + immigrants-emigrants

Geometric and exponential models describe…

populations growth in an idealized environment with unlimited resources and good constions

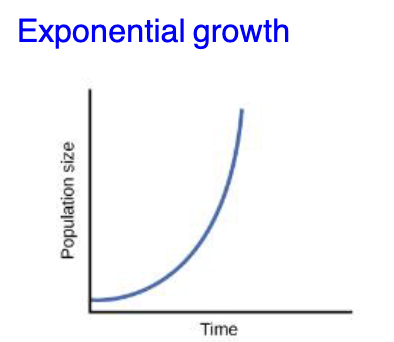
Exponential growth

growth exponentially

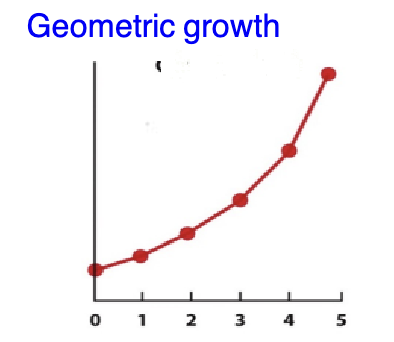
Geometric growth

discrete time intervals

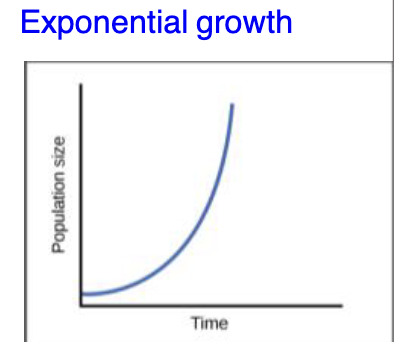
Unregulated growth

Exponential growth

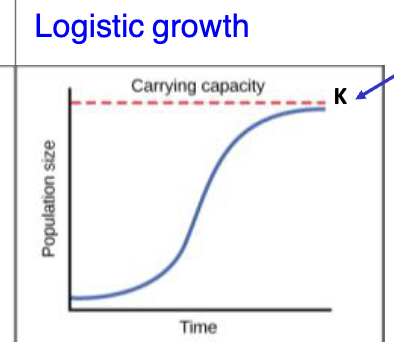
Regulated growth

Logistic growth

If there are limiting factors/resources

Population growth rate

number of new individuals that are produced per unit of time mins the number of individuals that die

Intrinsic growth rate (r )

• highest possible per capita growth rate for a population (maximum reproductive rates & minimum death rates)

• For a closed population (with no migration) r = b -d

• r = birth rate (b) - death rate (d)

• r (+ (growing)) (- (decreasing))

Intrinsic growth rate example

• population of 100 bats, in one year 80 born, 60 dies

• r = b-d

• b = 80/100 individuals = 0.8

• d = 60/100 individuals = 0.6

• r = 0.8-0.6 = 0.2 (population is growing)

Exponential growth model

• model of population growth in which population increases continuously at an exponential rate; described by equation

• Nt - N0 e ^rt

• Nt = future population size

• N0 = current population size

• e = exponential constant 2.72

• r = intrinsic growth rate

• t = time over which a population grows

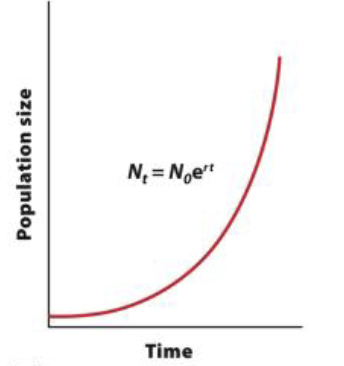
Exponential population growth

• The shape of the growth when graphed is a J-shaped curve

• The rate of the a population’s growth at a point in time is

• G = rN

• G = number of individuals added during any time interval

• r = intrinsic growth rate: b - d

• N = population size

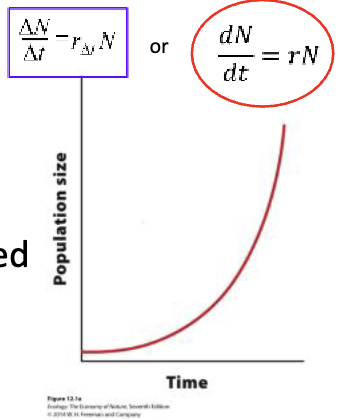
In exponential growth

• The shape of the growth when graphed is a J-shaped curve

• G = number of individuals added during time (growth increment)

• G = r * N

• growth rate * population

• if isolate r: r = G/N

Exponential growth example

We have 100 aquatic beetles with r = 0.22 per day. How many individuals will be added per day?

• 100 aquatic beetles with r = 0.22 per day

• G = 0.22 × 100 = 22. individuals per day

• New aquatic beetles will eventually and more offspring to the existing population

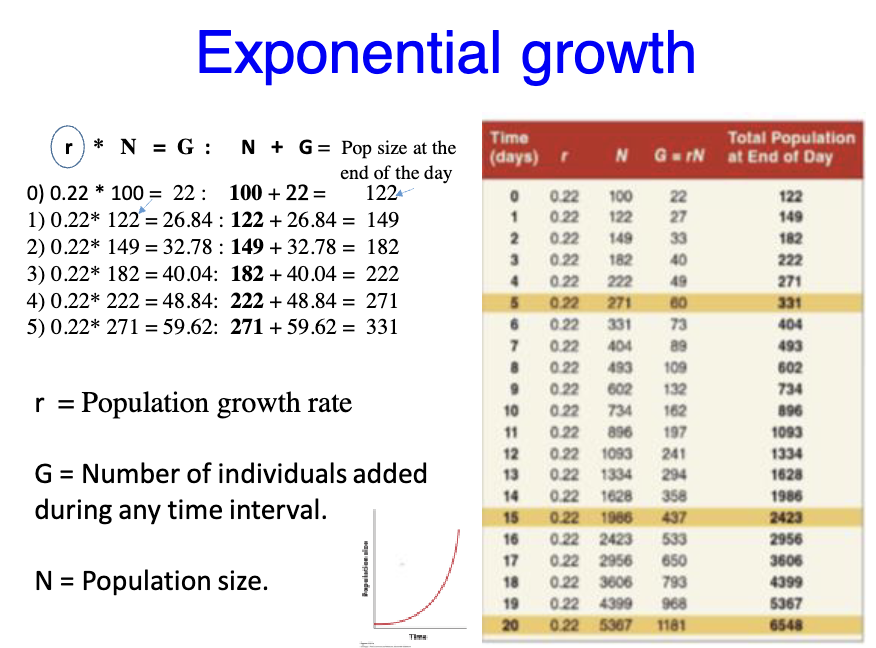
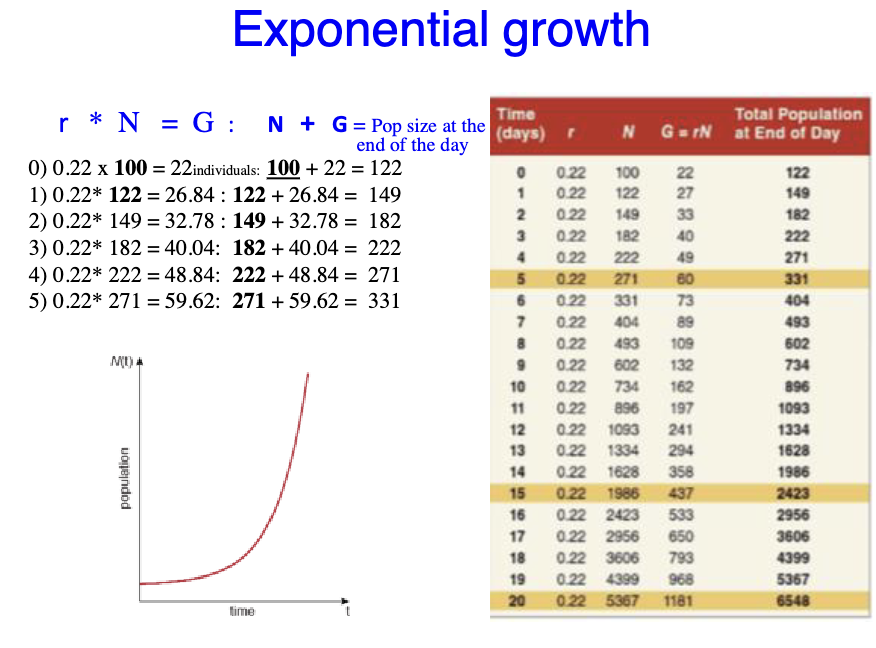
Exponential growth rate example #2

• We have 100 aquatic beetles with r = 0.22 per day. How many individuals will be added the first day and how many individuals you will have after one, two, and three days?

• G = rN

• New population size N + G

• r = Population growth rate

• G = Number of individuals added during any time interval

• N = Population size

Geometric growth model

• compares population size at regular time intervals

• used for species with discrete

• expressed as a ratio of a population’s size in one year to its size in preceding year (λ)

• λ cannot be negative

• λ > 1, population size has increased

• λ = 180/100 =1.8

• λ < 1, population size has decreased

• λ = 80/100 = 0.8

Geometric growth model info

• size of a population after one time interval is:

• N1 = N0λ

• size of a population after time intervals, the population size would be

• N2 = (N0λ)λ = N0λ²

• More generally, after t time intervals

• Nt = N0λ^t

Comparing growth models

• When a population is decreasing, λ < 1 and r < 0

• When a population is constant, λ > 1 and r = 0

• When a population is increasing, λ > 1 and r > 0

• r for exponential growth

• λ for geometric growth

Population regulation (controls)

• Density dependent controls: Effects increase as population grows. Infraspecific competition, predation, parasitism and infectious disease

• Higher population size = food supply diminishes competition increases

• Higher density = predators are attracted

Population regulation (controls)

• Density dependent controls: effects increase as population grows: intraspecfic competition, predation, parasitism, & infectious disease

• Higher population size = food supply diminishes

• Higher density = infectious diseases spread more easily

• Higher density = predators are attracted

Density-dependence in plants

Resources: sunlight, water, soil nutrients, etc.

Ex: horseweed plants at a density of 100,000 m² over time, many individuals dies.

As density decreased, there was a significant increase in the weight of surviving individuals

Postitive density dependence

Rate of population growth can increase as population density decreases (inverse density dependence or Allee effect)

Decline in individual population size or density

Postive correlation between population density & individual fitness

Population regulation

• Density independent controls: Limit population size regardless of populations’s density

• Climatic events (e.g. tornadoes, floods, extreme temps, droughts, fire, etc.)

• Birth & death rates do not change as density rises, but suddenly mortality rate increases, reproductive rate decreases

Logistic growth model

The per capita rate of population growth approaches zero as the population size nears carrying capacity (K)

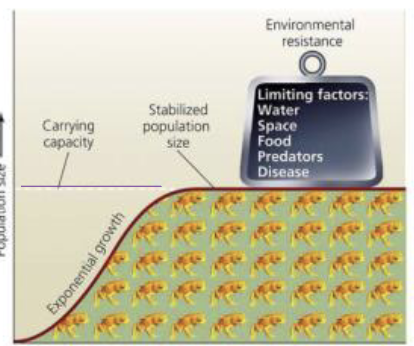
Logistic population growth

density dependent factors are in effect

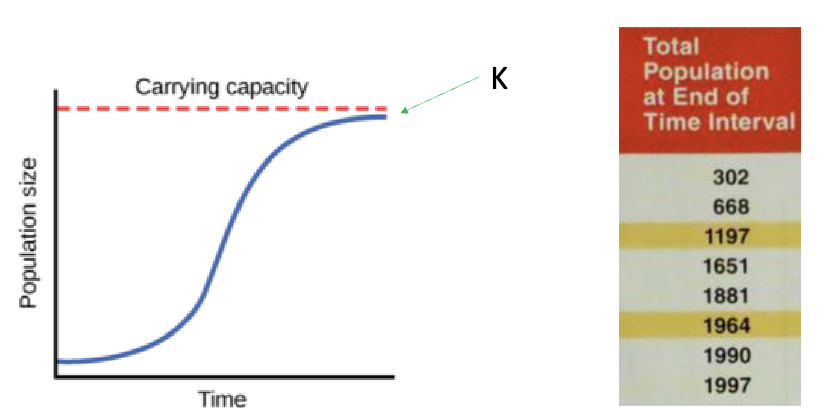
logistic growth model equation

• Growth of populations at high densities:

• dN/dt = rN (1-N/K)

Logistic growth in general

• G = rN (K-N/K)

• G = number of individuals added per unit of time (growth increment)

• r = growth rate

• N - number of individuals in the population at a given time (population size)

• K = Carrying capacity

Carying capacity (K)

• The maximum population size that can be supported by the environment

• As the population size increases:

  • Resource shortages

  • Environmental limitations

  • within-species competition

• imposes an upper limit on a population’s size

• typically is not fixed (can change at some point)

Logistic growth graphs

S- shaped curve: shape of the curve when a population is graphed over time using the logistic growth model

Inflection point: the point on a sigmoidal growth curve at which the population has its highest growth rate

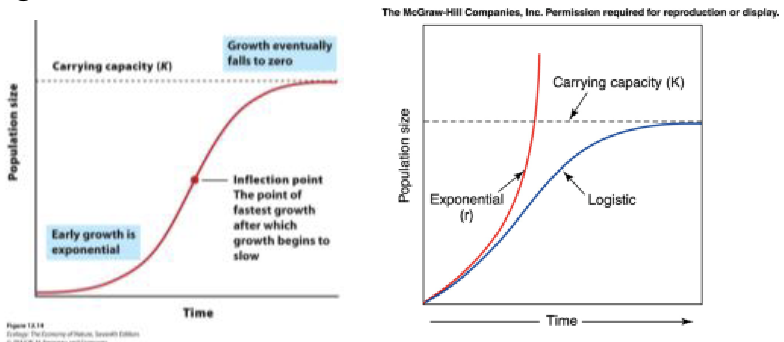
Logistic growth model example

• two species of protists with a fixed amount of food each day

• Populations initially grew in size, but eventually stabilized at different carrying capacities dependent on the available resources

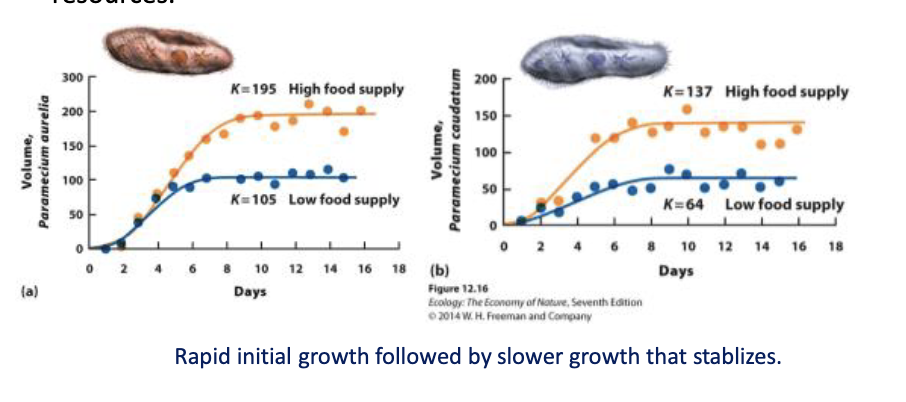
Is the following population exhibiting logistic growth?

If so, what is the carrying capacity?

no

Is the following population exhibiting logistic growth?

If so, what is the carrying capacity?

no

Is the following population exhibiting logistic growth?

If so, what is the carrying capacity?

Yes, 157

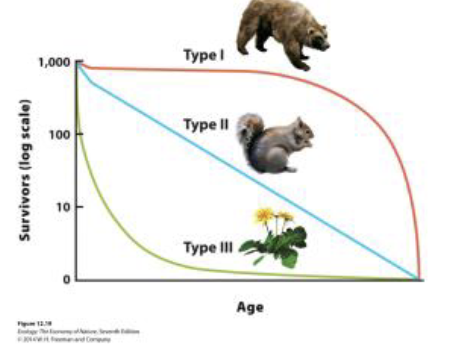
Survivorship curves

• Type 1: low mortality early in life, & high mortality later in life (large mammals)

• Type II: Constant mortality throughout the life span (different birds, squirrels, corals). Stead decline in survival throughout life

• Type III: High mortally early in life and high survival later in life (weeds)

Life table

• Class-specific survival and fecundity data

• based on number of female offspring per female

• x = age class

• nx = number of indi

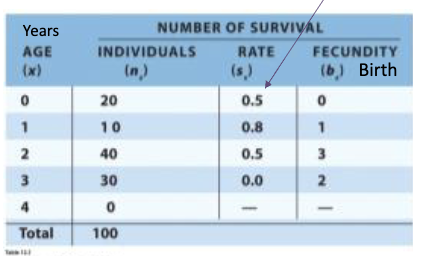
Life table calculations

• Number surviving to net age class = (nx) (sx)

• Number of offspring produced (nx) (sx) (bx)

• λ: number of individuals in a population after one interval divded by the initial number of individuals

• λ = N1/N0 =

Surviviorship

Probability of surviving from birth to any later age class (/x); surviorhsip in the first age class is always set a 1.

ex: for second year (I2) would be I2 = /1 s1

A mammalogist estimates that there are N1 =
10,000 mice living in a large section of forest,
which she estimates has a carrying capacity (K) of
100,000. The population appears to have an
intrinsic growth rate (r) = 0.05 mice / mouse / year
What do you predict for G during this next year?
a) 45 mice
b) 50 mice
c) 450 mice
d) 500 mice
e) 4500 mice

c) 450 mice

A mammalogist estimates that there are N1 =
10,000 mice living in a large section of forest,
which she estimates has a carrying capacity (K)
of 100,000. The population appears to have an
intrinsic growth rate (r) = 0.05 deer mice / deer
mouse / year
What do you predict for G during this next year?
a) 45 mice
b) 50 mice
c) 450 mice
d) 500 mice
e) 4500 mice

G = rN (K-N/K)

c) 450 mice

A mammalogist estimates that there are N1 =
10,000 mice living in a large section of forest,
which she estimates has a carrying capacity (K)
of 100,000. The population appears to have an
intrinsic growth rate (r) = 0.05 deer mice / deer
mouse / year
What do you predict for G during this next year?
a) 45 mice
b) 50 mice
c) 450 mice
d) 500 mice
e) 4500 mice