ALL PHYSICS FORMULAS

electic current (I)

I= ΔQ/Δt

• units C/s or A

ohm’s law

V=IR

power dissipated by resistor

P= IV=V²/R=I²R=Energy/t

resistance (R)

R=(ρL)/A

kirchoff’s rules

1. ΣV=0 (loop rule)

2. ΣI_in=I_out (junction rule)

capacitator charge

Q=CV

dielectrics and capacitors equations

energy stored in capacitors

U_c=1/2QV=1/2C(V)²=1/2(Q²/C)

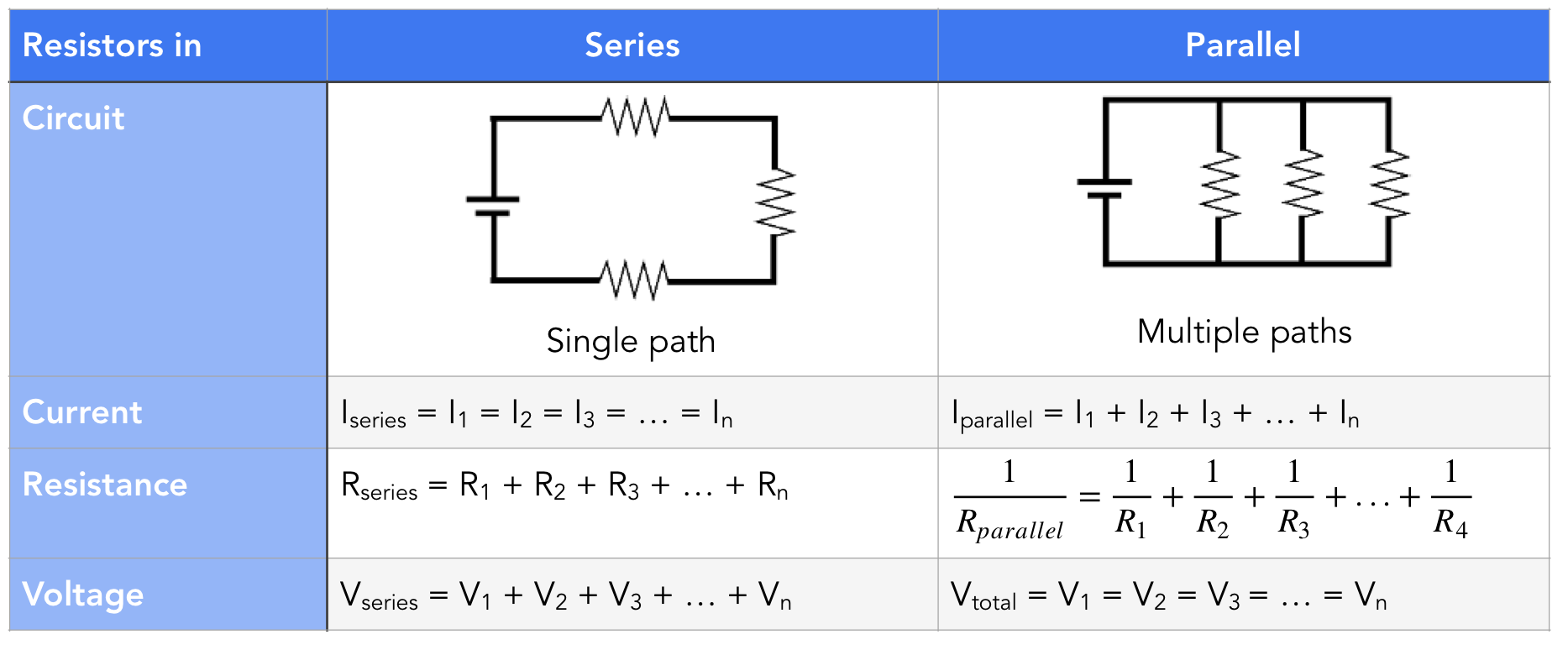
resistors in series and parallel

polarization

the separation of positive and negative charges within an object

what is the difference between conductors and insulators?

conductors allow charges to move through them easily while insulators do not

law of conservation of electric charge

total electric charge in an isolated system is constant

coulomb (C) or elementary charge (e)

1.60 × 10^-19

couloumbs law

• electrostatic force between two charged particles

• k= constant of proportionality= 9 × 10⁹ Nm²/C²

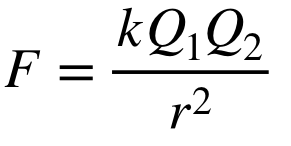
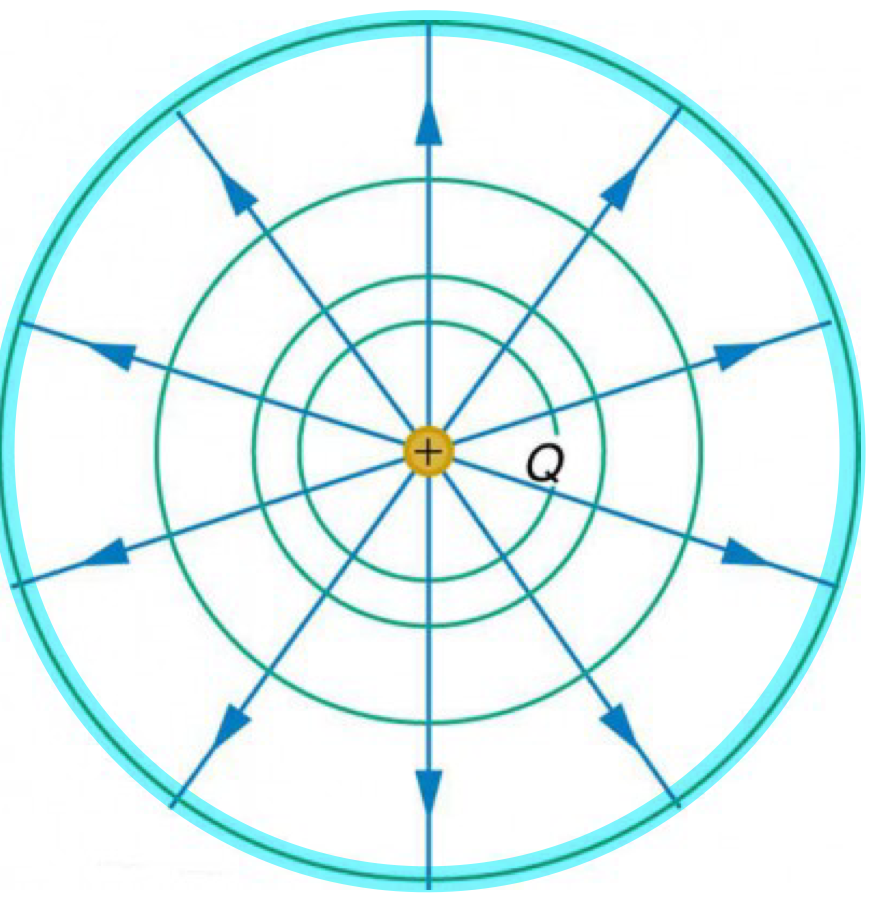
magnitude of electric field

r= distance between source and test charge

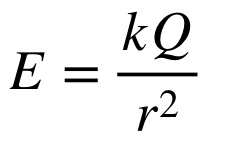
which direction does an electric field point?

the electric field vectors point AWAY from POSITIVE charges and TOWARDS NEGATIVE charges

properties of electric field charges

1. direction from + charge towards - charge

2. number of field lines drawn ansd closeness of lines indicates strength of the field

electric field vs electrostatic force on a charge within the field equation

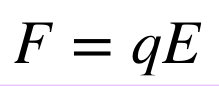
electric potential

the energy needed to move a charge in an electric field from one point to another

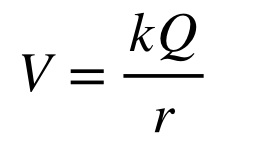
equipotential lines

indicate the electric potential at any given point around a charge in an electric field

electric potential energy (withina. field)

energy stored in a charged object due to its position within an electric field

• change in electric potential energy between two points

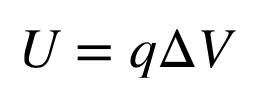
work done by an electric field

amount of electric potential energy that is changed (dependent only on the initial and final locations of the potentials)

W>0 charge moves in the direction of electric field (higher to lower potential)

W<0: charge moves opposite direction of electric field (low to high potential)

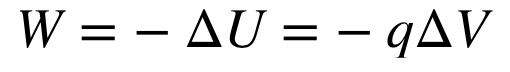
electric potential energy (between two charges)

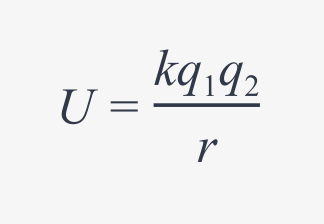
electric field strength

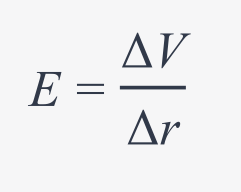
prefixes and symbols for 10¹² to 10¹²

10¹²: Tera (T)

10⁹: Giga (G)

10⁶: Mega (M)

10³: Kilo (k)

10^-2_: Centi ©

10^-3: Mili (m)

10^-6: Micro (μ)

10^-9: Nano (n)

10^-12: Pico (p)

sin, cos, tan of 0

sin: 0

cos: 1

tan: 0

sin, cos, tan of 30

sin: 1/2

cos: √3/2

tan: √3/3

sin, cos, tan 37

sin: 3/5

cos: 4/5

tan: 3/4

sin, cos, tan 45

sin: √2/2

cos: √2/2

tan: 2

sin, cos, tan 53

sin: 4/5

cos: 3/5

tan: 4/3

sin, cos, tan 60

sin: √3/2

cos: 1/2

tan: √3

sin, cos, tan 90

sin: 1

cos: 0

tan: infinity

proton mass (m_p)

m_p=1.67 × 10^-27 kg

neutron mass (n_p)

m_n=1.67 × 10^-27 kg

electron mass (m_e)

m_e= 9.11 × 10^-31 kg

electron charge magnitude

e=1.6 × 10^-19 C

1 electron volt

1 ev=1.6 × 10^-19 C

speed of light ©

c= 3 × 10⁸ m/s

universal gravitational constant

G= 6.67 × 10^-11 m³/(kg x s²)

acceleration due to gravity at Earth’s surface

g=10 m/s²

avogadro’s number

N_A=6.02 × 10²³ mol^-1

universal gas constant (2 kinds!)

R= 8.314 J/mol x K

R= 0.0821 L atm/ mol K

boltzmann’s constant

K_B= 1.38 × 10^-23 J/k

relationship between L x Pa and J

1 L x Pa = 0.001 J

relationship between L and m

1 L= 0.001 m³

relationship between cm³ and m³

1 cm³= 1 × 10^-6 m³

examples of vector quantities

1. displacement

2. velocity

3. acceleration

4. force

5. torque

6. momentum

7. electric field

8. weight

examples of scalar quantities

1. distance

2. speed

3. work/energy

4. power

5. presure

6. electric potential

7. temperature (but can be positive or negative)

8. density

9. mass

displacement equations

Δx=v_i(t)

Δx= Δx₀ + v_i(t) + 1/2a(t)²

final velocity equations

v_f=v_i+ a(t)

(v_f)²=(v_i)² + 2aΔx

displacement

average velocity

v_avg= (v_i+v_f)/2

projectile horizontal displacement

Δx= v_i,x(t)

projectile max height

H_max= (v_i,y)²/2g

projectile max range

R= ((v_i)² (sin 2θ))/g

projectile total flight time

t= 2v_i,y/g

net force

F_net=ma

newton’s 3rd law

-F₁=F₂

friction

f=μF_N

static friction

f_s</= μ_sF_N

kinetic friction

f_k= μ_kF_N

tension of two blocks connected by a rope

SAME

torque

τ=rFsinθ

+= CCW

-= CW

critical point

point where center of gravity is no longer directly above the base of support

stable equilibrium

if displaced, returns back to original position (cg remains within the base of support)

unstable equilibrium

if displaced, it does not return to its original position (cg is outside the base of support)

neutral equilibrium

if displaced, it remains in its new positio (such as a ball placed on a horizontal position)

static equilibrium

state of equilibrium where an object is at rest

dynamic equilibrium

state of equilibrium where an object is moving at constant velocity

x-component of force

F_x=Fcosθ

y-component of force

F_y=Fsinθ

magnitude of force

F= √(F_x)²+(F_y)²

unknown angle of force

tanθ= F_y/F_x

weight

F_g=mg

kinetic energy

KE=(1/2)mv²

linear momentum

p=mv

impulse

Δp=FΔt

kinetic energy/work theorem

W_net=ΔKE=(1/2)mv_f²-1/2)mv_i²

W=F||d=Fdcosθ

power

P=ΔE/Δt=W/t=Fv

center of mass

x_cm=Σm_ix_i/Σm_i

mechanical energy

E= KE + U_G

gravitational potential energy

U_G= mgh

conservation of mechanical energy

ΔE= ΔKE + ΔU = -W_fr

efficiency

e=W_out/E_in

hooke’s law

F_x=-kx

spring potential energy

U=(1/2)kx²

period of simple harmonic oscillator

T_s= 2π√m/k

frequency of simple harmonic oscillator

f=1/2π√k/m

angular frequency

ω=2π/T=√k/m=2πf

max speed of a spring

v_max= Aω

max acceleration of a spring

a_max=Aω²

period of a simple pendulum

T_p= 2π√L/g

frequency of a simple pendulum

f=1/2π√g/L

position of simple harmonic motion

x=Acos(ωt)=Acos(2πft)

wavelength

λ=v/f

malus law

I=I₀cos2θ

intensity of sound

dB=10log₁₀(I_i/I₀)

frequency of string attached at both ends

f= nv/2L

frequency of pipe open at both ends

f= nv/2L

frequency of pipe open at one end

f= nv/4L

*note: harmonics is odd numbers