Chapter 26: The Special Theory of Relativity

inertial reference frame

a frame of reference that is moving at a constant velocity

a reference frame that moves with constant velocity with respect to an inertial frame is...

itself an inertia frame

relativity principle

The basic laws of physics are the same in all inertial reference frames.

*but paths may be different in different reference frames

Galilean-Newtonian relativity assumed that...

the lengths of objects are the same in one reference frame as in another, and that time passes at the same rate in different reference frames

in classical mechanics, then, space and time intervals are considered to be

absolute

absolute

their measurement does not change from one reference frame to another

the mass of an object, as well as all forces, are assumed to be ________ by a change in inertial reference frame

unchanged

the position of an object is _______ when specified in different reference frames

different

the velocity of an object is _______ when specified in different reference frames

different

according to classical mechanics, the acceleration of an object is...

the same in any inertial reference frame
*bc the change in velocity, and the time interval, will be the same

all inertial reference frames are equivalent;

no single inertial reference frame is any better than another

in what reference frame does light have precisely the value predicted by Maxwell's theory?

Maxwell's equations have no provision for relative velocity

ether

light must travel in some medium

first postulate of special relativity

The laws of physics have the same form in all inertial reference frames.

second postulate (constancy of the speed of light)

Light propagates through empty space with a definite speed c independent of the speed of the source or observer.

according to relativity, the time interval between two events, and even whether or not two events are simultaneous, depends on...

the observer's reference frame

event

something that happens at a particular place and at a particular time

two events which take place at different locations and are simultaneous to one observer...

are actually not simultaneous to a second observer who moves relative to the first

simultaneity is not an ______ concept

absolute

time dilation effect

clocks MOVING relative to an observer are measured to run more SLOWLY, as compared to clocks at rest


**time is actually measured to pass more slowly in any moving reference frame
as compared to your own

time interval between the two events as measured in a reference frame moving with speed v with respect to the first

∆t

time interval between the two events in a reference frame where an observer at rest sees the two events occur at the same point in space

∆t0

γ

never less than 1
has no units

time dilation effect is negligible unless....

v is reasonably close to c

(if v is much less than c, then v2/c2 is much smaller than 1, and then ∆t≈∆t0

time dilation equation (∆t=∆t0/√1-v2/c2), ∆t=γ∆t0
only true when

∆t0 represents the time interval between two events in a reference frame where an observer at rest sees the two events occur at the same point in space

proper time

∆t0
time interval between two events that occur at the same position
**shortest time between the events any observer can measure

binomial expansion

use to estimate difference between ∆t and ∆t0

(1±x)^n ≈ 1±xn for x<<1

space travel

All processes, including aging and other life processes, run more slowly for the astronaut as measured by an Earth observer. But to the astronaut, time would pass in a normal way

Twin Paradox

different observers' measurements of the time taken for a journey at speeds close to the speed of light will not be the same

(NOTE: Since one of the twins has to accelerate in the spaceship, this is no longer a symmetrical situation for the twins. The space journeying twin records a shorter time measurement ("ages less."))

length contraction

The length of an object moving relative to an observer is measured to be shorter along its direction of motion than when it is at rest.

proper length

l0
the length of the object (or distance between two points whose positions are measured at the same time) as determined by OBSERVERS AT REST with respect to the object

length l

length measured by observers when the object travels past them at speed v

length attraction occurs...

only along the direction of motion

four-dimensional space-time

space takes up 3 dimensions and time is a 4th dimension

space-time interval

(∆s)^2 = (c∆t)^2 - (∆x)^2

relativistic momentum

the momentum of an object when measured in the frame of reference in which the object is in motion

for speeds much less than the speed of light, use (momentum)

p=mv

relativistic mass

The mass of a moving body as measured by an observer in the same frame of reference.

rest mass

m0
mass of an object when it is at rest relative to the observer

ultimate speed

speed of an object cannot equal or exceed the speed of light

rest energy

mc^2
The amount of energy that would be produced if all of a particle's mass was transformed into energy.

total energy E of the particle (assuming no PE)

γmc^2

for a particle at rest in a given reference frame...

KE is zero, so the total energy is its rest energy
(E=mc^2)

at low speeds, v<<c, the relativistic formula for kinetic energy...

reduces to the classical one

invariant energy-momentum

at any given moment the total energy E and momentum p of a particle will be different in different reference frames, but the quantity (E2-p2c2) will have the same value in all inertial reference frames (so it is invariant)

for speeds less than 0.10c or if expected precision is no better than 1%...

we can use the simpler classical formulas

relativistic addition of velocities

since length and time are different in different reference frames, the classical addition-of-velocities formula is no longer valid
*for motion along a straight line

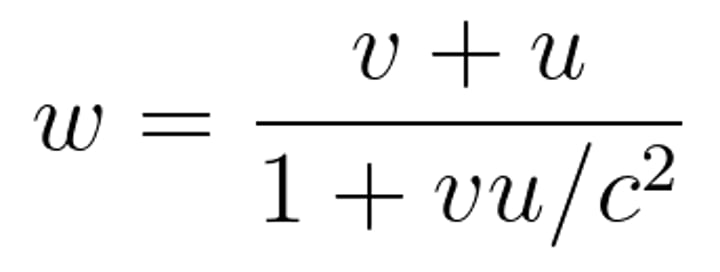
u'

speed with respect to the first rocket

u

speed of the rocket with respect to the Earth

if u' is in the opposite direction from v, then...

u' must have a minus sign, so

u = (v-u')/(1-vu'/c^2)

correspondence principle

insistence that a more general theory (such as relativity) give the same results as a more restricted theory (such as classical mechanics which works for v <<c)