AP Physics C Mechanics Equations to MEMORIZE

J = ∆p = F∆t

Impulse-Momentum Theorem

(impulse, J is measured in unit seconds)

W = ∆E

Work-Energy Theorem

vf² = vi²+2a(xf-xi)

vi² = vf²-2a(xf-xi)

Kinematic equation solving for Vf without t

Fg = mg

The Force of Gravity or Weight of an object

Δx = 1/2(vf +vi)Δt

The fourth Uniformly Accelerated Motion equation

Fg⊥ = mgcos θ & Fgll = mg sin θ

The components of the force of gravity parallel and perpendicular on an incline where θ is the incline angle

0 - 2

General range for coefficients of friction

ΔEsystem = ∑T

The general equation relating the change in energy of the system to the net energy transferred into or out of the system.

W = ∑ΔKE

Work energy theorem -always true.

Wfriction = ΔME

Nonconservative forces 1 -only true when there is no energy added to or removed from the system via a force.

MEi = MEf

Nonconservative forces 2 -only true when there is no energy added to or removed from the system via a force and there is no work done by a nonconservative force.

Fx =−dU/dx

The equation which relates a conservative force and the potential energy associated with that force -Force is the derivative of potential energy with respect to displacement

That every derivative is ____

That every derivative is an integral and every integral is a derivative.

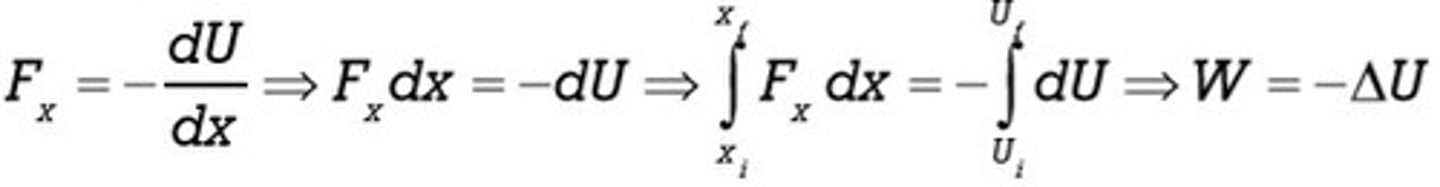
∑->Pi = ∑->Pf

Conservation of Momentum. It may seem obvious, however, you need to remember when it is valid.

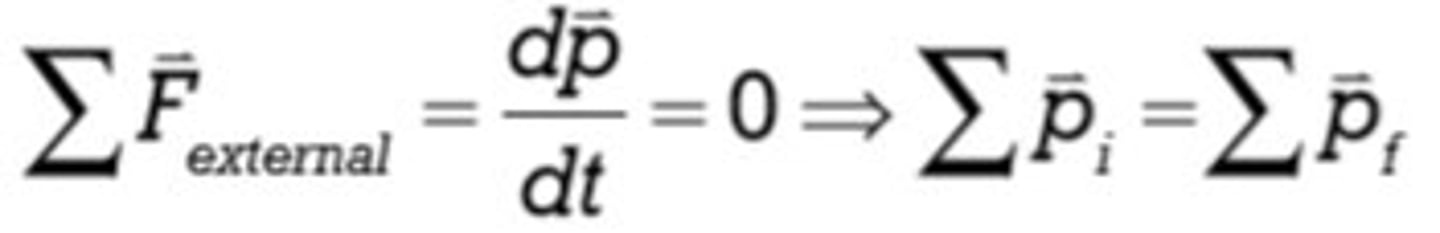
∑->Li = ∑->Lf

Conservation of Momentum. It may seem obvious, however, you need to remember when it is valid.

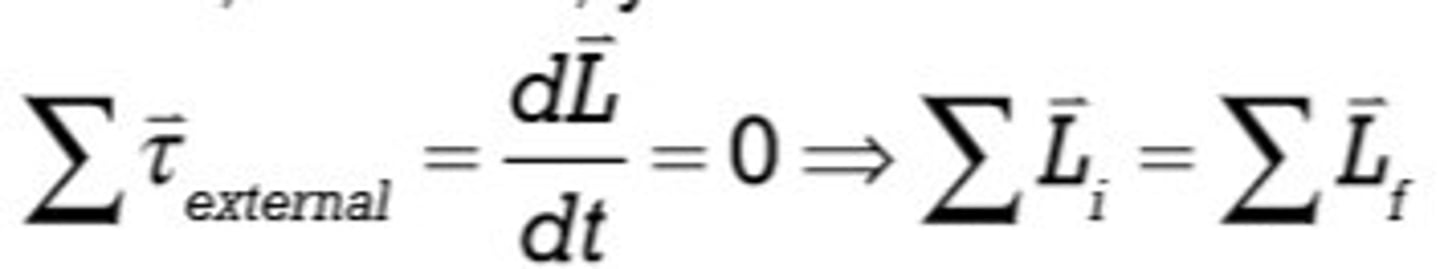
rcm = (1/mtotal)*∫*rdm

The center of mass of a rigid object with shape (do not confuse with moment of inertia I=∫r²dm)

ρ = m/∀ & λ = m/L

Volumetric Mass Density and Linear Mass Density

s = rΔ θ & at = r α

Arc length and tangential acceleration. vt = r ω is on the equation sheet, so it is easy to get to the other two.

Vcm = Rω & acm = R α

The velocity and acceleration of the center of mass of a rigid object which is rolling without slipping. Easy to remember from the previous equations.

360° = 2 π radians

1 revolution (conversion factor)

(ω f)² = (ω i)² + 2 α Δ θ & Δ θ = 1/2 (ω i + ω f) Δt

Uniformly Angularly Accelerated Motion equations

d²x/dt² = − ω²x

The condition for simple harmonic motion

vmax = A ω

The maximum velocity during simple harmonic motion

amax = A ω²

The maximum acceleration during simple harmonic motion

x(t) = Acos(wt+θ)

v(t) = -Awsin(wt+θ)

a(t) = -Aw²cos(wt+θ)

Displacement, Velocity, and Acceleration of Simple Harmonic Motion

->Fr =−b->v & ->Fr = 1/2 D ρ Av²

Don't memorize -Resistive force equations. The problem will specify to use ->Fr = 1/2 D ρ Av² and give you that equation OR tell you the drag force is "proportional to" the velocity, which means ->Fr = -b->v

746 watts = 1 hp

Don't Memorize -Conversion will be provided

G =6.67×10−11 N⋅m² kg²

Don't memorize -reference the "Table of Information" and the page of general math formulas on the AP Physics equation sheet

vcm = ∑(mivi)/∑(mi) & acm = ∑(miai)/∑(mi)

Don't memorize -know how to derive. velocity and acceleration of the center of mass of a system of particles. Simply take the derivative with respect to time once or twice of the position of the center of mass of a system of particles to get these equations.

????????????vterminal = √[(2mg)/(DρA)]

???????????Don't memorize -Terminal Velocity (p is density)

WFa = Gmomp/Rp

Don't Memorize -Binding Energy

Vescape = √[2GmEarth/REarth]

Don't memorize (on calculator) -Escape Velocity

?????MEtotal = −Gmomp/2r

??????Don't Memorize -Total Mechanical Energy of an *Orbital* Object (mp is mass of planet)

T² = [4π2/Gmp]r³

Don't Memorize -Kepler's Third Law of periods: Kepler's constant describes the relationship of a planets period to its radius.

v (t) = −A ω sin(ωt+φ)

Velocity in simple harmonic motion

a (t) = −A ω² cos(ωt+φ)

Acceleration in simple harmonic motion

I = Icm+mD²

The parallel axis theorem

Icm = mR²

Uniform Hoop or thin cylindrical shell about its cylindrical axis

Icm = 1/12 mL²

Moment of inertia [center of mass] for Uniform Thin and Long rod about center axis

Icm = 1/2mR²

Moment of inertia [center of mass] for Uniform Solid cylinder or disk about its cylindrical axis & Moment of inertia for a Hoop around its diameter (not symmetric)