MATH 2413 Limits Concepts and Approaches

This goes over some important to remember concepts as well as approaches to solving problems

Which type of line touches a curve at only ONE point?

Tangent Line

Which type of line touches a curve at TWO points?

Secant Line

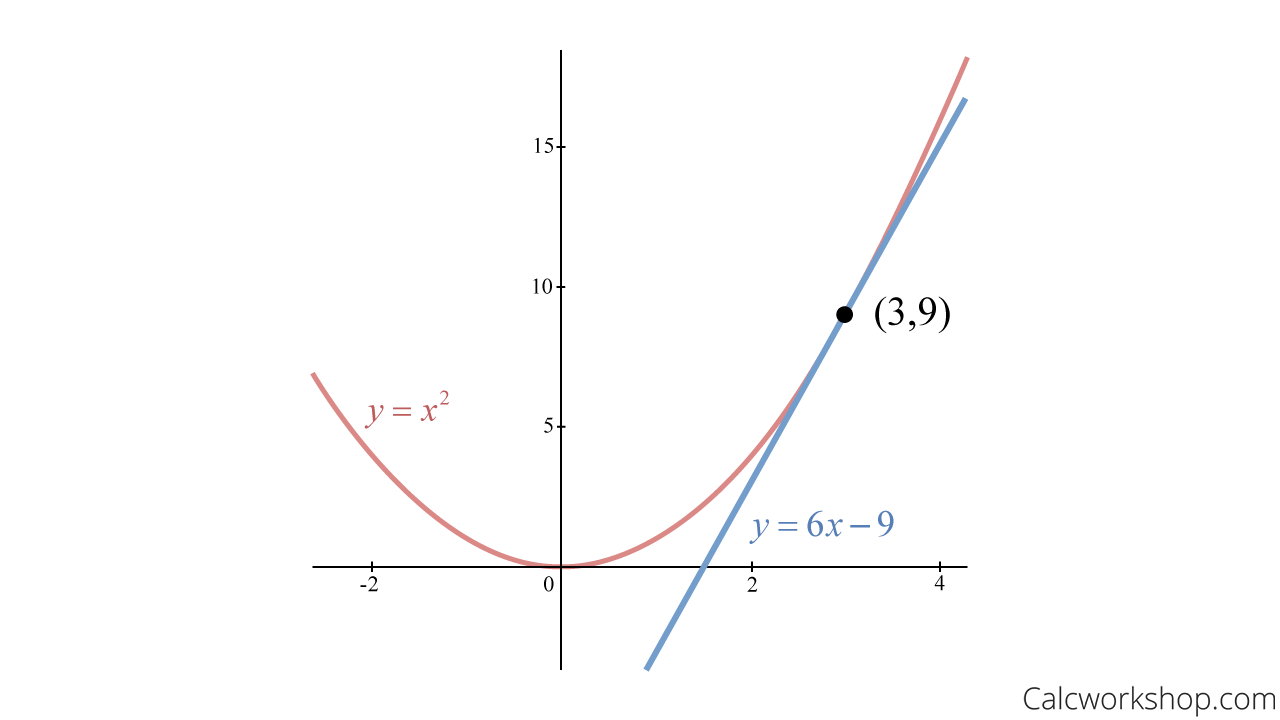
Which type of line is displayed?

Tangent Line

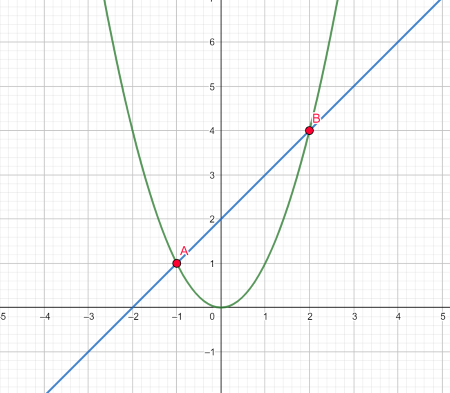
Which type of line is displayed?

Secant Line

Which direction is the limit of a function approaching from, if the values of it’s one sided limit, start less than the limit and get closer?

Approaching from the left

Which direction is the limit of a function approaching from, if the values of it’s one sided limit, start greater than the limit and get closer?

Approaching from the right

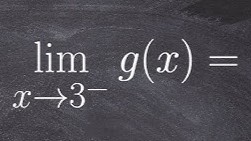
What does this notation read?

The limit of g of x as x approaches 3 from the left.

What is the formula for definition of a derivative?

f(x+h) - f(x)/h

What is infinity over infinity equal to?

An indeterminate form.

What is 0 over 0 equal to?

An indeterminate form.

What is infinity over a constant equal to?

Infinity, with respect to the sign of the fraction.

What is a constant over infinity equal to?

0, as the denominator approaches infinity, the value of the fraction gets smaller, approaching zero.

What are some algebraic ways to simplify a limit equation if you can’t take the limit directly (or in other words plug in)?

Factor, rationalize, distribute.

How can you find when a function is not moving or constant?

By finding the derivative, and making the equation of the derivative equal to zero.

How can you find when if a function is increasing or decreasing at a certain point.

Evaluate the derivative at that point, if the number is positive or > 0 the original function is increasing, if the number is negative or < 0 the original function is decreasing.

What has to be true about a functions one sided limits, in order for its limit to exist?

They must be equal.

When can you cancel out values within a fraction.

When everything is multiplying and dividing.

What is a the square root of a variable squared. Example: square root of x²

The absolute value of the variable, denoted as |x|.

When given a nice enough values, what is the easiest way to solve for a limit?

By taking the limit.

How can you determine where a function is NOT continuous?

By taking it’s denominator and setting it equal to 0.

What three things must be true in order for function to be continuous?

The function must be defined at the point, the limit from the left must equal the limit from the right, and both must equal the function's value at that point.

How are derivative functions denoted.

f’(x) ( f prime of x).

What is a limit essentially?

What a function approaches as the x value gets closers to a specific point.

When should you stop including the limit notation when solving for a limit?

Whenever you take the limit.

Any number divided by 0 is?

Undefined (it will make the world explode).

In order to remove a root function from the numerator you must do what?

Multiply the numerator and denominator by the conjugate.

(√5+x + √5+x) can be rewritten as?

2√5+x

A number to the negative power means what?

It means that the value is equal to 1 over, what the value would be equal to if it was raised to a positive power, for example. 2^-3 = 1/8.

What is the easiest way to divide fractions?

Multiply the numerator by denominator of the reciprocal (Keep Change Flip). (Just remember that dividing by two is the same as multiplying by 1/2.

If a function gives us position, what will finding the derivative of that function tell us?

The velocity.

When evaluating limits at infinity, it is a good idea to do what?

Factor out the term with the highest exponent.

When evaluating infinite limits what is a good approach?

Plug values in as your x value gets closer to it’s limit.

e raised to infinity is equal to?

Infinity

e raised to negative infinity is equal to?

0

What is the difference between limits at infinity vs infinite limits.

Limits at infinity have an x value that approaches infinity or negative infinity (infinity, negative infinity, or 0). Infinite limits have a limit that is equal to infinity or negative infinity, while their x approaches a constant.