Math 152 Exam 2

csc²x=

cot²x+1

cot²x=

csc²x-1

cos(2x)= (cos)

2cos²x-1

cos2x= (sin)

1-2sin²x

cos²x= (power reducing identity)

½ (1+cos(2x))

sin²x= (power reducing identity)

½ (1-cos(2x))

d/dx csc(x)

-csc(x)cot(x)

d/dx cot(x)

-csc²(x)

sec(x)

1/cos(x)

csc(x)

1/sin(x)

cot(x)

1/tan(x)

sin(2x)

2sin(x)cos(x)

∫sec(x)dx

ln |sec(x)+tan(x)| + C

∫sec³(x)dx

½ (sec(x)tan(x) + ln |sec(x) +tan(x)|) + C

√a²-x²

asin(x)

√x²+a²

atan(x)

√x²-a²

asec(x)

∫1/(x²+a²)dx

(1/a)(arctan(x/a)) + C

∫1/(x√x²+a²)dx

(1/a)(arcsec(x/a) + C

∫1/(√a²-x²) dx

arcsin(x/a) + C

What is an improper fraction?

A fraction where the numerator is greater than the denominator

What is an improper integral?

• An integral over which you are integrating is infinite (one of the bounds is ±∞

or

• the function has a discontinuity somewhere in the integral over which you are integrating

When does an integral converge?

the limit exists

When does an integral diverge?

If the limit does not exist

When does ∫₁^∞(1/x^p)dx converge?

p>1

When does ∫₁^∞(1/x^p)dx diverge?

p<=1

When comparing two functions, when does ∫(a-∞)f(x)dx converge?

f(x)<=g(x), ∫g(x)dx converges

When comparing two functions, when does ∫(a-∞)f(x)dx diverge?

f(x)>=g(x), ∫g(x)dx diverges

What is a sequence?

an ordered list of numbers

What is a number in a sequence?

a term

What is an alternating series?

a sequence where the terms alternate signs

When does an alternating series converge?

• lim→∞(b_n) = 0

What is a monotonic sequence?

a sequence that is either increasing or decreasing

What monotonic series converge?

Ones that are bounded

What do you need to do when you are testing if a series converges?

Remember to state you are comparing it to the limit of a function, you cannot take the derivative of a sequence

What is a recursive sequence?

A sequence where terms are defined by using previous terms in the sequence, you have to be given the 1st term

What is a series?

The sum of an infinite sequence of numbers. They sometimes have and sometimes don’t have a finite sum

Where does a series converge?

The series converges to its limit

How do you know if a series converges?

• its limit approaches 0

• AND converges by the tests we have

  • s_n has a limit

  • evaluating telescoping series

  • evaluating geometric series

Do harmonic series converge?

the terms go to zero but do not converge

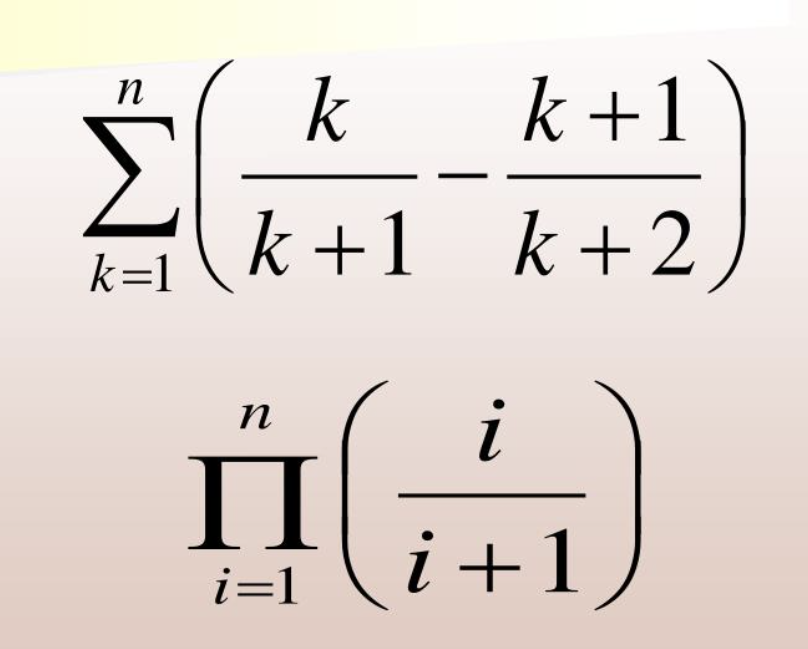
What is a telescoping series?

Series where all but a finite number of terms of the series cancel out with other terms

What is one way that you can organize a series to be a telescoping series?

partial fractions

What is a geometric series?

A series where each term of the series is some ratio r to the previous term where r is some real number

What is a sequence of partial sums?

a sequence of sums of sets of terms of a sequence

What is the relationship between a sequence of partial sums converging and the behavior of that series it comes from?

The series also converges

What is the number an infinite sequence of partial sums converges to?

The sum of the series

When does a geometric series converge?

|r|<1

What is the sum of a geometric series?

s= a/(1-r)

What are the series we can find a sum for?

• we know s_n

• convergent telescoping series

• convergent geometric series

What is the integral test?

evaluate what an improper integral of f(x) converges to or diverges where a_n=f(x)

What must you state before doing the integral test?

f(x) is continuous, positive, and decreasing on [1,∞)

How do you know if a_n converges when doing the integral test?

It converges to a real number

Is the number the integral test converges to what a_n converges to?

no