Section 4.2: 3 Special Conditions

The set of all solutions (Ax=b) is called the?

solution set

The ____ of an mxn matrix A is the set of all solutions to the equation Ax=0

nullspace

Proof: Nul A is a subset of R^n because each vector must be an element of R^n. Now check the three properties for subspaces.

1) 0 is in Nul A because the ____ satisfies the system of equations.

zero vector

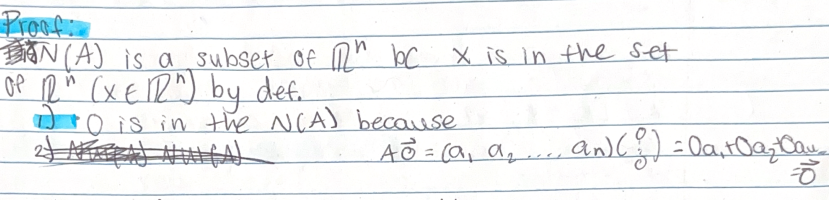
condition 2) Null A closed under addition

3) Null A is closed under scalar multiplication

the column space of an mxn matrix A with columns a1,a2,…,an is

Col A = Span {a_{1 ,}a₂ , …., a_n }

The ___ is the range of A

column space

the row space of an mxn matrix A with rows r₁, r₂, … , r_m is

Row A = span{r₁, r₂, … , r_m}

The row space is the ___ of A^T . So, the row space is a subspace of R^n

column space

subspaces of vector spaces other than R^n are often described in terms of a ____ instead of a ____

linear transformation, matrix

A ____ T from a vector space V into a vector space W is a rule that assigns each vector x inside of V to a unique vector function T(x) inside of W such that for all u,v in V and scalars c, T(u+v) =? and T(cu) =?

T(u+v) = T(u) + T(v), T(cu) = cT(u)

The kernel is the same thing as the __

null space

The kernel (or null space) of a linear transformation T is the set of all u in V such that…

T(u) = 0

The ___ of T is the set of all vectors T(x) for some x in V

range

The Kernel and nullspace the range of a linear transformation correspond to the ___ and the ____ of a matrix

null space, column space

T/F: The null space of A is the solution set of the equation Ax = 0

T

T/F: A null space is a vector space

T

The null space of an m x n matrix is in R^m

false, the null space is in R^n

The column space of an mxn matrix is in R^m

T

The column space of A is the range of the mapping x—> Ax

T

T/F: Col A is the set of all solutions of Ax=b

F

T/F: if the equation Ax=b is consistent, then Col A = R^m

F

T/F: Nul A is the kernel of the mapping x —> Ax

T

T/F: the kernel of a linear transformation is a vector space

T

T/F: Col A is the set of all vector that can be written as Ax for some x

T

T/F: the set of all solutions of a homogenous linear differential equation is the kernel of a linear transformation

T

T/F: The row space of A is the same as the column space of A^T

F

T/F: the null space of A is the same as the row space of A^T

F