R2: Hele pensum

Hva er derivasjonsregelen for eksponentielle funksjoner a^x?

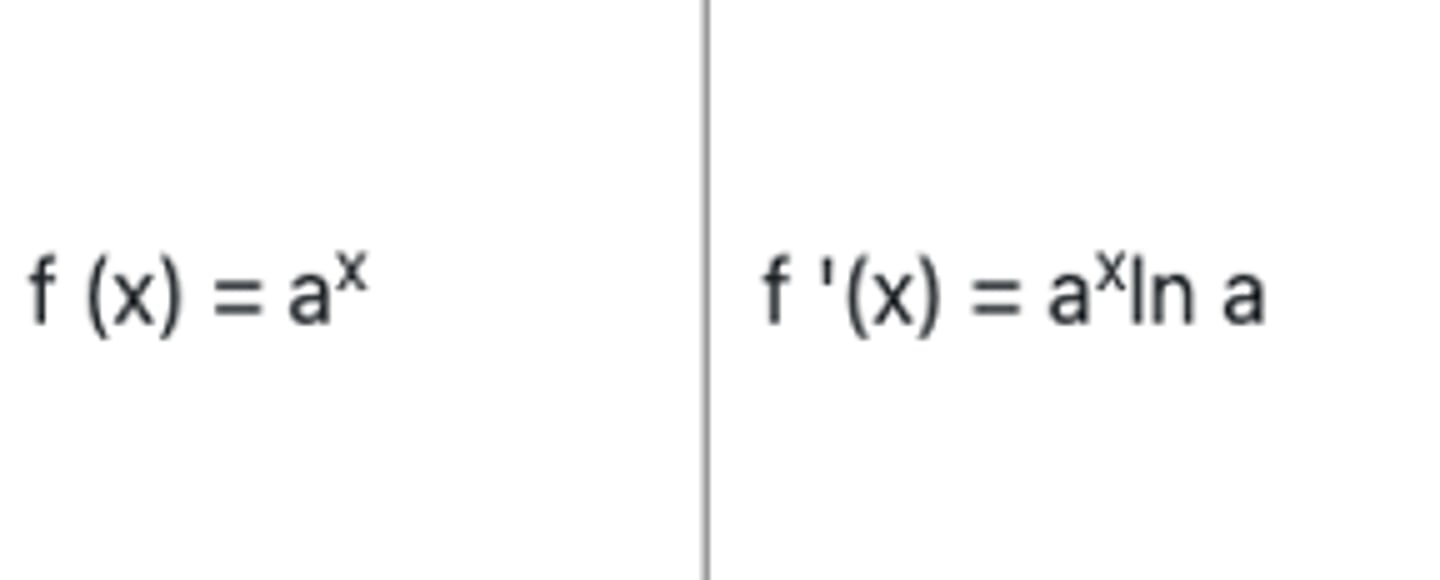
Hva er derivasjonsreglen for e^x?

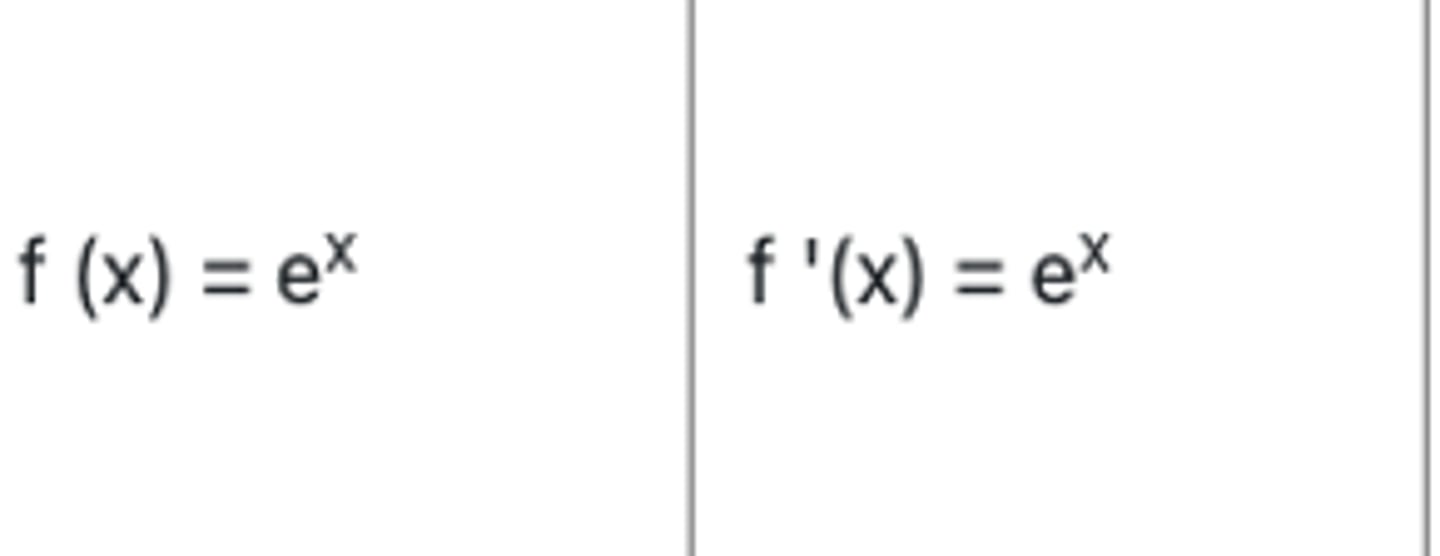
Hva er derivasjonsregelen for logaritmer?

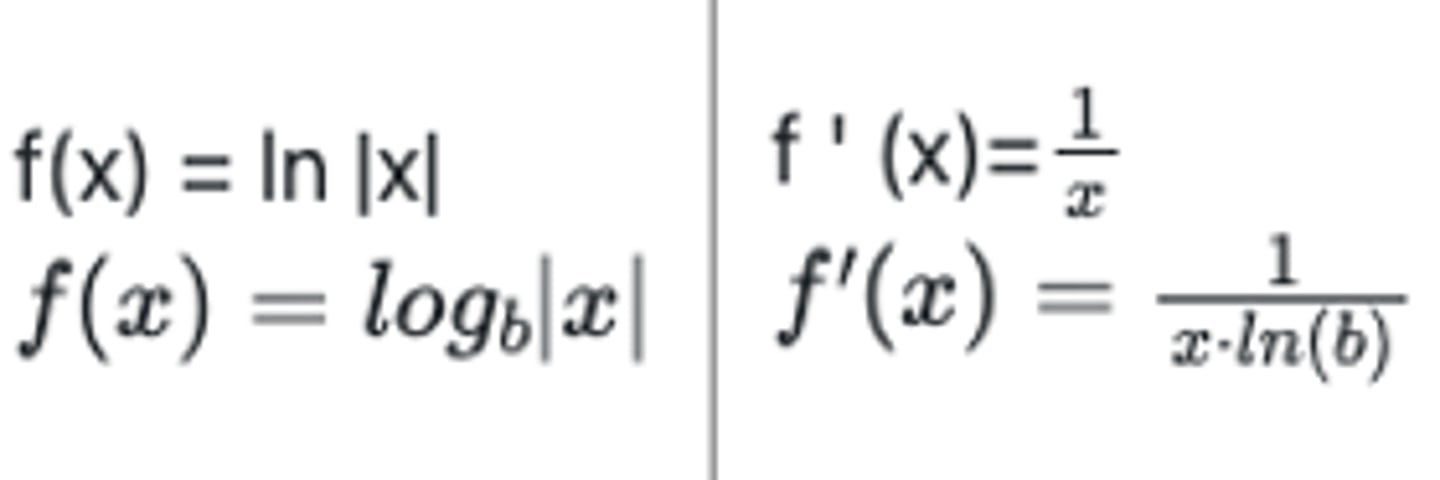
Produktregelen?

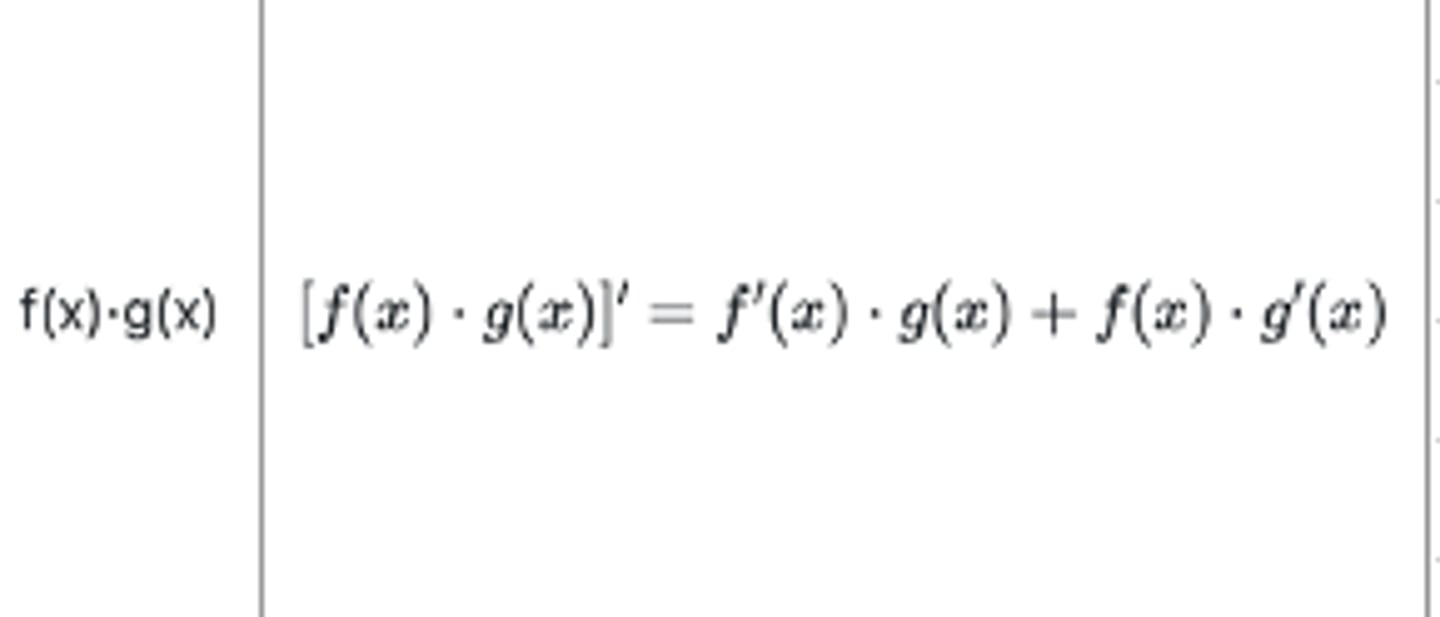
Kvotientregelen?

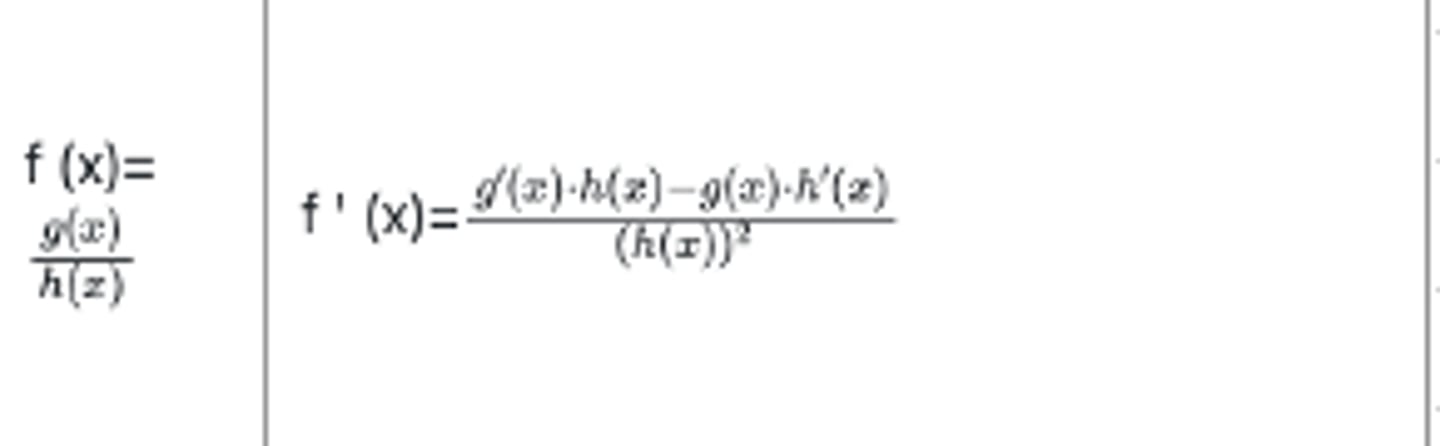
Kjerneregelen?

farten er den X av akselerasjonen

antideriverte

Akselerasjonen er X av farten

Den deriverte

Hva er forskjellen på en tallfølge og en tallmengde?

I en tallfølger har rekkefølgen noe å si

Hva kalles tallene i en tallfølger?

ledd

Hva slags formel har vi hvis vi har "en formmel for ledd nr. n"?

En eksplisitt formel

Hva er en rekursiv formel?

en formel for en tallfølger der vi ikke kjenner formelen for leddene men vi vet hva det første leddet er og sammenhengen mellom et ledd og leddet foran

Hva kjennetegner en aritmetisk følger?

Det er en fast differanse d mellom to ledd som følger etter hverandre

I en aritmetisk følger med differansen d er det første leddet lik a1, ledd nr. n er da gitt ved formelen ...?

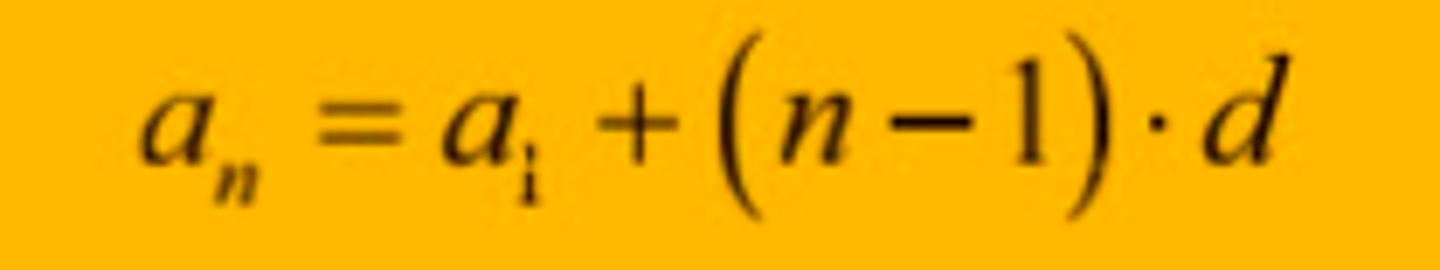
Summen av de n første leddene i en aritmetisk rekke er gitt ved formelen ... ?

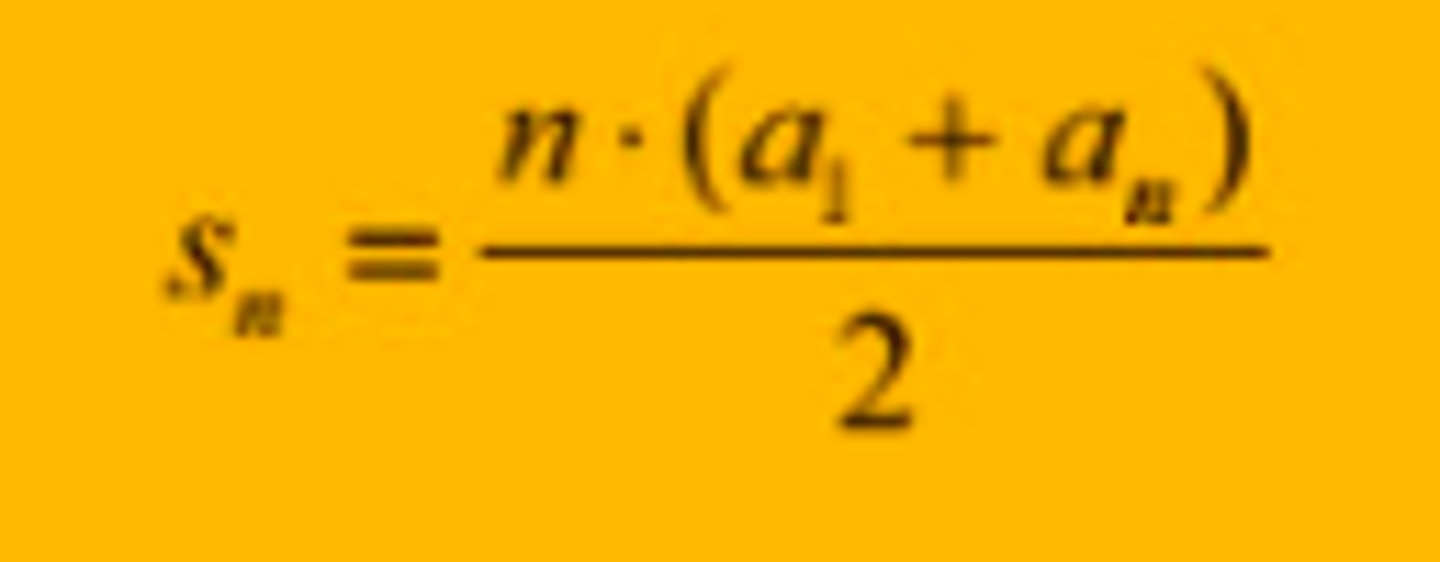
Hva får vi når vi summerer leddene i en aritmetisk følge?

en aritmetisk rekke

Hva er kjennetegnet til en geometrisk følge?

Det finnes alltid en kvotient, k, et tall, som vi kan gange med får å få neste ledd

en tallfølge er geometrisk med kvotienten k dersom ...

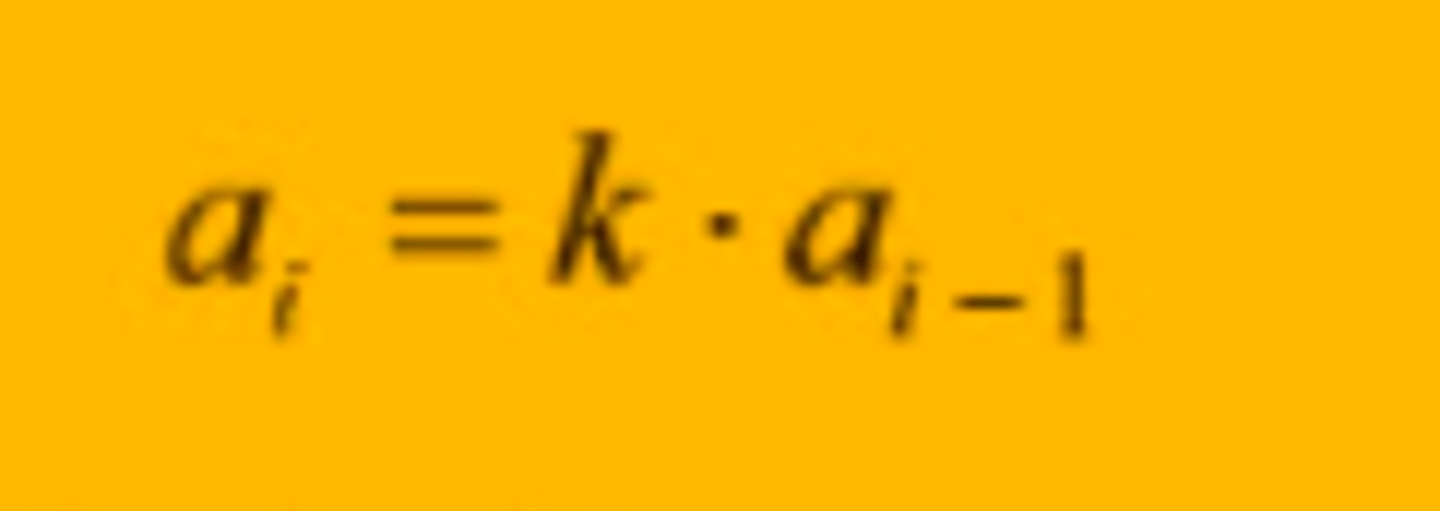
Hva er formelen for summen av de n første leddene i en geometrisk rekke dersom k ikke er lik 1?

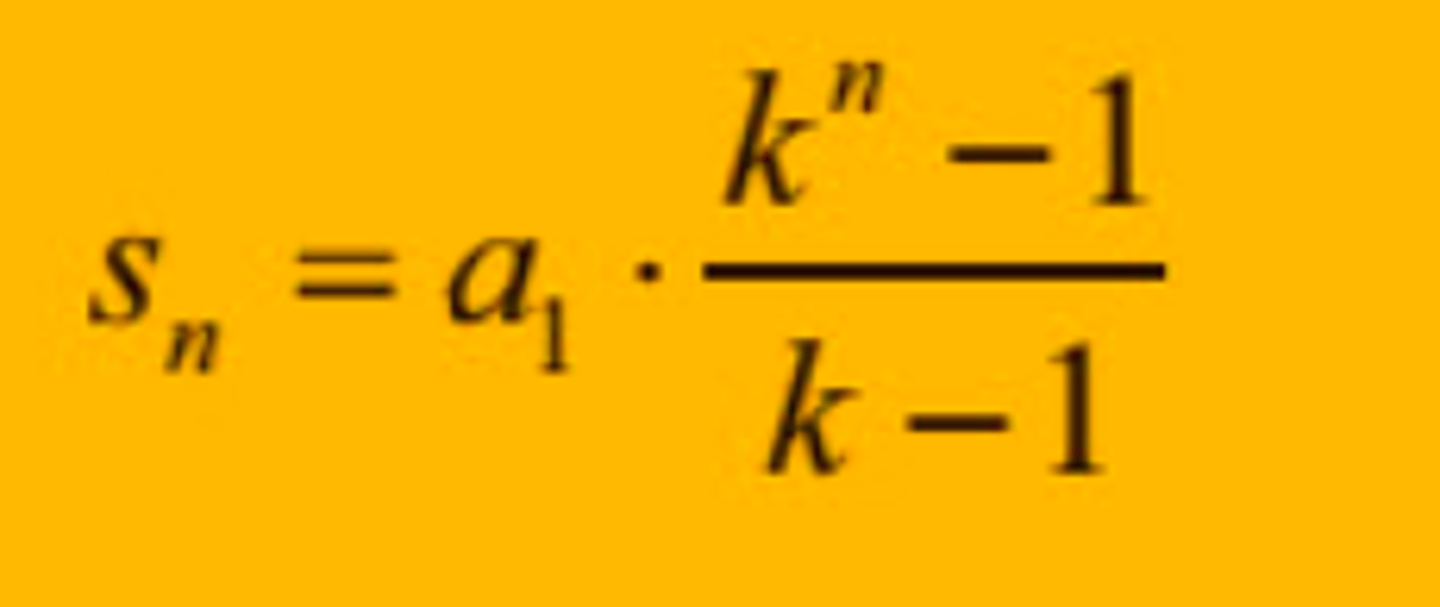
Hva er formelen for summen av de n første leddene i en geometrisk rekke dersom k = 1?

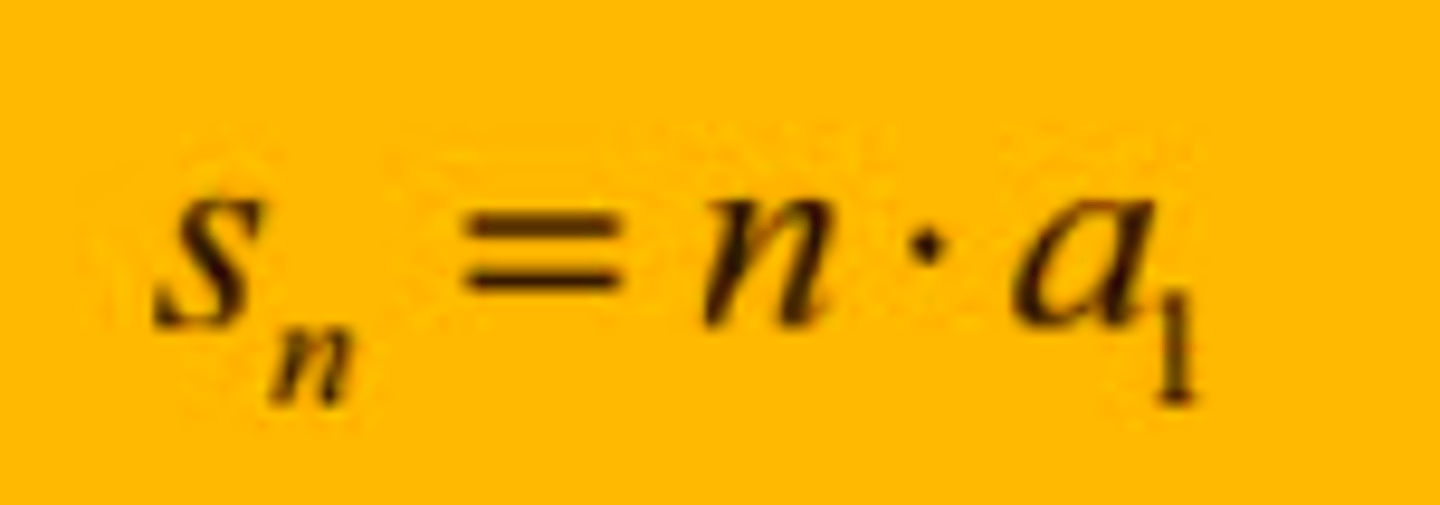
Hva vil det si at en uendelig geometrisk rekke er konvergent?

Når en uendelig rekke nærmer seg en bestemt sum når n går mot uendelig

Hva vil det si at en uendelig rekke er divergent?

når en uendelig rekke IKKE nærmer seg en bestemt sum når n går mot uendelig

en uendelig rekke med første ledd IKKE = 0 er konvergent hvis k = ...? Hva er formelen for summen av rekka da?

et sted mellom -1 og 1. Se bilde for summen.

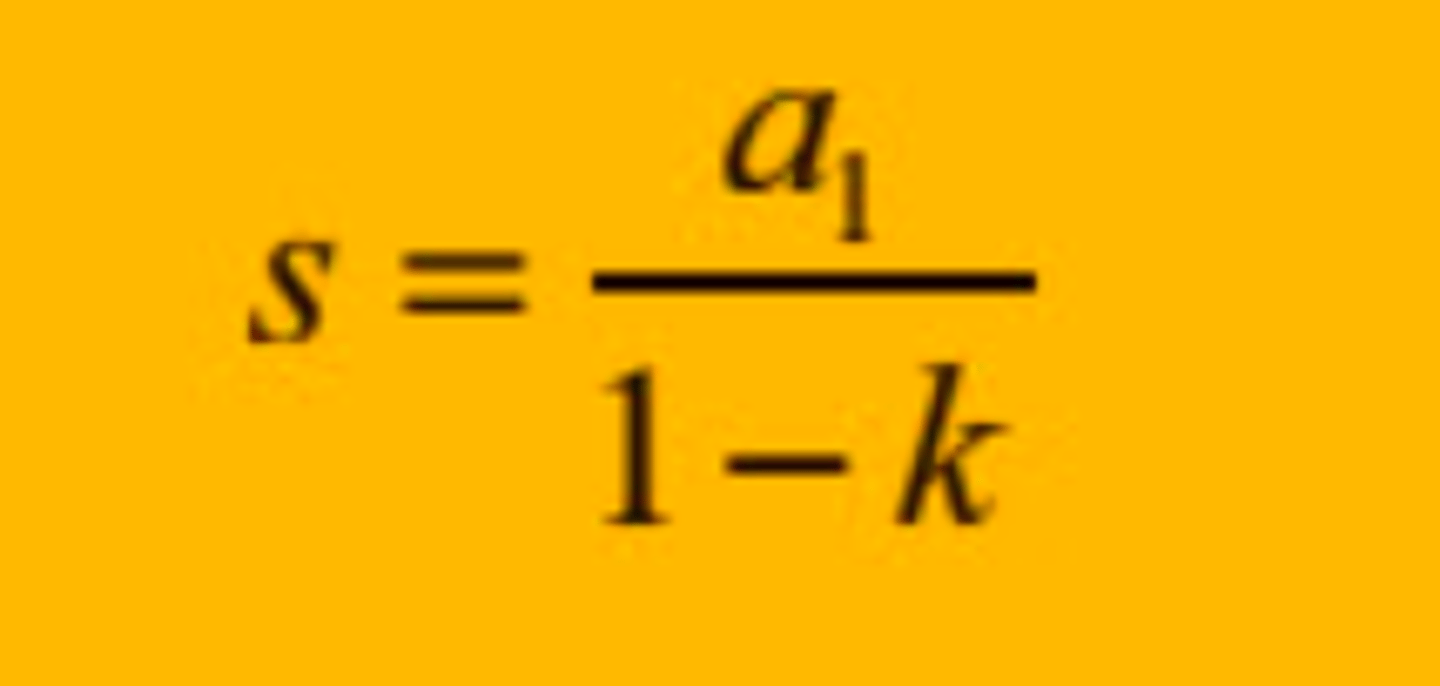
Hvordan beviser vi en påstand ved hjelp av induksjonsbevis?

1. Påstanden må være riktig for n=1

2. Hvis den er riktig for n=k må den og være riktig for n=k+1

formelen eller påstanden er da riktig for alle naturlige tall n

Formelen for omregning mellom grader og radianer

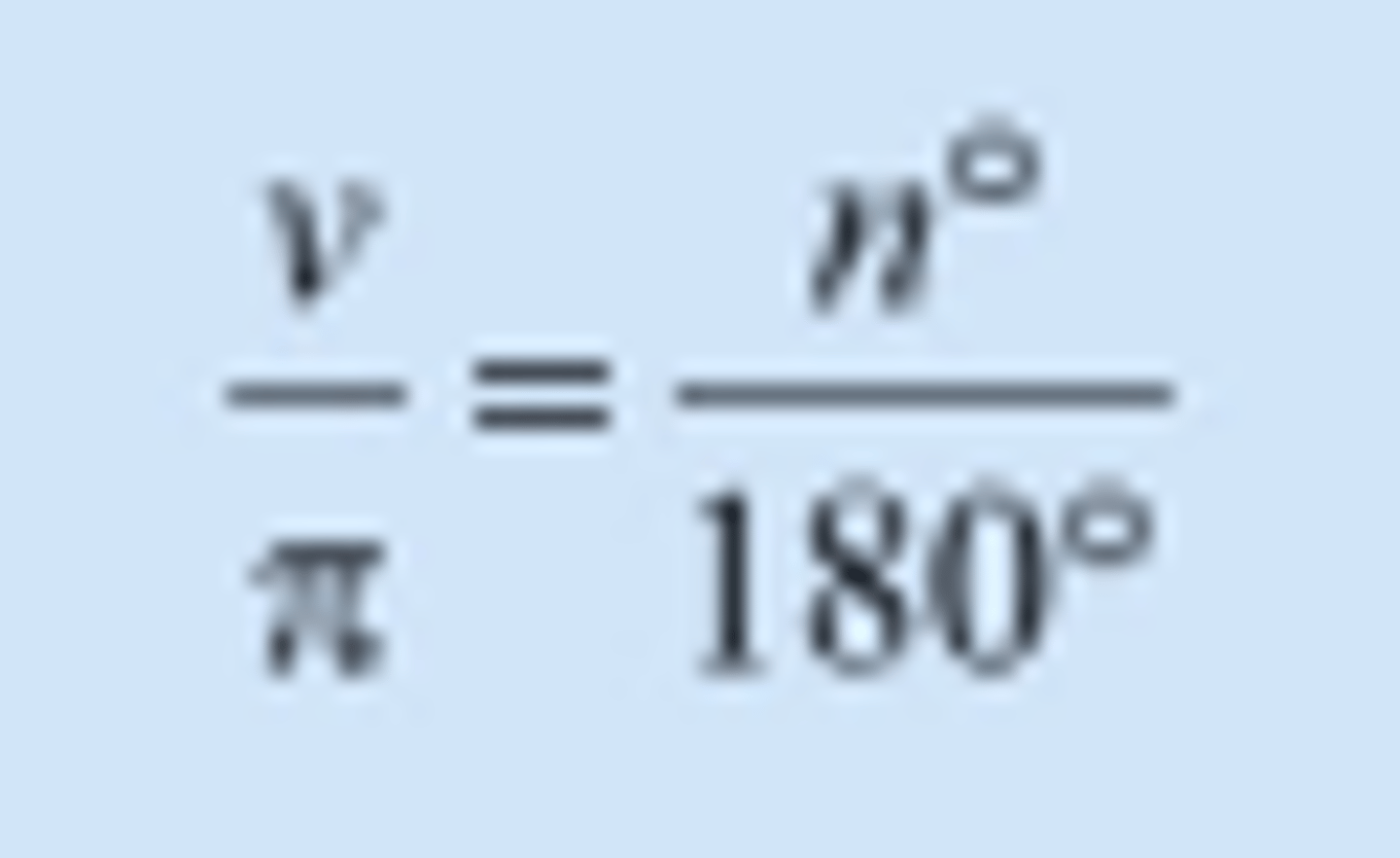
Enhetsformelen

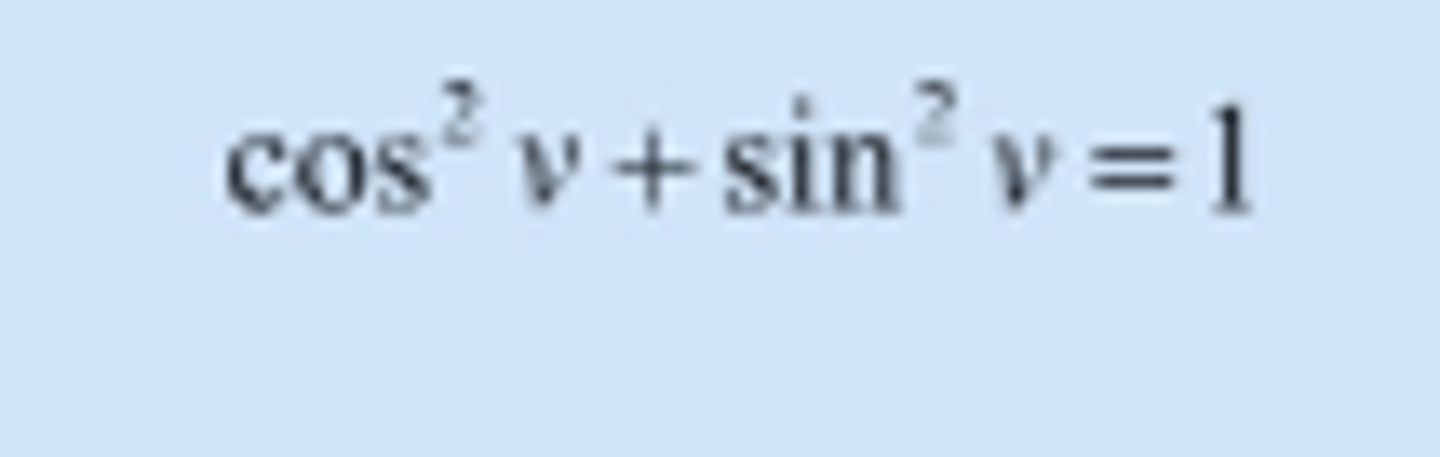
Hvordan finner man perioden til en sinusfunksjon?

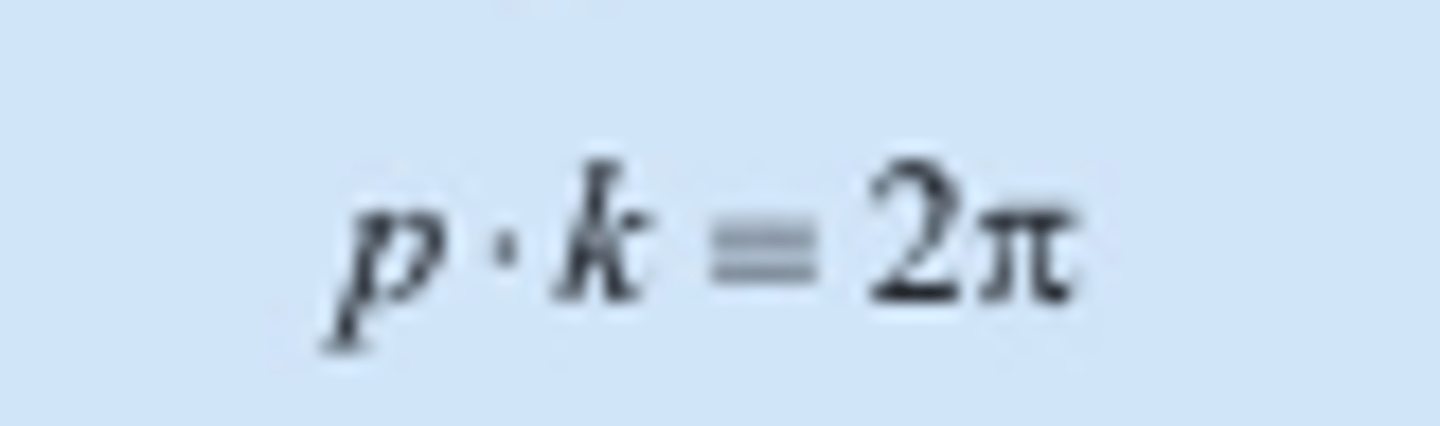
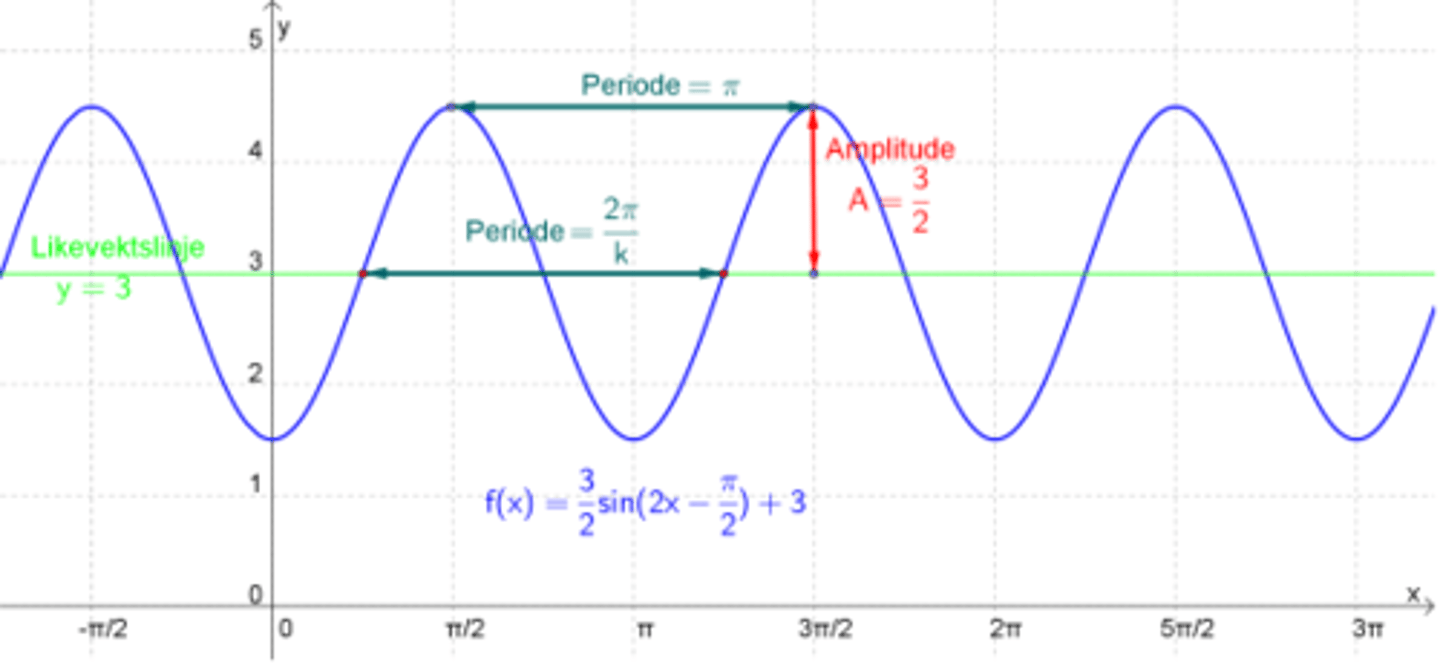
Hva er "oppsette" til grafen til en sinusfunksjon?

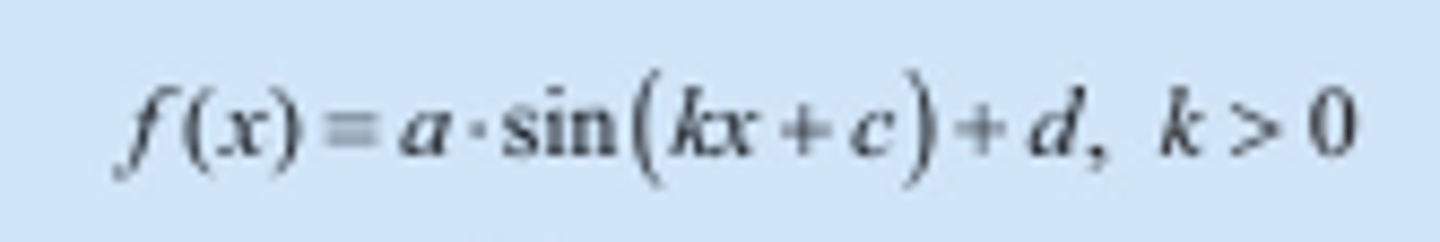
Hvrodan finner vi hvor grafen til sinusfunksjonen skjærer med likevektslinja?

Hva er periode, likevektslinje og amplitude?

Hva er "oppsette" til grafen til en cosinusfunksjon?

Hva er (sin x)'

cos x

Hva er (cos x)'

-sin x

Hva er (tan x)'

cos(-v)

cos v

sin(-v)

sin v

sin(u-v)

sin u cos v - cos u sin v

sin(u+v)

sin u cos v + cos u sin v

cos (u-v)

cos u cos v + sin u sin v

cos (u+v)

cos u cos v - sinusin v

sin(2v)

2sin v * cos v

cos(2v)

2cos^2x -1

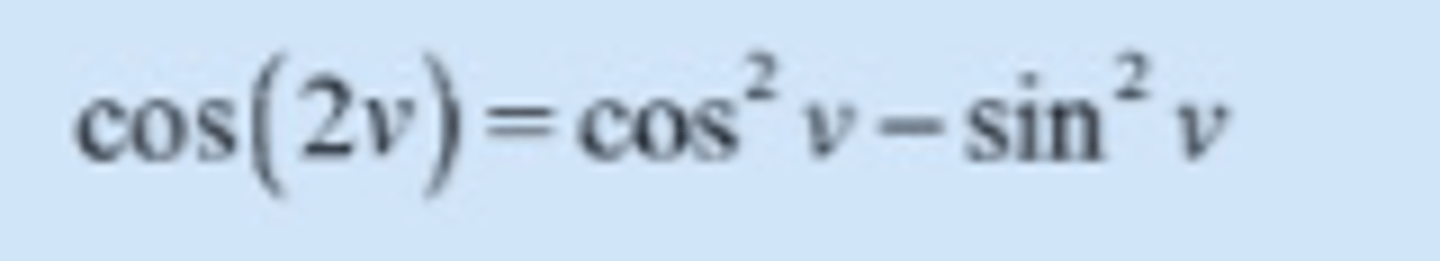
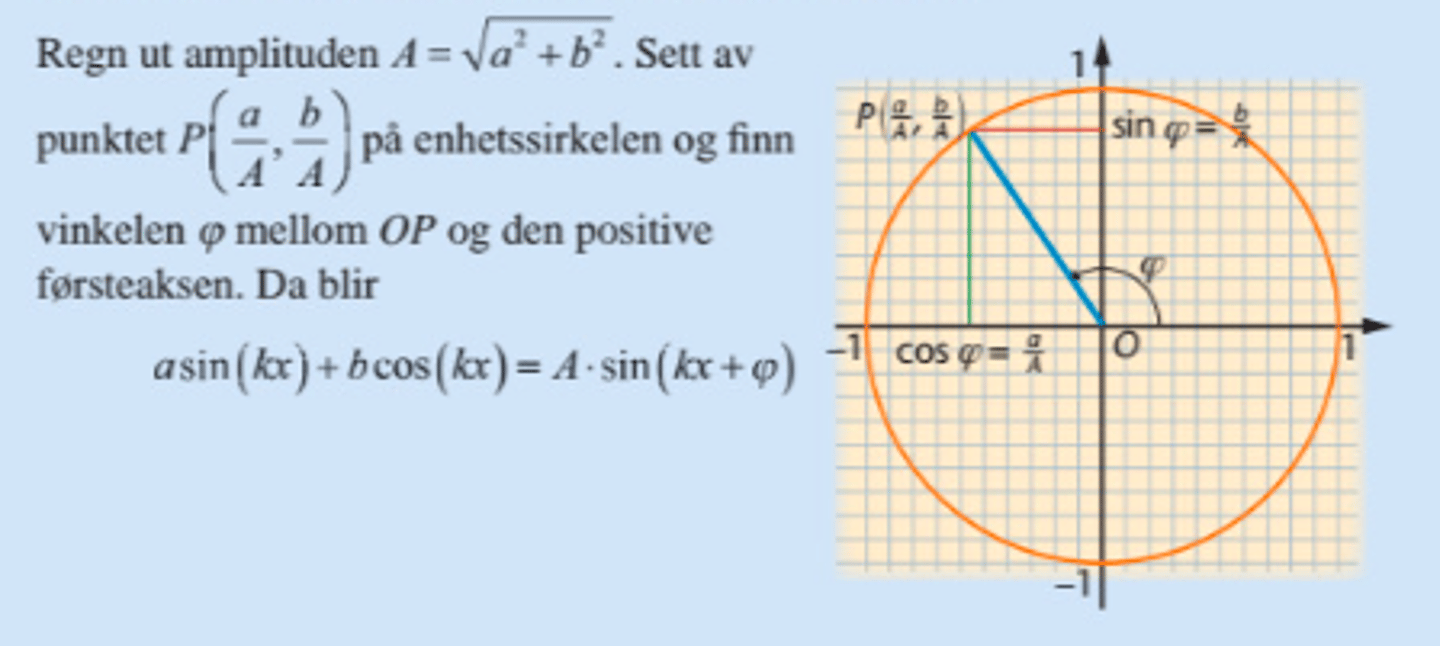
Hvordan skriver man om: a sin(kx) + b cos(kx) til et sinusuttrykk

Skalarprodukt

Hvordan regnes en 3x3 determinant?

Hvordan regner man vektorproduktet til to vektorer?

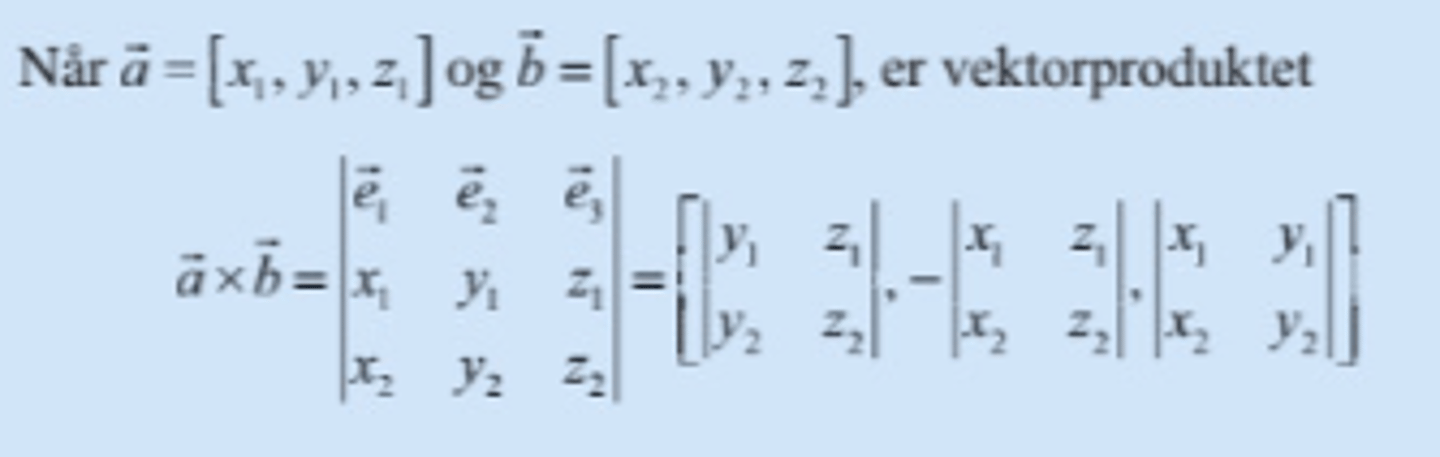
Hvordan finner vi arealet av et parallellogram ved hjelp av to vektorer?

Hvordan finner vi arealet av en trekant bestemt av to vektorer?

Hva er formelen for volumet ava en parallellepiped?

Hva er formelen for volumet av en pyramide med et parallellogram som grunnflate?

Hva er formelen for volumet av et tetraeder?

Hva er kravet for normalvektoren til et plan?

Hva er likningen til et plan i rommet?

Parameterframstilling for en rett linje

Hva er formelen for å beregne avstanden h fra et punkt P til linja L gjennom A med retningsvektor r?

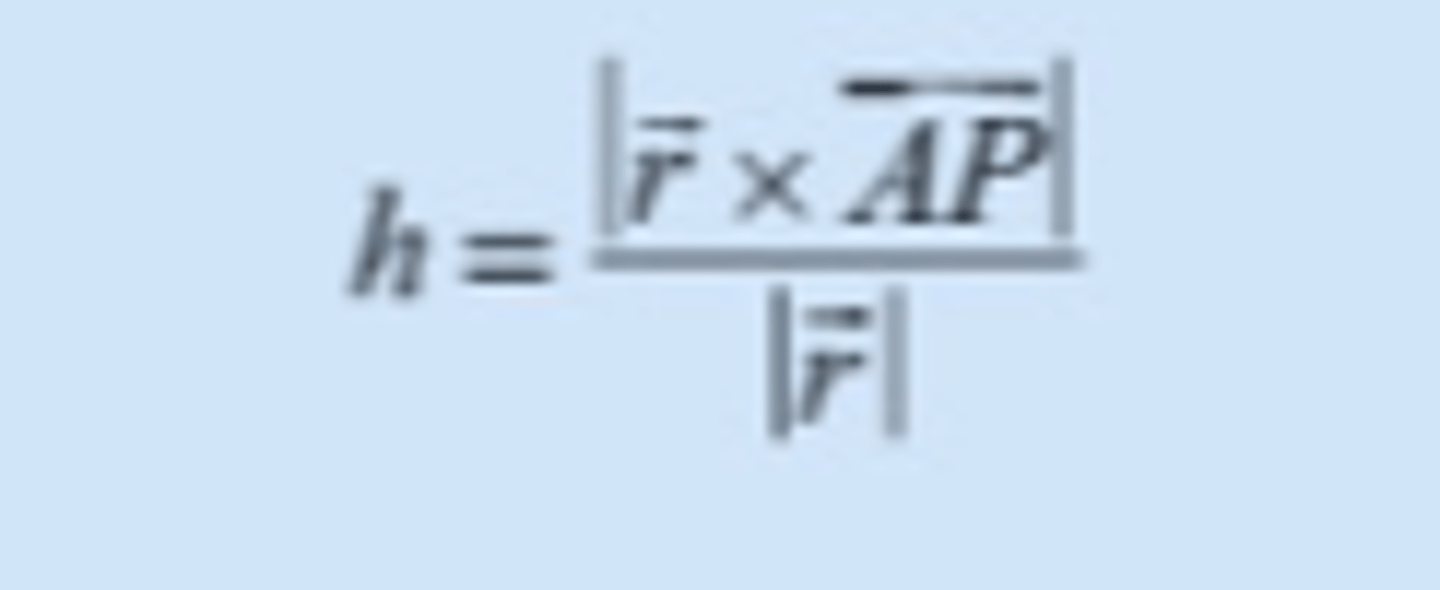
Hva er formelen for å beregne avstanden h fra punktet P(x, y, z) til planet alfa med likningen ax + by + cz + d = 0

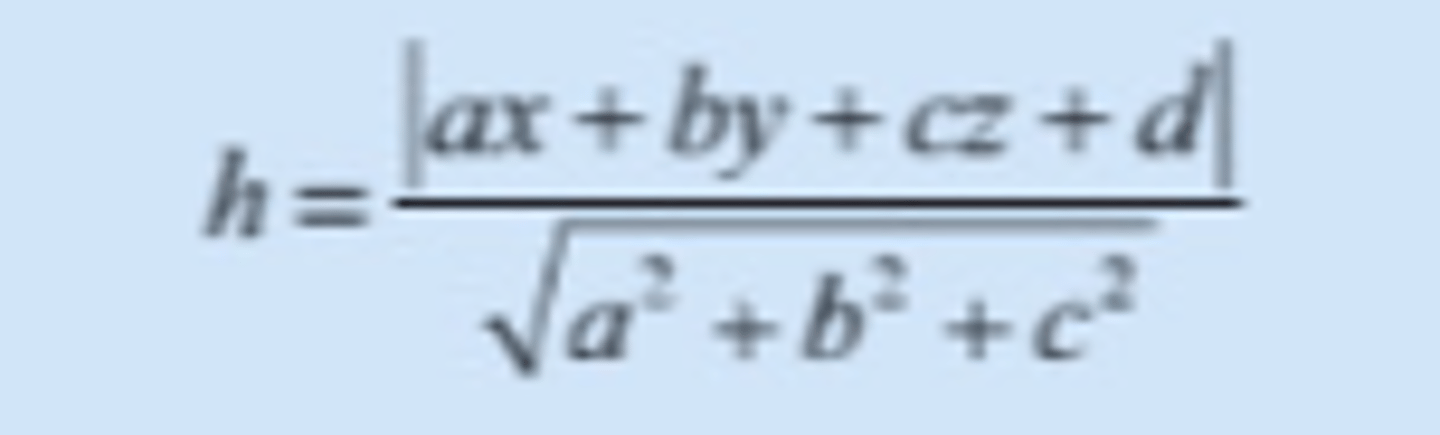
Hva er likningen for en kule?

Hva er parameterframstilling for et plan?

Hva er volumet av en omdreiningsgjenstand?

Integrasjon ved variabelskifte

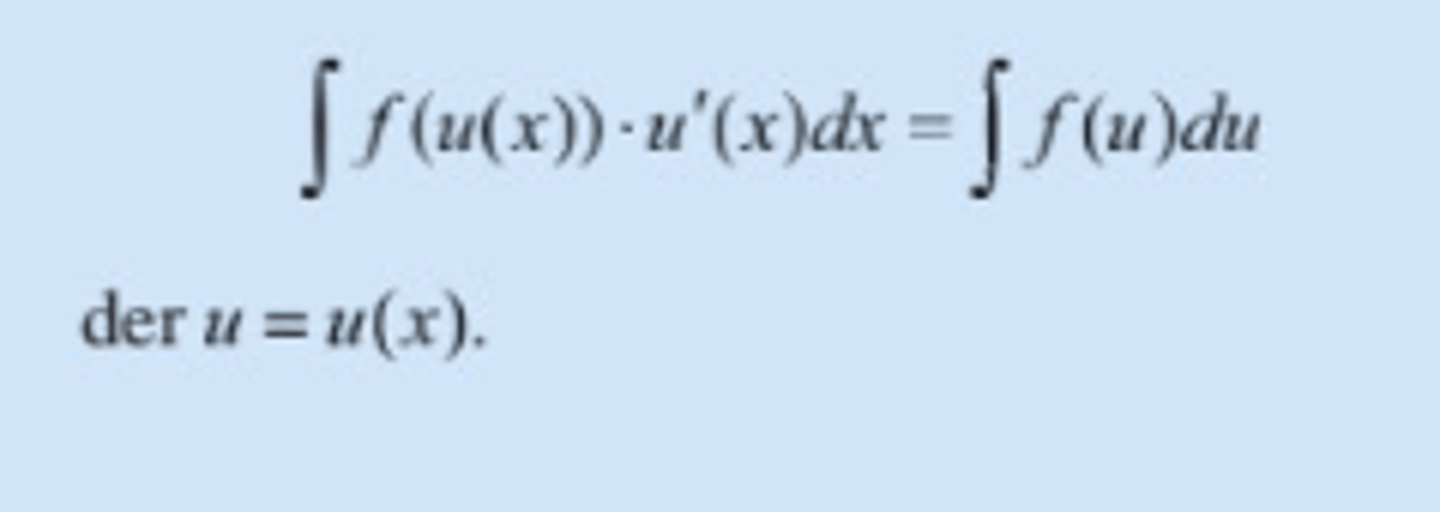
Delvis integrasjon

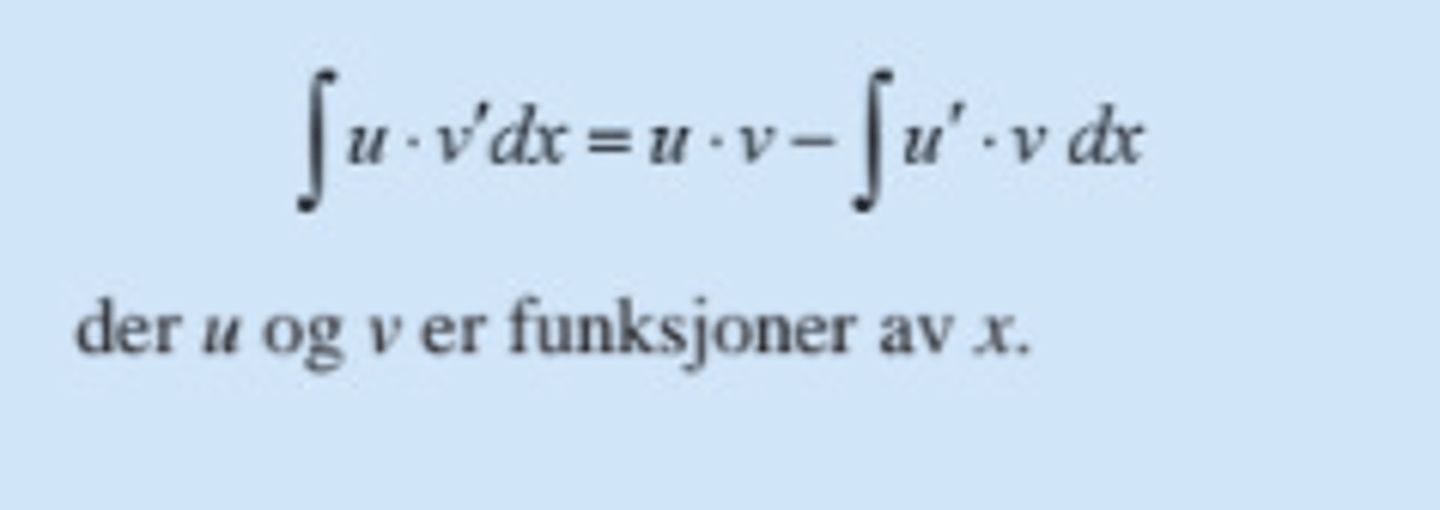
Hva er en differensiallikning?

Det er ukjent funksjon y = f(x) vi ønsker å finne. Likningen uttrykker en sammenheng mellom for eksempel y, y' og y'' som skal gi oss funksjonen

førsteordens differensiallikning

y'

lineær førsteorden differensiallikning

dersom g(x) = 0 er likningen homogen. Løses elsker deg <3 å multiplisere med den integrerende faktoren e^F(x) der F er en antiderivert til f

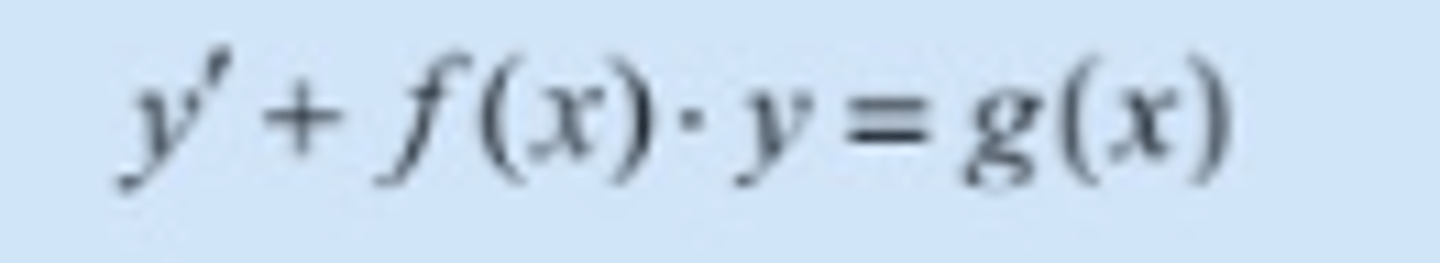
Seperabel differensiallikning

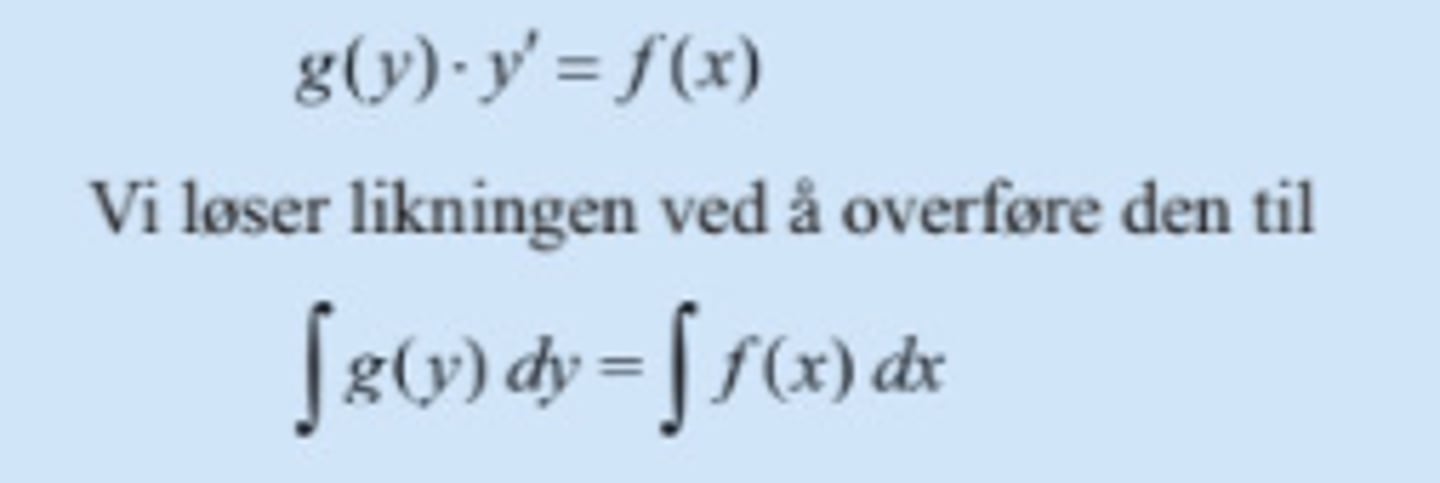
Andreordens differensiallikning

y'' kan skrives på formen på bilde

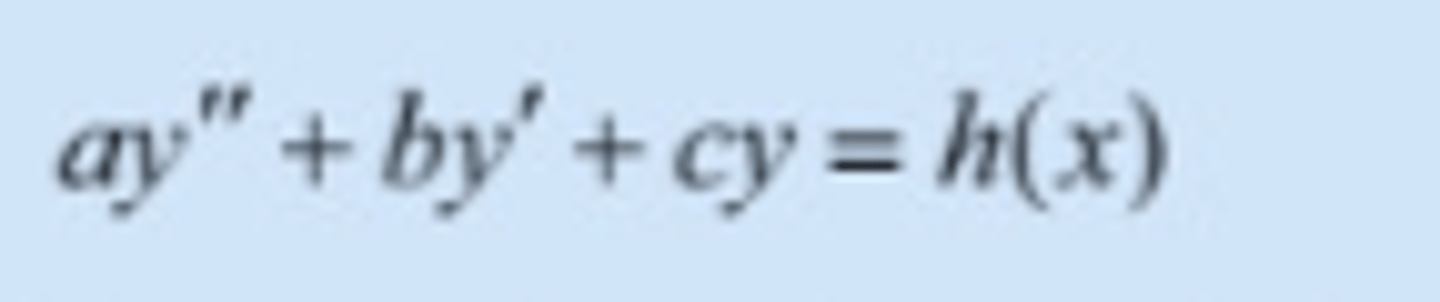
Andreordens Diff. likning: Karakteristiske løsningen har TO løsninger

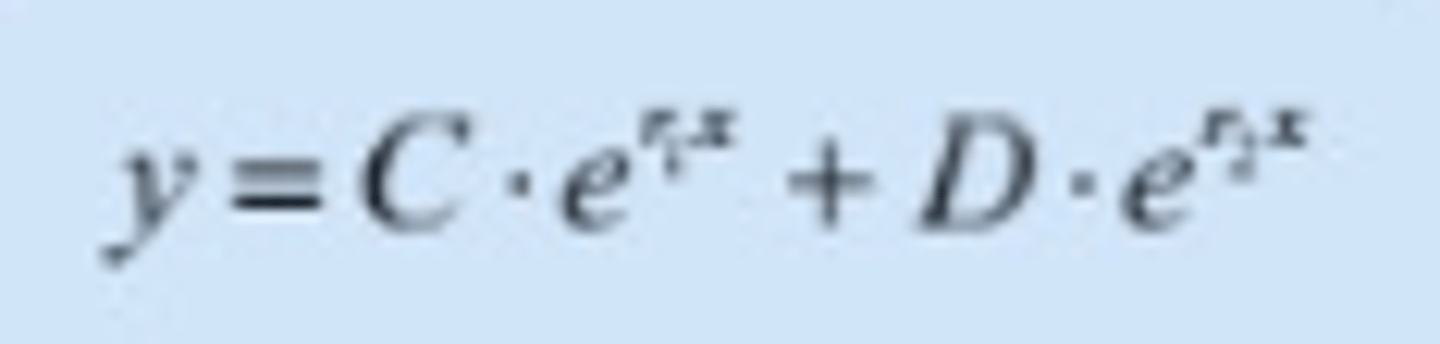
Andreordens Diff. likning: Karakteristiske løsningen har ÉN løsning

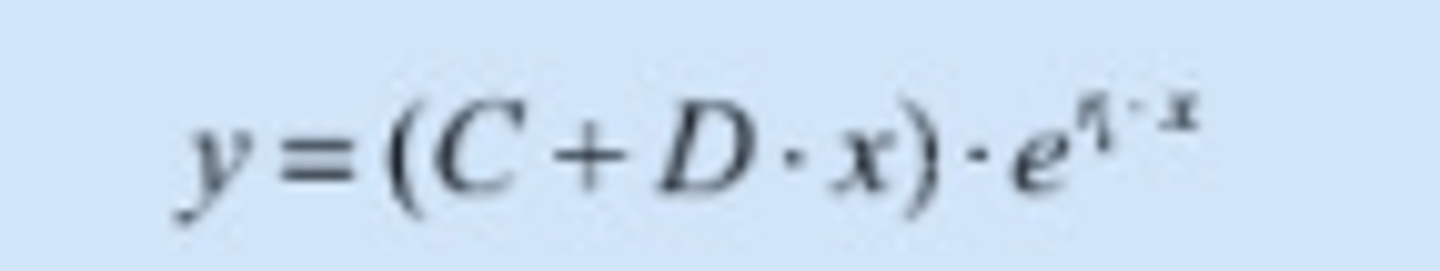
Andreordens Diff. likning: Karakteristiske løsningen har ingen reel løsning

Frie svingninger